五一 DAY 5

 五一  DAY 5

---

       V  点  1----n

       E  边 

/*
Given a graph with N nodes and M unidirectional edges.
Each edge e_i starts from u_i to v_i and weights w_i
Output a travelsal from node 1 and output degree of each node.

给出了一个具有n个节点和m个单向边的图。
每边E_i从U_i开始到V_i，重量W_i
从节点1输出一个航迹，输出每个节点的度数。
*/
#include <bits/stdc++.h>

using namespace std;

const int N = 5005;

int ideg[N], odeg[N], n, m, edg[N][N];
bool visited[N];

void travel(int u, int distance)
{
    cout << u << " " << distance << endl; visited[u] = true;
    for (int v = 1; v <= n; v++)
        if (edg[u][v] != -1 && !visited[v])
            travel(v, distance + edg[u][v]); //if there is an edge (u, v) and v has not been visited, then travel(v)
}
int main()
{
    cin >> n >> m;
    memset(edg, -1, sizeof edg);    //没有边 
    memset(visited, false, sizeof visited);  //没访问 
    for (int u, v, w, i = 1; i <= m; i++)
        cin >> u >> v >> w, edg[u][v] = w, odeg[u]++, ideg[v]++;   //u出度，V入度 
    for (int i = 1; i <= n; i++)
        cout << ideg[i] << " " << odeg[i] << endl;
    for (int i = 1; i <= n; i++)
        if (!visited[i]) travel(i, 0);
}

 

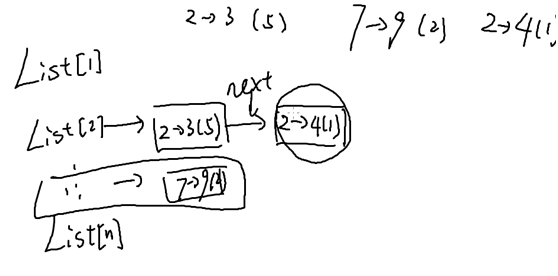
 数组版本：

/*
Given a graph with N nodes and M unidirectional edges.
Each edge e_i starts from u_i to v_i and weights w_i
Output a travelsal from node 1 and output degree of each node.

给出了一个具有n个节点和m个单向边的图。
每边E_i从U_i开始到V_i，重量W_i
从节点1输出一个航图，输出每个节点的度数。
*/
#include <bits/stdc++.h>

using namespace std;

const int N = 5005;

struct edge {
    int u, v, w; edge *next;
    edge(int _u, int _v, int _w, edge *_next):
        u(_u), v(_v), w(_w), next(_next) {}
};
edge *head[N]; //List[u] stores all edges start from u  最前面节点 
int ideg[N], odeg[N], n, m;
bool visited[N];

void add(int u, int v, int w)
{
    edge *e = new edge(u, v, w, head[u]);
    head[u] = e;
}
void travel(int u, int distance)
{
    cout << u << " " << distance << endl; visited[u] = true;
    for (edge *e = head[u]; e ; e = e -> next)
        if (!visited[e -> v])
            travel(e -> v, distance + e -> w); //if there is an edge (u, v) and v has not been visited, then travel(v)
}
int main()
{
    cin >> n >> m;
    memset(visited, false, sizeof visited);
    memset(head, 0, sizeof head);
    for (int u, v, w, i = 1; i <= m; i++)
        cin >> u >> v >> w, add(u, v, w), odeg[u]++, ideg[v]++;
    for (int i = 1; i <= n; i++)
        cout << ideg[i] << " " << odeg[i] << endl;
    for (int i = 1; i <= n; i++)
        if (!visited[i]) travel(i, 0);
}

 指针版本：

Head   ：   边的编号

 

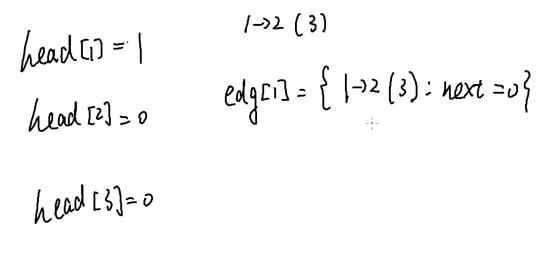
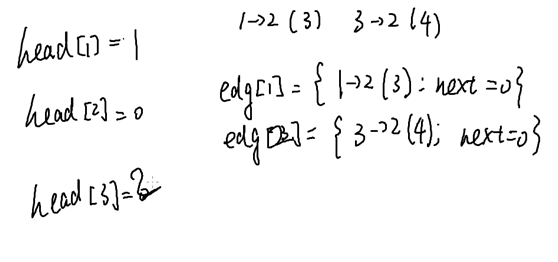
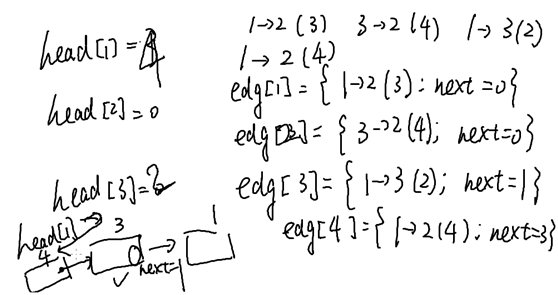
#include <bits/stdc++.h>

using namespace std;

const int N = 5005;

struct edge {
    int u, v, w, next;
}edg[N];

int head[N]; //List[u] stores all edges start from u
int ideg[N], odeg[N], n, m, cnt; //cnt: numbers of edges
bool visited[N];

void add(int u, int v, int w)
{
    int e = ++cnt;
    edg[e] = (edge){u, v, w, head[u]};
    head[u] = e;
}
void travel(int u, int distance)
{
    cout << u << " " << distance << endl; visited[u] = true;
    for (int e = head[u]; e ; e = edg[e].next)
        if (!visited[edg[e].v])
            travel(edg[e].v, distance + edg[e].w); //if there is an edge (u, v) and v has not been visited, then travel(v)
}
int main()
{
    cin >> n >> m; cnt = 0;
    memset(visited, false, sizeof visited);
    memset(head, 0, sizeof head);
    for (int u, v, w, i = 1; i <= m; i++)
        cin >> u >> v >> w, add(u, v, w), odeg[u]++, ideg[v]++;
    for (int i = 1; i <= n; i++)
        cout << ideg[i] << " " << odeg[i] << endl;
    for (int i = 1; i <= n; i++)
        if (!visited[i]) travel(i, 0);
}

/*
Given a graph with N nodes and M unidirectional edges.
Each edge e_i starts from u_i to v_i and weights w_i
Output a travelsal from node 1 and output degree of each node.
*/

 

和传统二维数组相比，可以防止浪费，用多少开多少

#include <bits/stdc++.h>

using namespace std;

const int N = 5005;

struct edge {
    int u, v, w;
};
//vector<edge> edg;   //edg是变长数组 
vector<edge> edg[N];   //n个变长数组 
int ideg[N], odeg[N], n, m, cnt; //cnt: numbers of edges
bool visited[N];

void add(int u, int v, int w)
{
    edg[u].push_back((edge){u, v, w});//(edge){u, v, w}强制类型转化 
}
void travel(int u, int distance)
{
    cout << u << " " << distance << endl; visited[u] = true;
    for (int e = 0; e < edg[u].size(); e++)
        if (!visited[edg[u][e].v]) //以u出发的第e条出边 
            travel(edg[u][e].v, distance + edg[u][e].w); //if there is an edge (u, v) and v has not been visited, then travel(v)
}
int main()
{
    cin >> n >> m; cnt = 0;
    memset(visited, false, sizeof visited);
    for (int u, v, w, i = 1; i <= m; i++)
        cin >> u >> v >> w, add(u, v, w), odeg[u]++, ideg[v]++;
    for (int i = 1; i <= n; i++)
        cout << ideg[i] << " " << odeg[i] << endl;
    for (int i = 1; i <= n; i++)
        if (!visited[i]) travel(i, 0);
}

/*
Given a graph with N nodes and M unidirectional edges.
Each edge e_i starts from u_i to v_i and weights w_i
Output a travelsal from node 1 and output degree of each node.
*/

     MST问题

也就是保留点，删除边（不一定每个点都要留下）

生成树不唯一，数量是指数级别

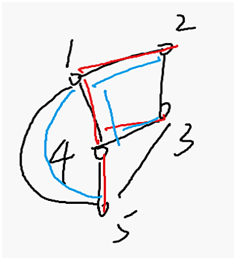
蓝色的边和点构成一个生成树

红色的边和点构成一个生成树

 

瓶颈生成树

 

显然红色的树更合题意

所以此处可以用到并查集

 

最常用

把边拿掉，一点一点加进去

判断是否连通，并查集

为什么克鲁斯卡尔是对的

反正最后还是要吧a,v，连起来，早连接，权值小

严谨证明：

消圈算法（麻烦，不用）

假设原图有个圈

不断断开权值最大边

剩下的就是最小生成树

#include <bits/stdc++.h>

using namespace std;

const int maxn = 1000005;
struct edge {
    int u, v, w;
}edg[maxn];
int n, m, p[maxn], ans = 0;

bool cmp(edge a, edge b)  //小到大 
    {return a.w < b.w;}
int findp(int t) 
    {return p[t] ? p[t] = findp(p[t]) : t;}
bool merge(int u, int v)
{
    u = findp(u); v = findp(v);
    if (u == v) return false;
    p[u] = v; return true;
}
int main()
{
    cin >> n >> m;
    for (int i = 1, u, v, w; i <= m; i++)
        cin >> u >> v >> w, edg[i] = (edge){u, v, w};  
    sort(edg + 1, edg + m + 1, cmp);
    
    for (int i = 1; i <= m; i++)
        if (merge(edg[i].u, edg[i].v))  //并茶几 
            ans = max(ans, edg[i]. w);
    cout << ans << endl;
}

 Prim 

有些麻烦

先选择一号点，所有出边中最小的，联通，

然后找距离连通块最近的点，联通

总结： 先选择一号点，找出与当前联通快最小的边

（一个联通快，不断扩大）

Kosaraju

N个连通块，不断合并

第一轮每个连通块找到与他相连的最小边

（用堆优化）

 给出一张图

简单路径：不经过重复的点

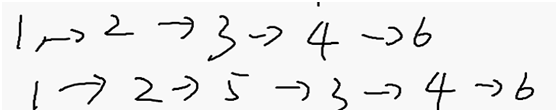
鬼畜路径：可以转圈圈

路径的长度:

路径中所有边，边权值和

  SSP

 

 

用中心点更新最短路

#include <bits/stdc++.h>

using namespace std;

const int N = 505;
const int inf = 1 << 29;

int d[N][N], n, m;       //邻接矩阵存图
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
        {
          if(i==j) d[i][j]=0;  //d[i][i]应该为0 ，我到我自己 
          else  d[i][j]=inf;
        } //初始化无穷大 
         
    for (int u, v, w, i = 1; i <= m; i++)
        cin >> u >> v >> w, d[u][v] = min(d[u][v], w); //处理重边 

    for (int k = 1; k <= n; k++)     
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
    //必须先枚举中间点 
    
    //可以求出任意两点间的最短路径 
}

 

    

 

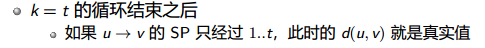
一般来说题目只能做n<=500

结束后枚举d[u][u]如果有负数，证明有负权环

 

Floyd不可以处理负权环，但是可以判定有无

 

[代码]：

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;
const int inf = 1 << 29;

struct edge{
    int u, v, w;
}edg[N];
int d[N], n, m, S;
int main()
{
    cin >> n >> m >> S;
    for (int i = 1; i <= n; i++) d[i] = inf;
    for (int u, v, w, i = 1; i <= m; i++)
        cin >> u >> v >> w, edg[i] = (edge){u, v, w};
        
    d[S] = 0;
    for (int i = 1; i <= n; i++)      //n点 
        for (int j = 1; j <= m; j++)  //枚举m条边 
        {
            int u = edg[j].u, v = edg[j].v, w = edg[j].w;
            d[v] = min(d[v], d[u] + w);
        }
}

其实是bellman-ford的队列优化版

对比bellman-ford

 

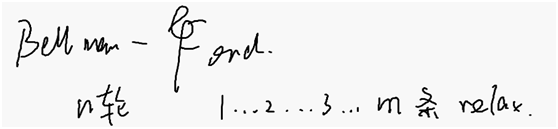
一共n个点，全局松弛，把所有边都松弛一遍

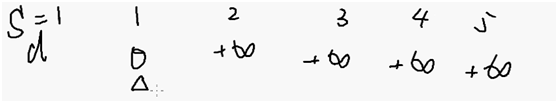
假设点1可以更新点3，点5，

第一次全局更新的时候没有把2，4 更新的更小，下一轮也不用更新他了，否则就是重复计算

 

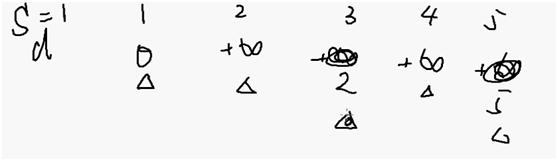
由于3，5被更新的更小，所以他们的出边继续更新才有机会把下面的点最短路径更新的更小

 

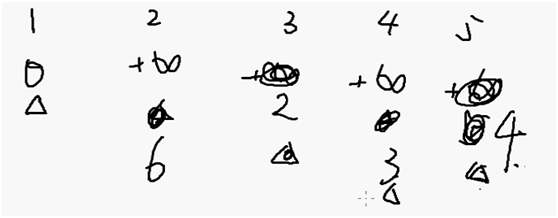
      但是Spfa 会被网格图卡的很慢

 

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;
const int inf = 1 << 29;

struct edge{      //邻接表 
    int u, v, w;
};
vector<edge> edg[N];
int d[N], n, m, S;  //d是答案 

queue<int> Queue;  
bool inQueue[N];
int cntQueue[N];

void add(int u, int v, int w)
{
    edg[u].push_back((edge){u, v, w});
}
int main()
{
    cin >> n >> m >> S;
    for (int i = 1; i <= n; i++) d[i] = inf;
    for (int u, v, w, i = 1; i <= m; i++)
        cin >> u >> v >> w, add(u, v, w);
        
    d[S] = 0; inQueue[S] = true; Queue.push(S); //放进s点 
    while (!Queue.empty())
    {
        int u = Queue.front(); Queue.pop(); inQueue[u] = false;
        for (int e = 0; e < edg[u].size(); e++)
        {
            int v = edg[u][e].v, w = edg[u][e].w;
            if (d[v] > d[u] + w)
            {
                d[v] = d[u] + w;
                if (!inQueue[v])
                {
                    Queue.push(v); ++cntQueue[v]; inQueue[v] = true;
                    if (cntQueue[v] >= n) {cout << "Negative Ring" << endl; return 0;} //发现负权环 
                }
            }
        }
    }
    for (int i = 1; i <= n; i++)
        cout << d[i] << endl;
}

 

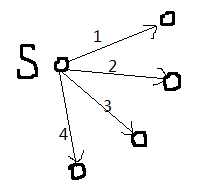
用起点松弛其余点，假设点 1 是距离S最近的点，找到这个点之后就用它再来更新下面的点

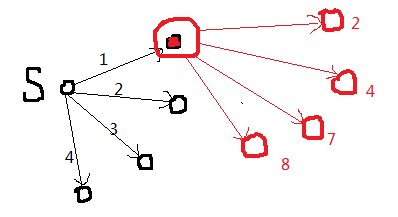
then,不管S和点1 ，找到d最小的点2 更新，它的 d是真实值

         因为它已经被更新过了，而且外边的点的边权都比它大

 

 

[代码]：

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;
const int inf = 1 << 29;

struct edge{
    int u, v, w;
};
vector<edge> edg[N];
int d[N], n, m, S;

bool relaxed[N];   //表示一个元素是否在队列 
/*struct Qnode {
    int u, du;
    bool operator<(const Qnode &v)
        const {return v.du < du;}
};
priority_queue<Qnode> PQueue;
*/
void add(int u, int v, int w)
{
    edg[u].push_back((edge){u, v, w});
}
int main()
{
    cin >> n >> m >> S;
    for (int i = 1; i <= n; i++) d[i] = inf;   
    for (int u, v, w, i = 1; i <= m; i++)
        cin >> u >> v >> w, add(u, v, w);
        
    d[S] = 0;
    for (int i = 1; i <= n; i++)
    {
        int u = 1; while (relaxed[u]) ++u;
        for (int j = 1; j <= n; j++)
            if (!relaxed[j] && d[j] < d[u]) u = j;
        //find a node u not relaxed yet with smallest d(u)
        //寻找第一个不在队列里的 d最小的u 
        relaxed[u] = true;
        for (int e = 0; e < edg[u].size(); e++)
        {
            int v = edg[u][e].v, w = edg[u][e].w;
            d[v] = min(d[v], d[u] + w);
        }
    }
    for (int i = 1; i <= n; i++)
        cout << d[i] << endl;
}

 [堆优化Dijkstra]:

//加优化 
#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;
const int inf = 1 << 29;

struct edge{
    int u, v, w;
};
vector<edge> edg[N];
int d[N], n, m, S;

bool relaxed[N];
struct Qnode {     //堆里元素 
    int u, du;
    bool operator<(const Qnode &v)    //const不能少 
        const {return v.du < du;}    //小的在队顶 
};
priority_queue<Qnode> PQueue;      //优先队列 

void add(int u, int v, int w)
{
    edg[u].push_back((edge){u, v, w});
}
int main()
{
    cin >> n >> m >> S;
    for (int i = 1; i <= n; i++) d[i] = inf;
    for (int u, v, w, i = 1; i <= m; i++)
        cin >> u >> v >> w, add(u, v, w);
        
    d[S] = 0; PQueue.push((Qnode){S, 0});  //需要更新的点 
    while (!PQueue.empty())
    {
        int u = PQueue.top().u; PQueue.pop();  //对不为空 
        if (relaxed[u]) continue;   //松弛过就不松 
            //if edges staring from u are already relaxed, no need to relax again.
        relaxed[u] = true;     //打标机 
        for (int e = 0; e < edg[u].size(); e++)  //枚举出边 
        {
            int v = edg[u][e].v, w = edg[u][e].w; //u v 是w的出边 
            if (d[v] > d[u] + w)
            {
                d[v] = d[u] + w;
                PQueue.push((Qnode){v, d[v]});   
                //if d(v) is updated, push v into PQueue
            }
        }
    }
    for (int i = 1; i <= n; i++)
        cout << d[i] << endl;
}

 

 将有向图的所有的有向边替换为无向边，所得到的图称为原图的基图。如果一个有向图的基图是连通图，则有向图是弱连通图。

找拓扑序的方法：

１．找出度为０ 的点，放在拓扑序列最后面，指向该点的边删掉，与所删除的边起点出度数－１

２．重复以上操作，得出拓扑序

结论1　有拓扑序一定是DAG

结论2   任意DAG一定有拓扑序

           任意DAG一定有出度为０的点，否则有环，

          出度为０的点放在拓扑序最后

          把这个点和他的入度边删去，图还是个DAG

          同上操作，做完后就是拓扑序

 

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;
const int inf = 1 << 29;

struct edge{
    int u, v;
};
vector<edge> edg[N];
int n, m, outdeg[N], ans[N];

queue<int> Queue;   //出度为0 
void add(int u, int v)
{
    edg[u].push_back((edge){u, v});
}
int main()
{
    cin >> n >> m;
    for (int u, v, i = 1; i <= m; i++)
        cin >> u >> v, add(v, u), outdeg[u]++; //找入度，倒着记录 
        
    for (int i = 1; i <= n; i++)
        if (outdeg[i] == 0) Queue.push(i);
    for (int i = 1; i <= n; i++)
    {
        if (Queue.empty())
            {printf("Not DAG"); return 0;}
        int u = Queue.front(); Queue.pop(); ans[n - i + 1] = u; //倒着 
        for (int e = 0; e < edg[u].size(); e++) //指向u的边删掉 
        {
            int v = edg[u][e].v;  //指向u的点 出度减少 
            if (--outdeg[v] == 0) //先自减，再使用 
               Queue.push(v);
        }
    }
}

ｐｒｏ１   

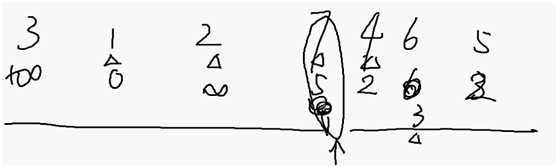
考虑DAG上找单元最短路

１到不了３

１松弛出边７　５　出边肯定在自己后边

然后出边在更新自己出边，直达完成

自己被更新完就不能被改变了，他要继续更新自己出边

 

ｐｒｏ　２

考虑DAG求拓扑排序数量

（做不到）

  

LCA（写在这里啦）

 

     

 

 ans=len(x)-len(t)+len(y)+len(t)

       =len(x)+len(y)-2*len(t)