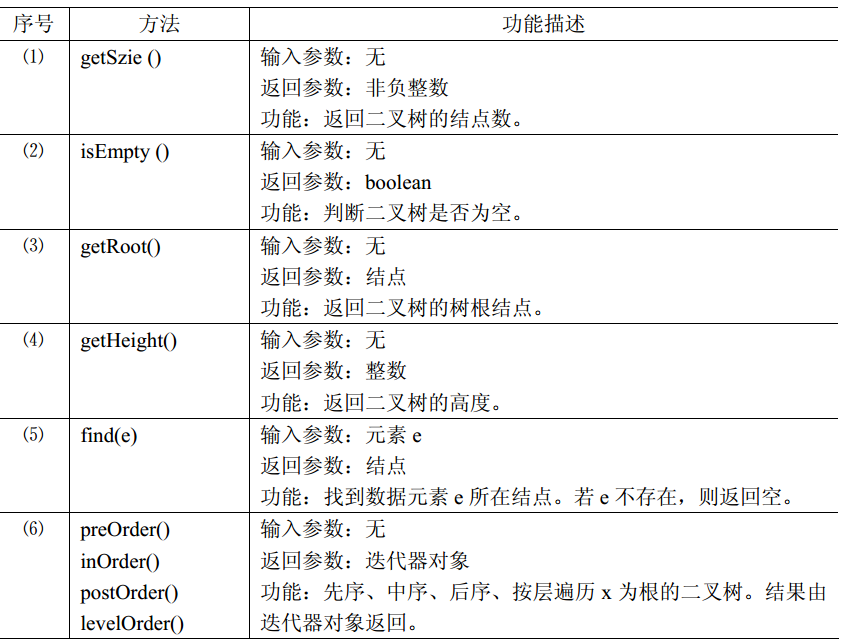
一、二叉树介绍
因为任何树都可以转化为二叉树进行处理,并且二叉树适合计算机的存储和处理,因此在数据结构中二叉树是研究的重点。
每个结点的度均不超过 2 的有序树,称为二叉树( binary tree)。
与树的递归定义类似,二叉树的递归定义如下:二叉树或者是一棵空树,或者是一棵由一个根结点和两棵互不相交的分别称为根的左子树和右子树的子树所组成的非空树。
由以上定义可以看出,二叉树中每个结点的孩子数只能是 0、 1 或 2 个,并且每个孩子都有左右之分。位于左边的孩子称为左孩子,位于右边的孩子称为右孩子;以左孩子为根的子树称为左子树,以右孩子为根的子树称为右子树。
与树的基本操作类似,二叉树有如下基本操作:
二、 二叉树的性质
在二叉树中具有以下重要性质:
![]()
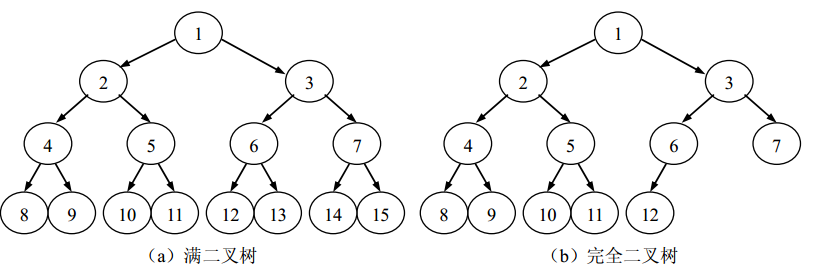
下面介绍两种特殊的二叉树,然后讨论其有关性质。

可以对满二叉树的结点进行编号,约定编号从根结点起,层间自上而下,层内自左而右,逐层由 1 到 n 进行标号。
![]()
如果按照上述对满二叉树结点编号的方法,对具有 n 个结点的完全二叉树中结点进行编号,那么完全二叉树中 1~ n 号结点的位置与满二叉树中 1~ n 号结点的位置是一致的。图 ( b)所示的二叉树就是一棵完全二叉树。可见,满二叉树必为完全二叉树,而完全二叉树不一定是满二叉树。

三、二叉树遍历
所谓树的遍历( traversal),就是按照某种次序访问树中的所有结点,且每个结点恰好访问一次。也就是说,按照被访问的次序,可以得到由树中所有结点排成的一个序列。树的遍历也可以看成是人为的将非线性结构线性化。这里的“访问”是广义的,可以是对结点作各种处理,例如输出结点信息、更新结点信息等。在我们的实现中,并不真正的“访问”这些结点,而是得到一个结点的线性序列,以线性表的形式输出。
回顾二叉树的定义,我们知道二叉树可以看成是由三个部分组成的:一个根结点、根的左子树和根的右子树。因此如果能够遍历这三部分,则可以遍历整棵二叉树。如果用 L、 D、R 分别表示遍历左子树、访问根结点、遍历右子树。那么对二叉树的遍历次序就可以有 6 种方案:
⑴ 遍历左子树,访问根,遍历右子树( LDR)
⑵ 遍历左子树,遍历右子树,访问根( LRD)
⑶ 访问根,遍历左子树,遍历右子树( DLR)
⑷ 访问根,遍历右子树,遍历左子树( DRL)
⑸ 遍历右子树,遍历左子树,访问根( RLD)
⑹ 遍历右子树,访问根,遍历左子树( RDL)
在上述 6 种遍历方案中,如果规定对左子树的遍历先于对右子树的遍历,那么还剩下 3种情况: DLR、 LDR、 LRD。根据对根访问的不同顺序,分别称 DLR 为先根(序)遍历,LDR 为中根(序)遍历, LRD 为后根(序)遍历。为了方便理解,可以记忆成先根遍历,中根遍历和后根遍历。
请注意,这里的先序遍历、中序遍历、后序遍历是递归定义的,即在左右子树中也是按相应的规律进行遍历。下面给出三种遍历方法的递归定义。
⑴ 先序遍历( DLR)二叉树的操作定义为:
若二叉树为空,则空操作;否则
① 访问根结点;
② 先序遍历左子树;
③ 先序遍历右子树。
⑵ 中序遍历( LDR)二叉树的操作定义为:
若二叉树为空,则空操作;否则
① 中序遍历左子树;
② 访问根结点;
③ 中序遍历右子树。
⑶ 后序遍历( LRD)二叉树的操作定义为:
若二叉树为空,则空操作;否则
① 后序遍历左子树;
② 后序遍历右子树;
③ 访问根结点。
四、代码实现
由于二叉树就是一个子节点数为2的这么一棵树,那么只需要在前面树的代码实现中简单的改一下,就是一颗二叉树了。前面树结点定义的时候,它的子结点定义的是一个list,那么二叉树只需将它的长度限制为2,那这不就是二叉树了吗?访问子结点的时候,list[0]代表左子结点,list[1]代表右子结点。