图的表示及代码实现

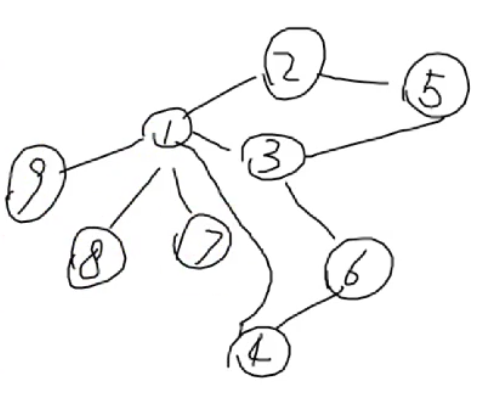
一、图的表示

　　从图的逻辑结构定义来看，无法将图中的顶点排列成一个唯一的线性序列。在图中任意一个顶点都可以看成是图的第一个顶点，对任何一个顶点而言，它的邻接点之间也不存在顺序关系。为了方便存储和操作，需要将图中的顶点按一定的序列排列起来。

　　顶点在图中的位置就是指该顶点在人为确定的序列中的位置。

　　由于图的结构比较复杂，任意两个顶点之间都可能存在联系，因此无法以数据元素在存储区的位置来表示元素之间的关系，即图没有顺序映像的存储结构，但可以借助数组来表示数据元素之间的关系。

　　借助数组存储的方法有邻接矩阵表示法和邻接表表示法，边集表示法。

1．邻接矩阵表示法

1>定义

　　图的邻接矩阵（adjacent matrix）表示法是使用数组来存储图结构的方法，也被称为数组表示法。 它采用两个数组来表示图：一个是用于存储所有顶点信息的一维数组，另一个是用于存储图中顶点之间关联关系的二维数组，这个关联关系数组也被称为邻接矩阵。

　　

　　

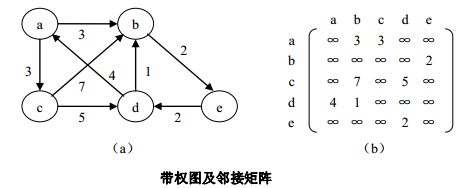
2>性质

邻接矩阵有如下特性：

• （1）图中各顶点序号确定后，图的邻接矩阵是唯一确定的。
• （2）无向图和无向网的琳姐矩阵是一个对称矩阵。
• （3）无向图邻接矩阵中第i行或第i列的非0元素个数即为第i个顶点的度。
• （4）有向图邻接矩阵第i行非0元素个数为第i个顶点的出度，第i列非0元素个数为第i个顶点的入度，第i个顶点的度为第i行与第i列非0元素个数之和。
• （5）无向图的边数等于邻接矩阵中非0元素个数之和的一半，有向图的弧数等于邻接矩阵中非0元素个数之和。

3>优缺点

优点：

邻接矩阵表示法对于以图的顶点为主的运算比较适合。

缺点：

除完全图外，其他图的邻接矩阵有许多零元素，特别是当n值较大，而边数相对完全图的边n-1又少的多时，则此矩阵称为稀疏矩阵，非常浪费存储空间。

3>表示

　　

2．邻接表表示法

　　邻接表（adjacency list）是图的一种链式存储方法，邻接表表示法类似于树的孩子链表表示法。

　　在邻接表中对于图G中的每个顶点vi建立一个单链表，将所有邻接于vi的顶点vj链成一个单链表，并在表头附设一个表头结点，这个单链表就称为顶点vi的邻接表。

1>结点

　　邻接表中共有两种结点结构，分别是边表结点和表头结点。

　　

邻接表中的每一个结点均包含有两个域：邻接点域和指针域。

• 邻接点域用于存放与定点vi相邻接的一个顶点的序号。
• 指针域用于指向下一个边表结点。

边表结点由3个域组成：

• 邻接点域（adjvex）指示与定点vi邻接的顶点在图中的位置。
• 链域（nextdge）指向下一条边所在的结点。
• 数据域（info）存储和边有关的信息。

头结点由2个域组成：

• 链域（firstedge）指向链表中的第一个结点之外。
• 数据域（data）存储顶点相关信息。

如下图为邻接表的存储示例：

　　

2>分类

在无向图的邻接表中，顶点的每一个边表结点对应于与顶点相关联的一条边。

在有向图的邻接表中，顶点的每一个边表结点对应于以顶点为始点的一条弧，因此也称有向图的邻接表的边表为出边表。

在有向图的邻接表中，将顶点的每个边表结点对应于以顶点为重点的一条弧，即用便捷点的邻接点域存储邻接到顶点的序号，由此构成的邻接表称为有向图的逆邻接表，逆邻接表有边表称为入边表。

3>邻接表与邻接矩阵的关系

邻接表与邻接矩阵的关系如下：

• （1）对应于邻接矩阵的每一行有一个线形连接表；
• （2）链接表的表头对应着邻接矩阵该行的顶点；
• （3）链接表中的每个结点对应着邻接矩阵中该行的一个非零元素；
• （4）对于无向图，一个非零元素表示与该行顶点相邻接的另一个顶点；
• （5）对于有向图，非零元素则表示以该行顶点为起点的一条边的终点。

邻接表表示法示例如下：

　　

4>邻接表的性质

邻接表的性质如下：

• （1）图的邻接表表示不是惟一的，它与表结点的链入次序有关。
• （2）无向图的邻接表中第i个边表的结点个数即为第i个顶点的度。
• （3）有向图的邻接表中第i个出边表的结点个数即为第i个结点的出度，有向图的逆邻接表中第i个入边表的结点个数即为第i个结点的入度。
• （4）无向图的边数等于邻接表中边表结点数的一半，有向图的弧数等于邻接表（逆邻接表）中出边表结点（入边表结点）的数目。

需要说明的是：

• （1）在邻接表的每个线性链接表中各结点的顺序是任意的。
• （2）邻接表中的各个线性链接表不说明他们顶点之间的邻接关系。
• （3）对于无向图，某顶点的度数=该顶点对应的线性链表的结点数。
• （4）对于有向图，某顶点的“出度”数=该顶点对应的线性链表的结点数；求某顶点的“入度”需要对整个邻接表的各链接扫描一遍，看有多少与该顶点相同的结点，相同结点数之和即为“入度”值。

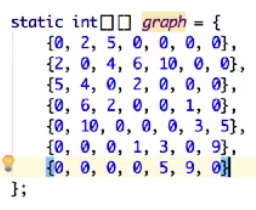
3．边集表示法

　　边集表示就是把每条边都存储起来作为一个集合。如下图所示

　　　　

　　表示的图为：

　　　　

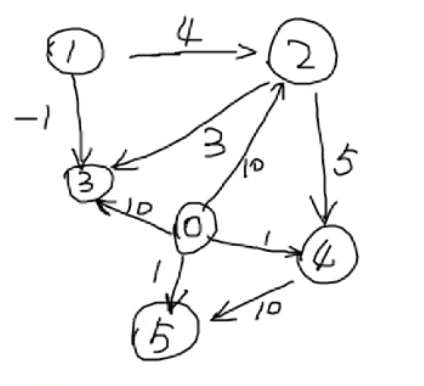
二、代码实现：

　　邻接表表示法：

import java.util.ArrayList;
import java.util.List;


/*邻接表*/
public class GraphNode_AL {
    public int val;
    private List<GraphNode_AL> neighbors;// 邻居

    public boolean checked = false;

    public GraphNode_AL(int val) {
        this.val = val;
    }

    public GraphNode_AL getNeighbor(int i) {
        return neighbors.get(i);
    }

    public void add(GraphNode_AL node) {
        if (this.neighbors == null)
            this.neighbors = new ArrayList<>();
        this.neighbors.add(node);
    }

    public int size() {
        return this.neighbors.size();
    }
}

　　Graph类：

/*邻接表来表示图*/
public class Graph {
    public static void main(String[] args) {
        GraphNode_AL n1 = new GraphNode_AL(1);
        GraphNode_AL n2 = new GraphNode_AL(2);
        GraphNode_AL n3 = new GraphNode_AL(3);
        GraphNode_AL n4 = new GraphNode_AL(4);
        GraphNode_AL n5 = new GraphNode_AL(5);
        GraphNode_AL n6 = new GraphNode_AL(6);
        GraphNode_AL n7 = new GraphNode_AL(7);
        GraphNode_AL n8 = new GraphNode_AL(8);
        GraphNode_AL n9 = new GraphNode_AL(9);

        n1.add(n2);
        n1.add(n3);
        n1.add(n7);
        n1.add(n8);
        n1.add(n9);

        n2.add(n1);
        n2.add(n5);

        n3.add(n1);
        n3.add(n5);
        n3.add(n6);

        n4.add(n1);
        n4.add(n6);
        n5.add(n2);
        n5.add(n3);
        n6.add(n3);
        n6.add(n4);
        n7.add(n1);
        n8.add(n1);
        n9.add(n1);

        dfs(n9);

    }

    static void dfs(GraphNode_AL node) {
        System.out.println(node.val);
        node.checked = true;
        for (int i = 0; i < node.size(); i++) {
            GraphNode_AL graphNode = node.getNeighbor(i);
            if (graphNode.checked == false)
                dfs(graphNode);
        }
    }
}

　　表示的图为：