问题是这样子的:
输入是具有n个浮点数的向量x,输出是输入向量的任何子向量中的最大和。
本文部分参考自一博文。
对于这道题,作者给出了总共4种不同方法:
1. 直接解法
最直接的方式是遍历所有可能的连续子向量,用i和j分别表示向量的首元和最后的尾元,k表示真实的尾元:
1 int maxsum1(int * arr, int len) 2 { 3 assert(len > 0); 4 int maxsofar = 0; 5 int sum = 0; 6 for (int i = 0; i < len; i++) 7 { 8 for (int j = i; j < len; j++) 9 { 10 sum = 0; 11 for (int k = i; k < j + 1; k++) 12 { 13 sum += *(arr + k); 14 } 15 maxsofar = max(maxsofar, sum); 16 } 17 } 18 return maxsofar; 19 }
2. O(n2)的解法
第1种方法的代码具有显而易见的浪费:对于一个子序列可能重复计算了多次。并且具有O(n3)的时间复杂度。其实k是多余的,依靠首尾两个变量i、j足以表示一个子向量。同时,j增长时,可以直接使用上一次的计算和与新增元素相加。因此改写为:
1 int maxsum2(int * arr, int len) 2 { 3 assert(len > 0); 4 int maxsofar = 0; 5 int sum = 0; 6 for (int i = 0; i < len; i++) 7 { 8 sum = 0; 9 for (int j = i; j < len; j++) 10 { 11 sum += *(arr + j); 12 maxsofar = max(maxsofar, sum); 13 } 14 } 15 return maxsofar; 16 }
另外一方面,由这个避免重复计算累加和的角度出发,构造一个累加和数组cumarr,cumarr[i]表示array[0...i]各个数的累加和,这样,array[i...j]的和就可以用cumarr[j]-cumarr[i-1]来表示了。考虑到边界值,令cumarr[-1]=0。在C/C++中的做法是令cumarr指向一个数组的第1个元素,cumarr = recumarr +1。有了cumarr[]就可以遍历所有的i、j来求最大值了:
1 int maxsum3(int * arr, int len) 2 { 3 assert(len > 0); 4 int maxsofar = 0; 5 int sum = 0; 6 int * cumarr = new int[len + 1]; 7 cumarr[0] = 0; 8 for (int i = 0; i < len; i++) 9 { 10 cumarr[i + 1] = cumarr[i] + *(arr + i); 11 } 12 13 for (int i = 0; i < len; i++) 14 { 15 for (int j = i; j < len; j++) 16 { 17 sum = cumarr[j + 1] - cumarr[i]; 18 maxsofar = max(maxsofar, sum); 19 } 20 } 21 22 delete cumarr; 23 return maxsofar; 24 }
虽然这个累加和数组的解法与后面两个相比,时间复杂度远不是最优的,然而这种数据结构很有用。
累积表这种想法值得注意!
3. 分治法(nlogn)
分治法的基本思想是,把n个元素的向量分成两个n/2的子向量,递归地解决问题再把答案合并。
分容易,合并就要花点心思了。因为对于初始大小为n的向量,它的最大连续子向量可能整体在分成的两个子向量中之一,也可能跨越了两个子向量。每次合并都需要计算这个跨越分界点的最大连续子向量,占据了很大的开销。
1 int maxsum4(int * arr, int len) 2 { 3 assert(len > 0); 4 int maxsofar = 0; 5 if (len == 1) 6 { 7 maxsofar = arr[0]; 8 } 9 else 10 { 11 int sum = 0; 12 int l = 0; 13 int u = len - 1; 14 int m = (l + u) / 2; 15 16 // find max crossing to left 17 int lmax = 0; 18 for (int i = m; i >= 0; i--) 19 { 20 sum += *(arr + i); 21 lmax = max(lmax, sum); 22 } 23 24 // find max crossing to right 25 int rmax = 0; 26 sum = 0; 27 for (int i = m + 1; i <= u; i++) 28 { 29 sum += *(arr + i); 30 rmax = max(rmax, sum); 31 } 32 33 maxsofar = max(lmax + rmax, maxsum4(arr, m + 1), maxsum4(arr + m + 1, u - m)); 34 } 35 36 return maxsofar; 37 }
延伸:分治法的最坏情况讨论
根据合并过程,如果每次的最长子向量都恰好位于边界,即下图中灰色部分,两者其中之一:
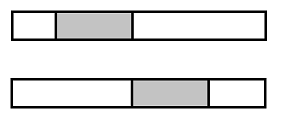
结果导致每次合并时都重复计算了在左边和右边的最长子向量,相当的浪费。解决方法是返回值中给出边界,如果边界在分界点上,合并时就不需要重复计算了。
4. 扫描算法
从头到尾扫描数组,扫描至array[i]时,可能的最长子向量有两种情况:要么在前i-1个元素中,要么以i结尾。前者的大小记为maxsofar,后者记为maxendinghere。
1 int maxsum5(int * arr, int len) 2 { 3 assert(len > 0); 4 int maxsofar = 0; 5 int maxendinghere = 0; 6 for (int i = 0; i < len; i++) 7 { 8 maxendinghere = max(maxendinghere + *(arr + i), 0); 9 maxsofar = max(maxsofar, maxendinghere); 10 } 11 return maxsofar; 12 }
这个算法可以看做是动态规划,把长度为n的数组化成了递归的子结构,并从首开始扫描求解。时间复杂度只有O(n)。
注:直到最近做到LeetCode的题目,才发现这个扫描算法并不适用于存在负数的数组。对于存在负数的数组,可用下述解法:
1 int maxSubArray(vector<int>& nums) { 2 int sz = nums.size(); 3 if(sz == 0) 4 return 0; 5 6 int maxsofar = INT_MIN; 7 int sum = 0; 8 for(int i = 0; i < sz; i++) 9 { 10 sum += nums[i]; 11 if(sum > maxsofar) 12 maxsofar = sum; 13 if(sum < 0) 14 sum = 0; 15 } 16 17 return maxsofar; 18 }
同样的,利用该算法,我们还可以求总共最小的连续子向量:
1 int minsum(int * arr, int len) 2 { 3 assert(len > 0); 4 int minsofar = 0; 5 int minendinghere = 0; 6 for (int i = 0; i < len; i++) 7 { 8 minendinghere = min(minendinghere + *(arr + i), 0); 9 minsofar = min(minsofar, minendinghere); 10 } 11 12 return minsofar; 13 }
附整个程序:

1 #include <iostream> 2 #include <stdlib.h> 3 #include <cassert> 4 using namespace std; 5 6 int max(int a, int b); 7 int max(int a, int b, int c); 8 int min(int a, int b); 9 10 int maxsum1(int * arr, int len); 11 int maxsum2(int * arr, int len); 12 int maxsum3(int * arr, int len); 13 int maxsum4(int * arr, int len); 14 int maxsum5(int * arr, int len); 15 16 int minsum(int * arr, int len); 17 18 int main() 19 { 20 int arr[8] = {5, -2, -3, 4, -2, -8, 10, -5}; 21 int len = sizeof(arr) / sizeof(int); 22 23 int maxsofar1 = maxsum1(arr, len); 24 cout << "Maxsofar1 = " << maxsofar1 << endl; 25 26 int maxsofar2 = maxsum2(arr, len); 27 cout << "Maxsofar2 = " << maxsofar2 << endl; 28 29 int maxsofar3 = maxsum3(arr, len); 30 cout << "Maxsofar3 = " << maxsofar3 << endl; 31 32 int maxsofar4 = maxsum4(arr, len); 33 cout << "Maxsofar4 = " << maxsofar4 << endl; 34 35 int maxsofar5 = maxsum5(arr, len); 36 cout << "Maxsofar5 = " << maxsofar5 << endl; 37 38 int minsofar = minsum(arr, len); 39 cout << "Minsofar = " << minsofar << endl; 40 41 return 0; 42 } 43 44 int max(int a, int b) 45 { 46 return (a > b) ? a : b; 47 } 48 49 int max(int a, int b, int c) 50 { 51 int temp = max(a, b); 52 return (temp > c) ? temp : c; 53 } 54 55 int min(int a, int b) 56 { 57 return (a < b) ? a : b; 58 } 59 60 int maxsum1(int * arr, int len) 61 { 62 assert(len > 0); 63 int maxsofar = 0; 64 int sum = 0; 65 for (int i = 0; i < len; i++) 66 { 67 for (int j = i; j < len; j++) 68 { 69 sum = 0; 70 for (int k = i; k < j + 1; k++) 71 { 72 sum += *(arr + k); 73 } 74 maxsofar = max(maxsofar, sum); 75 } 76 } 77 return maxsofar; 78 } 79 80 int maxsum2(int * arr, int len) 81 { 82 assert(len > 0); 83 int maxsofar = 0; 84 int sum = 0; 85 for (int i = 0; i < len; i++) 86 { 87 sum = 0; 88 for (int j = i; j < len; j++) 89 { 90 sum += *(arr + j); 91 maxsofar = max(maxsofar, sum); 92 } 93 } 94 return maxsofar; 95 } 96 97 int maxsum3(int * arr, int len) 98 { 99 assert(len > 0); 100 int maxsofar = 0; 101 int sum = 0; 102 int * cumarr = new int[len + 1]; 103 cumarr[0] = 0; 104 for (int i = 0; i < len; i++) 105 { 106 cumarr[i + 1] = cumarr[i] + *(arr + i); 107 } 108 109 for (int i = 0; i < len; i++) 110 { 111 for (int j = i; j < len; j++) 112 { 113 sum = cumarr[j + 1] - cumarr[i]; 114 maxsofar = max(maxsofar, sum); 115 } 116 } 117 118 delete cumarr; 119 return maxsofar; 120 } 121 122 int maxsum4(int * arr, int len) 123 { 124 assert(len > 0); 125 int maxsofar = 0; 126 if (len == 1) 127 { 128 maxsofar = arr[0]; 129 } 130 else 131 { 132 int sum = 0; 133 int l = 0; 134 int u = len - 1; 135 int m = (l + u) / 2; 136 137 // find max crossing to left 138 int lmax = 0; 139 for (int i = m; i >= 0; i--) 140 { 141 sum += *(arr + i); 142 lmax = max(lmax, sum); 143 } 144 145 // find max crossing to right 146 int rmax = 0; 147 sum = 0; 148 for (int i = m + 1; i <= u; i++) 149 { 150 sum += *(arr + i); 151 rmax = max(rmax, sum); 152 } 153 154 maxsofar = max(lmax + rmax, maxsum4(arr, m + 1), maxsum4(arr + m + 1, u - m)); 155 } 156 157 return maxsofar; 158 } 159 160 int maxsum5(int * arr, int len) 161 { 162 assert(len > 0); 163 int maxsofar = 0; 164 int maxendinghere = 0; 165 for (int i = 0; i < len; i++) 166 { 167 maxendinghere = max(maxendinghere + *(arr + i), 0); 168 maxsofar = max(maxsofar, maxendinghere); 169 } 170 return maxsofar; 171 } 172 173 int minsum(int * arr, int len) 174 { 175 assert(len > 0); 176 int minsofar = 0; 177 int minendinghere = 0; 178 for (int i = 0; i < len; i++) 179 { 180 minendinghere = min(minendinghere + *(arr + i), 0); 181 minsofar = min(minsofar, minendinghere); 182 } 183 184 return minsofar; 185 }
课后相关习题
10. 假设我们想要查找的是总和最接近0的子向量,而不是具有最大总和的子向量。你能设计出的最有效的算法是什么?可以应用哪些算法设计技术?如果我们希望查找总和最接近某一给定实数t的子向量,结果又将怎样?
法一:利用累积表。我们定义cumarr[i]=arr[0]+arr[0]+...+arr[i]。如果有arr[l]=arr[u](l != u),则l..u之间的元素(不包括第l、u元素)总和为0。这个就也能够拓展到查找总和接近某一给定实数t的子向量。
法二:如果我们不考虑子向量一定要连续这个要求,我们可以先将原向量按升序进行排序,再求cumarr向量。如果cumarr[i]=0,则表示0..i(包括第0、i元素)为所求子向量。这个同样也能够拓展到查找总和接近某一给定实数t的子向量。
注:此题若用扫描算法来解决,问题比较多。
13. 在最大子数组问题中,给定n*n的实数数组,我们需要求出矩形子数组的最大总和。该问题的复杂度如何?
个人觉得很简单的就是把二维的降为一维的。如果是要求连续子向量,按照扫描算法就可以做到;如果不要求连续,则先按降序进行排序,很快就能够求出最大总和的子向量。
