欧拉函数

在数论，对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目（φ(1)=1）。此函数以其首名研究者欧拉命名(Euler'so totient function)，它又称为Euler's totient function、φ函数、欧拉商数等。 例如φ(10)=5，因为1,3,5,7,9均和10互质。

公式如下：

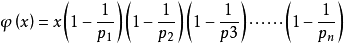
下面我写下我理解的证明过程

①对于给定的一个素数P，它φ(P) = P – 1。则对于正整数n = P^k，φ(n) =P^k – P^(k-1)。

证明：

       小于P^k的正整数有P^k – 1个，其中和P^k不互质的正整数有{P*1,P*2,......,P*(P^(k-1)-1)}共P^(k-1) – 1个。

所以φ(n) = p^k – 1 – (P^(k-1) – 1) = P^k – P(k-1)。

比如P = 7，k=2，与7^2 = 49 互质的有7*1、7*2、7*3、7*4、7*5、7*(7^1-1)这六个，即7(2-1) – 1个，所以φ(49) = 48 – 6 = 42个。

②假设q、p是互质的两个正整数，则q*p的欧拉函数是φ(q*p) = φ(q)*φ(p),gcd(q,p) = 1。

证明：

　　令n = q*p,gcd(q,p) = 1。根据孙子定理，Zn和ZqXZp之间存在一一映射，所以n的完全余数集合的元素个数等于ZqXZp集合元素的个数。

所以有φ(n) = φ(q)*φ(p)。

由于任意一个数都可以质因数分解，比如 1400 = 2^3*5*2*7。

所以任意一个数n =(X1^h1)*(X2^h2)*(X3^h3)···(Xn^hn)。

由此的φ(n) = (X1^h1-X1(h1-1))*(X2^h2-X2^(h2-1))*(X3^h3-X3^(h3-1))···(Xn^hn-Xn^(hn-1))

　　　　　  = X1^h1*X2^h2*X3^h3···Xn^hn*(1-1/X1)*(1-1/X2)*(1-1/X3)···(1-1/xn)

　　　　　  =n*(1-1/X1)*(1-1/x2)*(1-1/X3)···(1-1/Xn)

既得出结论：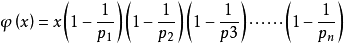

下面是我写代码：

#include <iostream>
#include <stdio.h>
#include <math.h>
using namespace std;

int euler(int n){
    int res = n, a = n;
    for(int i = 2; i <= sqrt(a); i ++){
        if(a%i==0){
            res = res/i*(i-1);
            while(a%i==0)a/=i;
        }
    }
    if(a > 1) res=res/a*(a-1);
    return res;
}
int main(){
    int n;
    cin>>n;
    cout << euler(n) << endl;
    return 0;
}