1. 插入排序
步骤:
1.从第一个元素开始,该元素可以认为已经被排序
2.取下一个元素tem,从已排序的元素序列从后往前扫描
3.如果该元素大于tem,则将该元素移到下一位
4.重复步骤3,直到找到已排序元素中小于等于tem的元素
5.tem插入到该元素的后面,如果已排序所有元素都大于tem,则将tem插入到下标为0的位置
6.重复步骤2~5
思路:
在待排序的元素中,假设前n-1个元素已有序,现将第n个元素插入到前面已经排好的序列中,使得前n个元素有序。按照此法对所有元素进行插入,直到整个序列有序。
但我们并不能确定待排元素中究竟哪一部分是有序的,所以我们一开始只能认为第一个元素是有序的,依次将其后面的元素插入到这个有序序列中来,直到整个序列有序为止。

代码如下:
void InsertSort(int* arr, int n) { for (int i = 0; i < n - 1; ++i) { //记录有序序列最后一个元素的下标 int end = i; //待插入的元素 int tem = arr[end + 1]; //单趟排 while (end >= 0) { //比插入的数大就向后移 if (tem < arr[end]) { arr[end + 1] = arr[end]; end--; } //比插入的数小,跳出循环 else { break; } } //tem放到比插入的数小的数的后面 arr[end + 1] = tem; //代码执行到此位置有两种情况: //1.待插入元素找到应插入位置(break跳出循环到此) //2.待插入元素比当前有序序列中的所有元素都小(while循环结束后到此) } }
时间复杂度:最坏情况下为O(N*N),此时待排序列为逆序,或者说接近逆序
最好情况下为O(N),此时待排序列为升序,或者说接近升序。
空间复杂度:O(1)
2.希尔排序
步骤:
1.先选定一个小于N的整数gap作为第一增量,然后将所有距离为gap的元素分在同一组,并对每一组的元素进行直接插入排序。然后再取一个比第一增量小的整数作为第二增量,重复上述操作…
2.当增量的大小减到1时,就相当于整个序列被分到一组,进行一次直接插入排序,排序完成。
思路:
希尔排序,先将待排序列进行预排序,使待排序列接近有序,然后再对该序列进行一次插入排序,此时插入排序的时间复杂度为O(N),
代码如下:
//希尔排序 void ShellSort(int* arr, int n) { int gap = n; while (gap>1) { //每次对gap折半操作 gap = gap / 2; //单趟排序 for (int i = 0; i < n - gap; ++i) { int end = i; int tem = arr[end + gap]; while (end >= 0) { if (tem < arr[end]) { arr[end + gap] = arr[end]; end -= gap; } else { break; } } arr[end + gap] = tem; } } }
时间复杂度平均:O(N^1.3)
空间复杂度:O(1)
3.选择排序
思路:
每次从待排序列中选出一个最小值,然后放在序列的起始位置,直到全部待排数据排完即可。
实际上,我们可以一趟选出两个值,一个最大值一个最小值,然后将其放在序列开头和末尾,这样可以使选择排序的效率快一倍。
代码如下:
//选择排序 void swap(int* a, int* b) { int tem = *a; *a = *b; *b = tem; } void SelectSort(int* arr, int n) { //保存参与单趟排序的第一个数和最后一个数的下标 int begin = 0, end = n - 1; while (begin < end) { //保存最大值的下标 int maxi = begin; //保存最小值的下标 int mini = begin; //找出最大值和最小值的下标 for (int i = begin; i <= end; ++i) { if (arr[i] < arr[mini]) { mini = i; } if (arr[i] > arr[maxi]) { maxi = i; } } //最小值放在序列开头 swap(&arr[mini], &arr[begin]); //防止最大的数在begin位置被换走 if (begin == maxi) { maxi = mini; } //最大值放在序列结尾 swap(&arr[maxi], &arr[end]); ++begin; --end; } }
时间复杂度:最坏情况:O(N^2)
最好情况:O(N^2)
空间复杂度:O(1)
4.冒泡排序
思路:
左边大于右边交换一趟排下来最大的在右边
代码如下:
//冒泡排序 void BubbleSort(int* arr, int n) { int end = n; while (end) { int flag = 0; for (int i = 1; i < end; ++i) { if (arr[i - 1] > arr[i]) { int tem = arr[i]; arr[i] = arr[i - 1]; arr[i - 1] = tem; flag = 1; } } if (flag == 0) { break; } --end; } }
时间复杂度:最坏情况:O(N^2)
最好情况:O(N)
空间复杂度:O(1)
5.堆排序
原文见堆排序:https://blog.csdn.net/weixin_50886514/article/details/114847405
6.快速排序
6.1 hoare版本(左右指针法)
思路:
1、选出一个key,一般是最左边或是最右边的。
2、定义一个begin和一个end,begin从左向右走,end从右向左走。(需要注意的是:若选择最左边的数据作为key,则需要end先走;若选择最右边的数据作为key,则需要bengin先走)。
3、在走的过程中,若end遇到小于key的数,则停下,begin开始走,直到begin遇到一个大于key的数时,将begin和right的内容交换,end再次开始走,如此进行下去,直到begin和end最终相遇,此时将相遇点的内容与key交换即可。(选取最左边的值作为key)
4.此时key的左边都是小于key的数,key的右边都是大于key的数
5.将key的左序列和右序列再次进行这种单趟排序,如此反复操作下去,直到左右序列只有一个数据,或是左右序列不存在时,便停止操作,此时此部分已有序
代码如下:
//快速排序 hoare版本(左右指针法) void QuickSort(int* arr, int begin, int end) { //只有一个数或区间不存在 if (begin >= end) return; int left = begin; int right = end; //选左边为key int keyi = begin; while (begin < end) { //右边选小 等号防止和key值相等 防止顺序begin和end越界 while (arr[end] >= arr[keyi] && begin < end) { --end; } //左边选大 while (arr[begin] <= arr[keyi] && begin < end) { ++begin; } //小的换到右边,大的换到左边 swap(&arr[begin], &arr[end]); } swap(&arr[keyi], &arr[end]); keyi = end; //[left,keyi-1]keyi[keyi+1,right] QuickSort(arr, left, keyi - 1); QuickSort(arr,keyi + 1,right); }
时间复杂度: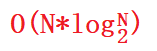
快速排序的过程类似于二叉树其高度为logN,每层约有N个数,如下图所示: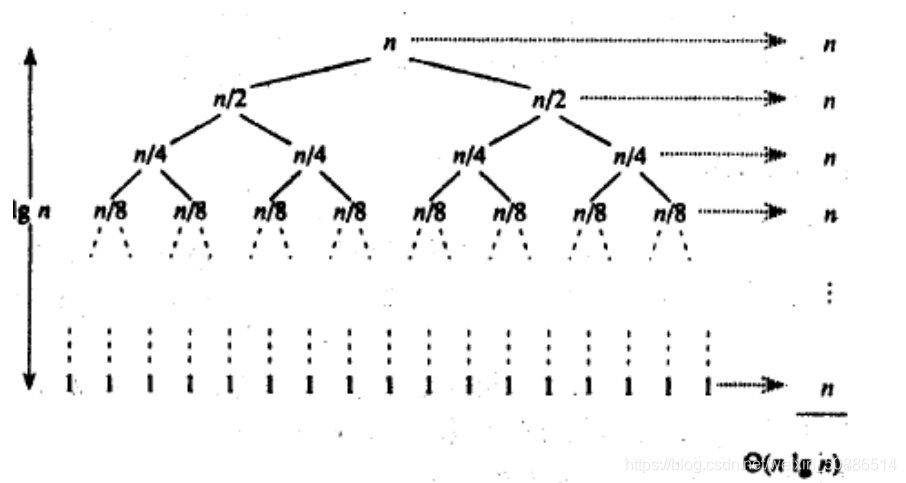
6.2 挖坑法
思路:
挖坑法思路与hoare版本(左右指针法)思路类似
1.选出一个数据(一般是最左边或是最右边的)存放在key变量中,在该数据位置形成一个坑
2、还是定义一个L和一个R,L从左向右走,R从右向左走。(若在最左边挖坑,则需要R先走;若在最右边挖坑,则需要L先走)
后面的思路与hoare版本(左右指针法)思路类似在此处就不说了
代码如下:
//快速排序法 挖坑法 void QuickSort1(int* arr, int begin, int end) { if (begin >= end) return; int left = begin,right = end; int key = arr[begin]; while (begin < end) { //找小 while (arr[end] >= key && begin < end) { --end; } //小的放到左边的坑里 arr[begin] = arr[end]; //找大 while (arr[begin] <= key && begin < end) { ++begin; } //大的放到右边的坑里 arr[end] = arr[begin]; } arr[begin] = key; int keyi = begin; //[left,keyi-1]keyi[keyi+1,right] QuickSort1(arr, left, keyi - 1); QuickSort1(arr, keyi + 1, right); }
5.3 前后指针法
思路:
1、选出一个key,一般是最左边或是最右边的。
2、起始时,prev指针指向序列开头,cur指针指向prev+1。
3、若cur指向的内容小于key,则prev先向后移动一位,然后交换prev和cur指针指向的内容,然后cur指针++;若cur指向的内容大于key,则cur指针直接++。如此进行下去,直到cur到达end位置,此时将key和++prev指针指向的内容交换即可。
经过一次单趟排序,最终也能使得key左边的数据全部都小于key,key右边的数据全部都大于key。
然后也还是将key的左序列和右序列再次进行这种单趟排序,如此反复操作下去,直到左右序列只有一个数据,或是左右序列不存在时,便停止操作
代码如下:
//快速排序法 前后指针版本 void QuickSort2(int* arr, int begin, int end) { if (begin >= end) return; int cur = begin, prev = begin - 1; int keyi = end; while (cur != keyi) { if (arr[cur] < arr[keyi] && ++prev != cur) { swap(&arr[cur], &arr[prev]); } ++cur; } swap(&arr[++prev],&arr[keyi]); keyi = prev; //[begin,keyi -1]keyi[keyi+1,end] QuickSort2(arr, begin, keyi - 1); QuickSort2(arr, keyi + 1, end); }
原文来自于:https://blog.csdn.net/weixin_50886514/article/details/119045154?utm_source=app&app_version=4.5.8