读书笔记：
关键词：论证数学，求方问题，新月形面积定理，代数数与超越数，化圆为方。
字数：4286
开篇：论证数学的建立
据考古记载，古埃及人在公元2000年以前，便建立了原始数系，并具备了某些有关三角形的和棱锥体等的几何概念。例如，古埃及建筑师用一种非常巧妙的方法确定直角，它们把12段等长的绳子相互连成环状（3,4,5），于是就形成了直角三角形。他们将这种构形放在地上，让工人们按照这个构形在金字塔、庙宇或其他建筑的拐角处建立成标准的直角。现在看来，古埃及人无疑利用了勾股定理的逆定理，然而遗憾的是没有任何资料表明，古埃及人是如何证明这种关系的，也许他们掌握某种逻辑论证，以支持它们对3-4-5三角形的观察；也许他们仅仅是靠反复实验。但无论如何，在埃及的文字记载中都没有发现通过严密的逻辑推理，证明一般数学规律的迹象。然而这种知其然而不知其所以然的结论，极可能是危险的。直到公元前1000年，论证数学（一种重点放在证明判定关系上的理论演绎体系）的出现打破了数学上的这种危险的格局。论证数学是由古代圣贤之一的泰勒斯提出的。他是第一个在"知其然"的同时提出"知其所以然"的学者，被公认为论证数学之父。因此，泰勒斯是最早的著名数学家。他是将纯粹基于实践的哲学上升到理论高度的第一人。
泰勒斯曾极力主张，对几何陈述，不能仅凭直觉上的貌似合理就予以接受。相反，必须要经过严密的逻辑证明。这是他留给数学界的一笔相当可观的遗产。
传统上认为，泰勒斯第一个证明了下列几何性质：
一、对顶角相等。
二、三角形的内角和等于两个直角之和。
三、等腰三角形的两个底角相等。
四、半圆上的圆周角是直角。
这里先不讨论其证明问题，先看一下古希腊人的数学之美。
探讨求方问题
古希腊人被几何的对称性，视觉美和微妙的逻辑结构所深深的吸引，其以简单和初步的东西作为复杂和纷繁问题基础的方式在将要探讨的欧几里得定理时，就会显得淋漓尽致。由于技术水平所限，当时的古希腊人在几何作图上仅仅依赖两种非常简单的工具，直尺（没有刻度的）和圆规。聪敏的几何家利用这两种简单的工具，便可绘制出丰富多彩和各式各样的几何图形，从平分线段和角，绘制平行线和垂直线，到创造优美的正多边形，不一而足。然而更加严重的挑战却是平面图形的求方问题。
一个平面图形的求方问题就是只用圆规和直尺作出面积等于原平面图形的正方形。如果一个平面图形的求面积能实现，我们就说这个图形是可用等价平方表示的（或者说可为平方的）。
求面积问题能够引起希腊人的兴趣并不奇怪。从纯粹实践的观点看，确定一个不规则图形的面积当然不是一件易事。但如果这个不规则图形能够用一个等面积的正方形替换，那么，确定原不规则图形面积的问题就变成了确定正方形面积的简单问题。
毫无疑问，希腊人对求面积问题的强烈爱好已经超出了实践范围。因为如果求方能够实现，就用规则的对称性正方形替换了不规则不对称的平面图形。对于那些寻求以理性和秩序支配自然世界的人来说，这在很大程度上是一个由不对称到对称，变缺陷为完美，以有理取代无理性的过程。在这种意义上，求面积问题就不仅是人类理性的象征，而且也是宇宙本身所固有的和谐和美的象征。
对于希腊数学家来说，探讨求面积问题是一个特别具有吸引力的课题，为此，他们作出了许多巧妙的几何图形。解数学问题，答案常常是一步一步推导出来的，求面积也是如此，第一步先要求出一个大体"规则"的图形的面积，然后再以此为基础，继续推导出更不规则，更稀奇古怪图形的面积。在这一过程中，关键性的第一步是要求出长方形的面积。
第一步 求长方形面积。
作任意长方形BCDE。必须只用圆规和直尺作出与BCDE面积相等的正方形。
做法：
用直尺将线段BE向右延长，再用圆规在延长线上截取长度等于ED的线段EF，使
，然后，等分BF与G（用圆规和直尺的一种简单作图），然后以G为圆心，以 
为半径作半圆。最后，过E点作线段EH垂直于BF，这里， H是垂线与半圆的交点，据此，做出正方形EKLH。如下图所示：
据此可以说，我们刚刚做出的图形——边长为的正方形EKLH与原长方形BCDE面积相等。证明：
设a、b、c分别等于线段HG、EG、EH的长度。由于所作△GEH是直角三角形，根据勾股定理，a^2 = b^2 + c^2，或等价移项，a^2 - b^2 = c^2。易知S（BCDE） = （a+b）（a-b） = c^2，又因为我们作的正方形EKLH的面积也为c^2，这样，我们就证明了原长方形面积等于我们用圆规和直尺所作正方形的面积，并以此完成了长方形的求方。求出长方形的面积后，很快便可进入下一步，求更加不规则图形的面积。
第二步 求三角形面积。
如图，已知△BCD，经D点作BC的垂线，与BC相交于E。已知三角形面积等于1/2（底）×（高） = 1/2
。如果我们平分DE与F，并作长方形，使
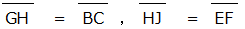。易知所作长方形的面积等于△BCD的面积（注:逻辑严密的证明即用到初中所学的割补法）。然后，我们按照第一步的步骤，作正方形，并使之面积等于该长方形的面积，因而，该正方形的面积也等于△BCD的面积。至此，三角形的求方完成。
下面，我们将讨论一个非常一般的图形。
第三步 求多边形的面积。
首先，考虑一个非常一般的多边形，如上图。我们可以通过作对角线，将这个多边形划分为三个三角形，即B、C和D。因此，整个多边形的面积就等于B+C+D。由于，我们已经知道三角形是可用等价平方表示的，因此，我们可以分别以边长b、c和d作正方形，并得到面积B、C和D。如下图：
然后，以b和c为直角边，作直角三角形，其斜边长为x，即x^2 = b^2 + c^2，我们再以x和d作为直角边，作直角三角形，其斜边为y，因而y^2 = x^2 + d^2。最后，我们便可以以y为边长作正方形。如下图：
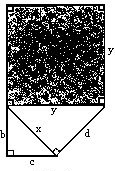
综合上述推论，就得到y^2 = x^2 + d^2 = （b^2 + c^2）+ d^2 = B + C + D，因此，原多边形的面积就等于以y为边长的正方形的面积。
显然，这一推导过程适用于任何可作对角线将其划分为四个、五个或任何数量三角形的多边形。于是问题一下子拓展出去，不论什么样的多边形，我们都可以将其划分为若干三角形，并按照第2步的方法，作每个三角形的等面积正方形，然后，根据勾股定理，利用每一个正方形，做出大正方形，其面积即等于原多边形的面积。总而言之，多边形是可用等价平方表示的。类似的，如果一个图形的面积为两个可用等价平方表示的面积之差，我们也可以将其化为正方形。
希波克拉底时代的希腊人利用上述方法可以将杂乱无章的不规则多边形变为等面积正方形。但是，这一成就却因一个明显的事实而减色不少，即这些图形都是直线图形——他们的边虽然数量众多，并构成各种奇形怪状的角度，但都只是直线。而更为严重的挑战是，曲边图形（即所谓曲线图形）是否也可以用等价平方表示。起初，人们认为，这似乎是不可能的，因为显然没有办法用圆规和直尺将曲线拉直。因此，当希俄斯的希波克拉底与公元前5世纪成功地将一种称为"新月形"（一种边缘为两个圆弧的平面图形——即月牙形）的曲线化为正方形时，世人惊得目瞪口呆。
伟大的定理：求新月形面积
希波克拉底的论证是建立在三个初步公理之上的：
- 勾股定理
- 半圆上的圆周角是直角
- 两个圆形或半圆形的面积之比等于其直径的平方比。
希波克拉底的证明方法简单又高明。即他必须首先证实所论证的新月形面积等于下图阴影部分△AOC，然后再利用三角形求方公理来断定新月形求方同样可以实现。这一经典论证的详细过程如下：
定理：新月形AECF可用等价平方表示。
证明：如下图，首先以O为圆心，以 
为半径作半圆。作OC垂直于AB，且与半圆相交于C，并连接AC与BC。平分AC与D，然后，以D为圆心，以AD为半径作半圆AEC，这样就形成了如图中阴影所示的新月形AECF。
根据"边角边"全等定理，三角形AOC和BOC全等，所以有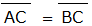
。又因为∠ACB内接于半圆，所以∠ACB是直角。然后我们应用勾股定理
。因为AB是半圆ACB的直径，AC是半圆AEC的直径，所以可以应用上述第三条原理，即得到
也就是说，半圆AEC的面积是半圆ACB的面积的一半，据此我们可以直接得出：面积(半圆AEC) = 面积(扇形AECO)，最后，我们只需从这两个图形中各自减去它们共同的部分AFCD，即可得到：面积(新月形AECF) = 面积(△ACO)。我们已知，我们可以做一个正方形，使其面积等于三角形ACO，因此也等于新月形AECF的面积。这就是我们所寻求的化新月形为方的问题。证迄。
对于这一数学史上的一大成就。评注家普罗克洛斯（公元410-485）以他五世纪的眼光，认为希俄斯的希波克拉底"...作出了新月形的等面积正方形，并在几何学中做出过许多其他发现，是一位作图的天才，如果曾经有过这种天才的话。"
后记：
由于希波克拉底求新月形面积的成功，希腊数学家对求完美的曲线图形—圆的面积充满了乐观。但是情况却并非如此。一代又一代的人经过数百年的努力，始终未能化圆为方。历经种种曲折。人们提出了无数的解法，但最后发现，每一种解法都有错误。逐渐的，数学家们开始怀疑，也许根本不可能用圆规和直尺做出圆的等面积正方形。当然，缺乏一种正确的证明方法，即使经过了2000年的努力，也依然不表明化圆为方是不可能的；也许，数学家只是不够聪明，还没有找到一条穿越几何丛林的道路。此外，如果化圆为方不可能的话，就必须借助其他逻辑严密的定理来证明这一事实，而人们也不清楚如何做出类似证明。
应当指出一点，没有人会怀疑，已知一个圆，必然存在着一个与之面积相等的正方形。例如，已知一个固定的圆和圆旁的一个正方形投影小光点，并且正方形投影的面积大大小于圆的面积。如果我们连续移动投影仪，使之距离投影屏面越来越远，并以此逐渐扩大正方形投影的面积，这样，我们最终会得到一个面积超过圆面积的正方形，根据"逐渐扩大"的直观概念，我们可以得出正确结论，在过程的某一瞬间，正方形的面积恰好等于圆形面积。
但是，这毕竟有点离题。不要忘记问题的关键不是是否存在这样一个正方形（实际上是存在的，如果抛开只用尺规的限制，就可以解决，如西皮阿斯的割圆曲线，阿基米德大牛的螺线等），而是是否可以用圆规和直尺作出这个正方形。这就出现了困难，因为几何学家只限于使用这两种特定工具；而移动投影光点显然违反这一规则。
从希波克拉底时代直到1882年，作为古希腊三大几何难题之一的化圆为方问题（另外两个是三等分角问题和倍立方问题）在经过了人们2000年的之久的努力探索之后，终于被德国数学家费迪南德•林德曼成功而明确地证明了化圆为方是不可能的。其核心技术细节就是林德曼证明了π是超越数（对于这种大师级的专业问题的证明，其技术细节相当高深，这里就不越俎代庖了，感兴趣的可以用你手中的利器——搜索引擎）。而实数包括了两个互斥的两个类型代数数（可构造数是代数数的真子集）和超越数。如下图。
而问题是对于给定的单位长度"1"，用尺规作图法只能作出很"小"一部分代数数，肯定作不出超越数，而林德曼恰恰证明了π是超越数。而化圆为方相当于用尺规作出π值。为什么这么说呢？一个单位圆面积是π，若能作出一个长度为π的线段，以这个线段作边，单位线段为另一边作矩形，显然这个矩形的面积和单位圆的面积相等。然后利用矩形求方公理我们就实现了"化圆为方"了。因此，长度π就应该能用尺规构造，而如林德曼所述，π是超越数，不可构造的，即用尺规作图法是不可能做出π值的。利用上述反证法，我们可以得出结论化圆为方在逻辑上是根本不可能的。
应当注意的一点是有些人认为化圆为方的全部困难在于π值不可能用有尽的小数表示出来，这种看法似是而非。比如，没有比做出它更容易的了。究起本源，尺规作图无法实现化圆为方的本质，原因在于几何尺规作图中的圆规自身不存在度量弧的功能。
林德曼的发现表明，从希波克拉底时代直到现代数学家对化圆为方这一难题的可以探索，实际上是徒劳的。从化新月形为方开始，所有有启发性的证明，所有有希望的线索，到头来都成了虚幻镜影。然而，这并不意味着人们两千多个冬夏夜以继日研究的汗水就白流了。在这个过程中又有一些重要的思想开始萌芽，比如含有原始积分思想的穷竭法，阿基米德螺线，割圆曲线求直曲线法等等对后来数学研究的发展都起到了不可小觑的作用。再者，这种探索本身就是人类的价值所在和需要，没有这类探索，人类不可能获知大自然的奥秘（或许还浸淫在齐天大圣无所不能的幻梦中呢）；没有这类探索，最终仍不知道西红柿不但好看而且好吃，螃蟹不好看但是好吃，蜘蛛不好看也不好吃。为实用目的而探索，值得提倡；为求知而探索，也应鼓励。后者正是科学精神的精髓，也是人类价值的体现之一。人类不但能用智慧解决生存的物质问题，而且可能并且应该解决生活的精神食粮问题——"数学也是一种文化"。不记得谁曾说过：世界上真正迷人的科学只有两种——数学与哲学。同样也不记得是谁说过，任何学科的发展如果都能上升到数学的高度解决问题才算是完善的（大体意思是这样的:）。
希波克拉底及其新月形的故事便就此划上了句号，而且，这是一个相当曲折反复的故事。起初，直觉认为，不可能用尺规作出曲线图形的等价正方形。但是，希波克拉底通过新月形求方将直觉颠倒过来，并继续寻求更多可用等价平方表示的曲线图形。然而，最后，林德曼、切巴托鲁和多罗德诺的否定结论表明，直觉并非一无是出。曲线图形的求方远非规范，而必定永远只是例外（直到20世纪，切巴托鲁和多罗德诺才证明出了只有五种新月形是唯一可用等价平方表示的新月形）。
参考资料：
主料：《天才引导的历程》
调料：《说不尽的π》
最后，调侃一下，熬夜有罪啊:)
All Rights Reserved.
Author：海峰:)
Copyright © xp_jiang.