题解【UVA12097】Pie

题目描述

输入格式

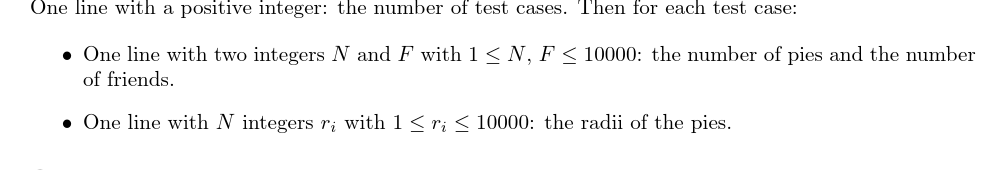
输出格式

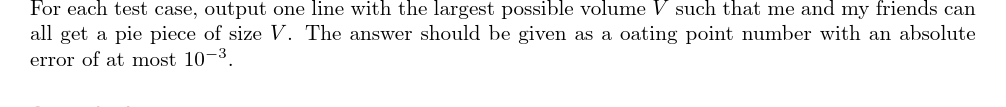
输入输出样例

输入样例#1

3
3 3
4 3 3
1 24
5
10 5
1 4 2 3 4 5 6 5 4 2

输出样例#1

25.1327
3.1416
50.2655

题意简述

题目描述

有(F+1)个人来分(N)个圆形派，每个人得到的必须是一整块派，而不是几块拼在一起。而且派的面积要相同。求每个人最多得到多大面积的派（不必是圆形）

输入格式

输入的第一行为数据组数(T)。

每组数据的第一行为两个整数(N)和(F(1<=N,F<=10000));

第二行为(N)个整数(r_i(1<=r_i<=10000)),即各个派的半径。

输出格式

对于每组数据，输出每个人得到的派的面积的最大值，精确到(10^{-3})。

题解

此题可以使用二分答案的方法，

把问题转换成“是否每个人都可以得到一块面积为(x)的派”。

这样的转换就使问题增加了一个条件。

求解的目标就变成了“这一些条件是不是矛盾”。

如果有矛盾，是怎样的矛盾呢？

只有一种矛盾：(x)太大，满足不了所有的(F+1)个人。

这样，我们就只需要计算一共可以切多少份面积为(x)的派，

然后看一看这个数目够不够(F+1)即可。

由于派不可以拼起来，

因此一个半径为(r)的派就只可以切出(lfloor frac{pi imes r^{2}}{x} floor) 个派，

其余的部分就只能浪费了。

然后把所有能切出来的份数相加即可。

代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cctype>

using namespace std;

inline int gi()
{
    int f = 1, x = 0; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar();}
    while (c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar();}
    return f * x;
}

const double pi = acos(-1.0), eps = 1e-4;
int n, m, t;//m即为题意中的F
double a[10003], ans;

inline bool check(double mian)//二分答案的判断函数
{
	int cnt = 0;
	for (int i = 0; i < n; i++) 
	{
		cnt = cnt + floor(a[i] / mian);//加上能拼成的块数
	}
	return cnt > m;//判断是否大于等于m+1
}

int main()
{
	t = gi();
	while (t--)//多组数据
	{
		n = gi(), m = gi();
		double p = -1;
		for (int i = 0; i < n; i++)
		{
			int R = gi();
			a[i] = pi * R * R, p = max(p, a[i]);//计算每份派的面积及最大派的面积
		}
		double l = 0, r = p;
		while ((r - l) > eps)//开始二分答案
		{
			double mid = (l + r) / 2;
			if (check(mid))
			{
				l = mid;
			}
			else 
			{
				r = mid;
			}
		}
		printf("%0.4lf
", l);//输出
	}
	return 0;//结束
}