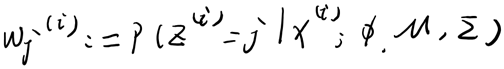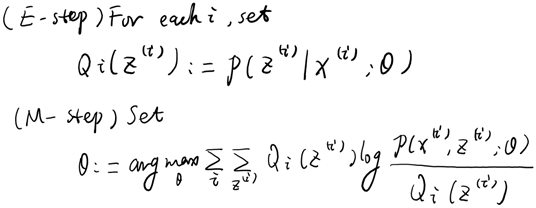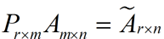1 Unsupervised Learning
1.1 k-means clustering algorithm
1.1.1 算法思想
1.1.2 k-means的不足之处
1.1.3 如何选择K值
1.1.4 Spark MLlib 实现 k-means 算法
1.2 Mixture of Gaussians and the EM algorithm
1.3 The EM Algorithm
1.4 Principal Components Analysis
1.4.1 算法原理
1.4.2 奇异值与主成分分析（PCA）
1.4.3 Spark MLlib 实现PCA
参考文献
附 录
Andrew Ng 在斯坦福大学的CS229机器学习课程内容
中英文词语对照
1. Unsupervised Learning
1.1 k-means clustering algorithm
1.1.1 算法思想
聚类其核心任务是：将一组目标object划分为若干个簇，每个簇之间的object尽可能的相似，簇与簇之间的object尽可能的相异。聚类算法是机器学习（或者说是数据挖掘更合适）中重要的一部分，除了最为简单的K-Means聚类算法外，较常见的还有：层次法（CURE、CHAMELEON等）、网格算法（STING、WaveCluster等）等等。
较权威的聚类问题定义：所谓聚类问题，就是给定一个元素集合D，其中每个元素具有n个可观察属性，使用某种算法将D划分成k个子集，要求每个子集内部的元素之间相异度尽可能低，而不同子集的元素相异度尽可能高。其中每个子集叫做一个簇。
聚类属于无监督学习，k-means 算法是聚类中最简单的一种，但其思想却不简单。监督学习比如逻辑回归、朴素贝叶斯和 SVM 等的训练数据中已经包含了类别的标签Y，而聚类的标签中只包含特征X。
图 无监督学习
在聚类问题中，给我们的训练样本是，每个。
K-means算法是将样本聚类成k个簇（cluster），具体算法描述如下：
对于每一个类j，重新计算该类的质心
} |
即，
K是我们事先给定的聚类数，代表样例i与k个类中距离最近的那个类，的值是1到k中的一个。质心代表我们对属于同一个类的样本中心点的猜测。
下图展示了对n个样本点进行K-means聚类的效果，这里k取2。
K-means面对的第一个问题是如何保证收敛，前面的算法中强调结束条件就是收敛，可以证明的是K-means完全可以保证收敛性。下面我们定性的描述一下收敛性，我们定义畸变函数（distortion function）如下：
J函数表示每个样本点到其质心的距离平方和。K-means是要将J调整到最小。假设当前J没有达到最小值，那么首先可以固定每个类的质心，调整每个样例的所属的类别来让J函数减少，同样，固定，调整每个类的质心也可以使J减小。这两个过程就是内循环中使J单调递减的过程。当J递减到最小时，和c也同时收敛。（在理论上，可以有多组不同的和c值能够使得J取得最小值，但这种现象实际上很少见）。
由于畸变函数J是非凸函数，意味着我们不能保证取得的最小值是全局最小值，也就是说k-means对质心初始位置的选取比较感冒，但一般情况下k-means达到的局部最优已经满足需求。但如果你怕陷入局部最优，那么可以选取不同的初始值跑多遍k-means，然后取其中最小的J对应的和c输出。
1.1.2 k-means的不足之处
首先对初值敏感，由于只能收敛到局部最优，初值很大程度上决定它收敛到哪里；
从算法的过程可以看出，k-means对椭球形状的簇效果最好，不能发现任意形状的簇；
对孤立点干扰的鲁棒性差，孤立点，是异质的，可以说是均值杀手，k-means又是围绕着均值展开的，原离簇的孤立点对簇的均值的拉动作用是非常大的。
针对这些问题后来又有了基于密度的DBSCAN算法，最近Science上发了另一篇基于密度的方法：Clustering by fast search and find of density peaks。基于密度的方法无论对clustering还是outliers detection效果都不错，和 k-means不同，这些算法已经没有了目标函数，但鲁棒性强，可以发现任意形状的簇。 另外如何自动确定k-means的k是目前研究较多的一个问题。
1.1.3 如何选择K值
《大数据——互联网大规模数据挖掘与分布式处理》中提到：给定一个合适的类簇指标，比如平均半径或直径，只要我们假设的类簇的数目等于或者高于真实的类簇的数目时，该指标上升会很缓慢，而一旦试图得到少于真实数目的类簇时，该指标会急剧上升。
类簇的直径是指类簇内任意两点之间的最大距离。
类簇的半径是指类簇内所有点到类簇中心距离的最大值。
下图是当K的取值从2到9时，聚类效果和类簇指标的效果图：
左图是K取值从2到7时的聚类效果，右图是K取值从2到9时的类簇指标的变化曲线，此处我选择类簇指标是K个类簇的平均质心距离的加权平均值。从上图中可以明显看到，当K取值5时，类簇指标的下降趋势最快，所以K的正确取值应该是5。
Andrew Ng 如是说：
1.1.4 Spark MLlib 实现 k-means 算法
测试数据
|
0.0 0.0 0.0 0.1 0.1 0.1 0.2 0.2 0.2 9.0 9.0 9.0 9.1 9.1 9.1 9.2 9.2 9.2 15.1 16.1 17.0 18.0 17.0 19.0 20.0 21.0 22.0 |
测试数据不用带标签，数据分为3个维度。
代码示例
Java code
|
private static final Pattern SPACE = Pattern.compile(" ");
public static void main(String[] args) { SparkConf sparkConf = new SparkConf() .setAppName("K-Means") .setMaster("local[2]"); JavaSparkContext sc = new JavaSparkContext(sparkConf); JavaRDD<String> data = sc.textFile("/home/yurnom/data/kmeans_data.txt"); JavaRDD<Vector> parsedData = data.map(s -> { double[] values = Arrays.asList(SPACE.split(s)) .stream() .mapToDouble(Double::parseDouble) .toArray(); return Vectors.dense(values); });
int numClusters = 3; //预测分为3个簇类 int numIterations = 20; //迭代20次 int runs = 10; //运行10次，选出最优解 KMeansModel clusters = KMeans.train(parsedData.rdd(), numClusters, numIterations, runs);
//计算测试数据分别属于那个簇类 print(parsedData.map(v -> v.toString() + " belong to cluster :" + clusters.predict(v)).collect()); //计算cost double wssse = clusters.computeCost(parsedData.rdd()); System.out.println("Within Set Sum of Squared Errors = " + wssse);
//打印出中心点 System.out.println("Cluster centers:"); for (Vector center : clusters.clusterCenters()) { System.out.println(" " + center); } //进行一些预测 System.out.println("Prediction of (1.1, 2.1, 3.1): " + clusters.predict(Vectors.dense(new double[]{1.1, 2.1, 3.1}))); System.out.println("Prediction of (10.1, 9.1, 11.1): " + clusters.predict(Vectors.dense(new double[]{10.1, 9.1, 11.1}))); System.out.println("Prediction of (21.1, 17.1, 16.1): " + clusters.predict(Vectors.dense(new double[]{21.1, 17.1, 16.1}))); }
public static <T> void print(Collection<T> c) { for(T t : c) { System.out.println(t.toString()); } } |
结果
|
[0.0,0.0,0.0] belong to cluster :0 [0.1,0.1,0.1] belong to cluster :0 [0.2,0.2,0.2] belong to cluster :0 [9.0,9.0,9.0] belong to cluster :1 [9.1,9.1,9.1] belong to cluster :1 [9.2,9.2,9.2] belong to cluster :1 [15.1,16.1,17.0] belong to cluster :2 [18.0,17.0,19.0] belong to cluster :2 [20.0,21.0,22.0] belong to cluster :2
Within Set Sum of Squared Errors = 38.533333333333815 Cluster centers: [0.10000000000000002,0.10000000000000002,0.10000000000000002] [9.1,9.1,9.1] [17.7,18.033333333333335,19.333333333333332] Prediction of (1.1, 2.1, 3.1): 0 Prediction of (10.1, 9.1, 11.1): 1 Prediction of (21.1, 17.1, 16.1): 2 |
1.2 Mixture of Gaussians and the EM algorithm
本节讨论使用期望最大化算法（Exception-Maximization）进行密度估计（density-estimation）。
高斯模型有单高斯模型（SGM）和混合高斯模型（GMM）两种。
单高斯模型
为简单起见，阈值t的选取一般靠经验值来设定。通常意义下，我们一般取t=0.7-0.75之间。
二维情况如下所示：
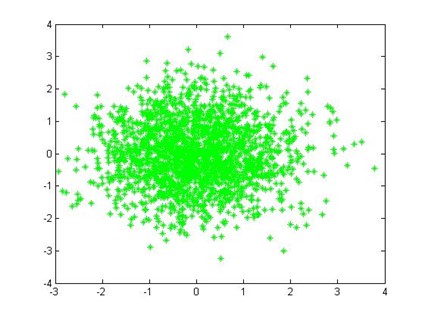
混合高斯模型
对于(b)图所示的情况，很明显，单高斯模型是无法解决的。为了解决这个问题，人们提出了高斯混合模型（GMM），顾名思义，就是数据可以看作是从数个高斯分布中生成出来的。虽然我们可以用不同的分布来随意地构造 XX Mixture Model ，但是 GMM是 最为流行。另外，Mixture Model 本身其实也是可以变得任意复杂的，通过增加 Model 的个数，我们可以任意地逼近任何连续的概率密分布。
每个 GMM 由 K 个 Gaussian 分布组成，每个 Gaussian 称为一个"Component"，这些 Component 线性加成在一起就组成了 GMM 的概率密度函数：
其中，
表示选中这个component部分的概率，我们也称其为加权系数。
根据上面的式子，如果我们要从 GMM 的分布中随机地取一个点的话，
首先随机地在这 K 个 Component 之中选一个，每个 Component 被选中的概率实际上就是它的系数 πk，选中了 Component 之后，再单独地考虑从这个 Component 的分布中选取一个点就可以了──这里已经回到了普通的 Gaussian 分布，转化为了已知的问题。假设现在有 N 个数据点，我们认为这些数据点由某个GMM模型产生，现在我们要需要确定 πk,μk,σk 这些参数。很自然的，我们想到利用最大似然估计来确定这些参数，GMM的似然函数如下：
在最大似然估计里面，我们的目的是把乘积的形式分解为求和的形式，即在等式的左右两边加上一个log函数。
具体来说，与k-means一样，给定的训练样本是，我们将隐含类别标签用表示。与k-means的硬指定不同，我们首先认为是满足一定的概率分布的，这里我们认为满足多项式分布，，其中，有k个值{1,…,k}可以选取。而且我们认为在给定后，满足多值高斯分布，即。由此可以得到联合分布。
整个模型简单描述为对于每个样例，我们先从k个类别中按多项式分布抽取一个，然后根据所对应的k个多值高斯分布中的一个生成样例，。整个过程称作混合高斯模型。注意的是这里的仍然是隐含随机变量。模型中还有三个变量和。最大似然估计为。对数化后如下：
这个式子的最大值是不能通过前面使用的求导数为0的方法解决的，因为求的结果不是close form。但是假设我们知道了每个样例的，那么上式可以简化为：
这时候我们再来对和进行求导得到：
就是样本类别中的比率。是类别为j的样本特征均值，是类别为j的样例的特征的协方差矩阵。
实际上，当知道后，最大似然估计就近似于高斯判别分析模型（Gaussian discriminant analysis model）了。所不同的是GDA中类别y是伯努利分布，而这里的z是多项式分布，还有这里的每个样例都有不同的协方差矩阵，而GDA中认为只有一个。
之前我们是假设给定了，实际上是不知道的。那么怎么办呢？考虑之前提到的EM的思想，第一步是猜测隐含类别变量z，第二步是更新其他参数，以获得最大的最大似然估计。用到这里就是：
|
循环下面步骤，直到收敛： { （E步）对于每一个i和j，计算
（M步），更新参数：
} |
在E步中，我们将其他参数看作常量，计算的后验概率，也就是估计隐含类别变量。估计好后，利用上面的公式重新计算其他参数，计算好后发现最大化最大似然估计时，值又不对了，需要重新计算，周而复始，直至收敛。
的具体计算公式如下：
这个式子利用了贝叶斯公式。
这里我们使用代替了前面的，由简单的0/1值变成了概率值。
1.3 The EM Algorithm
给定的训练样本是，样例间独立，我们想找到每个样例隐含的类别z，能使得p(x,z)最大。p(x,z)的最大似然估计如下：
第一步是对极大似然取对数，第二步是对每个样例的每个可能类别z求联合分布概率和。但是直接求一般比较困难，因为有隐藏变量z存在，但是一般确定了z后，求解就容易了。
EM是一种解决存在隐含变量优化问题的有效方法。竟然不能直接最大化，我们可以不断地建立的下界（E步），然后优化下界（M步）。这句话比较抽象，看下面的。
对于每一个样例i，让表示该样例隐含变量z的某种分布，满足的条件是。（如果z是连续性的，那么是概率密度函数，需要将求和符号换做积分符号）。如果隐藏变量连续的，那么使用高斯分布，如果隐藏变量是离散的，那么就使用伯努利分布了。
可以由前面阐述的内容得到下面的公式：
（1）到（2）比较直接，就是分子分母同乘以一个相等的函数。（2）到（3）利用了Jensen不等式，考虑到是凹函数（二阶导数小于0），而且
就是
的期望（回想期望公式中的Lazy Statistician规则）
|
设Y是随机变量X的函数（g是连续函数），那么 X是离散型随机变量，它的分布律为，k=1,2,…。若绝对收敛，则有 X是连续型随机变量，它的概率密度为，若绝对收敛，则有 |
对应于上述问题，Y是
，X是，是，g是到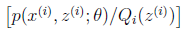
的映射。这样解释了式子（2）中的期望，再根据凹函数时的Jensen不等式：
可以得到（3）。
这个过程可以看作是对求了下界。对于的选择，有多种可能，那种更好的？假设已经给定，那么的值就决定于和了。我们可以通过调整这两个概率使下界不断上升，以逼近的真实值，那么什么时候算是调整好了呢？当不等式变成等式时，说明我们调整后的概率能够等价于了。按照这个思路，我们要找到等式成立的条件。根据Jensen不等式，要想让等式成立，需要让随机变量变成常数值，这里得到：
c为常数，不依赖于。对此式子做进一步推导，我们知道，那么也就有，（多个等式分子分母相加不变，这个认为每个样例的两个概率比值都是c），那么有下式：
至此，我们推出了在固定其他参数后，的计算公式就是后验概率，解决了如何选择的问题。这一步就是E步，建立的下界。接下来的M步，就是在给定后，调整，去极大化的下界（在固定后，下界还可以调整的更大）。那么一般的EM算法的步骤如下：
|
循环重复直到收敛 {
|
那么究竟怎么确保EM收敛？假定和是EM第t次和t+1次迭代后的结果。如果我们证明了，也就是说极大似然估计单调增加，那么最终我们会到达最大似然估计的最大值。下面来证明，选定后，我们得到E步
这一步保证了在给定时，Jensen不等式中的等式成立，也就是
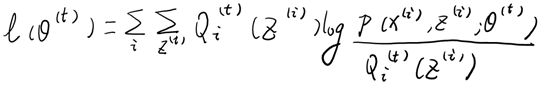
然后进行M步，固定，并将视作变量，对上面的求导后，得到，这样经过一些推导会有以下式子成立：
解释第（4）步，得到时，只是最大化，也就是的下界，而没有使等式成立，等式成立只有是在固定，并按E步得到时才能成立。
况且根据我们前面得到的下式，对于所有的和都成立
第（5）步利用了M步的定义，M步就是将调整到，使得下界最大化。因此（5）成立，（6）是之前的等式结果。
这样就证明了会单调增加。一种收敛方法是不再变化，还有一种就是变化幅度很小。
再次解释一下（4）、（5）、（6）。首先（4）对所有的参数都满足，而其等式成立条件只是在固定，并调整好Q时成立，而第（4）步只是固定Q，调整，不能保证等式一定成立。（4）到（5）就是M步的定义，（5）到（6）是前面E步所保证等式成立条件。也就是说E步会将下界拉到与一个特定值（这里）一样的高度，而此时发现下界仍然可以上升，因此经过M步后，下界又被拉升，但达不到与另外一个特定值一样的高度，之后E步又将下界拉到与这个特定值一样的高度，重复下去，直到最大值。
如果我们定义
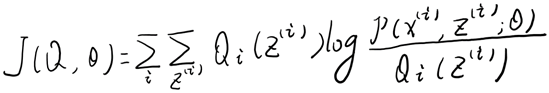
从前面的推导中我们知道，EM可以看作是J的坐标上升法，E步固定，优化，M步固定优化。
1.4.1 算法原理
主成分分析（Principal Components Analysis -- PCA）与线性判别分析（Linear Discriminant Analysis -- LDA）有着非常近似的意思，LDA的输入数据是带标签的，而PCA的输入数据是不带标签的，所以PCA是一种unsupervised learning。LDA通常来说是作为一个独立的算法存在，给定了训练数据后，将会得到一系列的判别函数（discriminate function），之后对于新的输入，就可以进行预测了。而PCA更像是一个预处理的方法，它可以将原本的数据降低维度，而使得降低了维度的数据之间的方差最大（也可以说投影误差最小）。
PCA的计算过程：
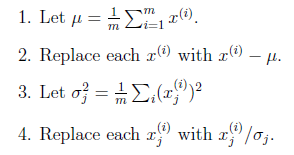
其中是样例，共m个，每个样例n个特征，也就是说是n维向量。是第i个样例的第j个特征。是样例均值。是第j个特征的标准差。
整个PCA过程貌似及其简单，就是求协方差的特征值和特征向量，然后做数据转换。但是有没有觉得很神奇，为什么求协方差的特征向量就是最理想的k维向量？其背后隐藏的意义是什么？整个PCA的意义是什么？
推导公式可以帮助我们理解。我下面将用两种思路来推导出一个同样的表达式。首先是最大化投影后的方差，其次是最小化投影后的损失（投影产生的损失最小）。
1) 最大方差法
在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。如前面的图，样本在横轴上的投影方差较大，在纵轴上的投影方差较小，那么认为纵轴上的投影是由噪声引起的。
因此我们认为，最好的k维特征是将n维样本点转换为k维后，每一维上的样本方差都很大。
比如下图有5个样本点：（已经做过预处理，均值为0，特征方差归一）
下面将样本投影到某一维上，这里用一条过原点的直线表示（前处理的过程实质是将原点移到样本点的中心点）。
假设我们选择两条不同的直线做投影，那么左右两条中哪个好呢？根据我们之前的方差最大化理论，左边的好，因为投影后的样本点之间方差最大。
这里先解释一下投影的概念：
红色点表示样例，蓝色点表示在u上的投影，u是直线的斜率也是直线的方向向量，而且是单位向量。蓝色点是在u上的投影点，离原点的距离是（即或者）由于这些样本点（样例）的每一维特征均值都为0，因此投影到u上的样本点（只有一个到原点的距离值）的均值仍然是0。
回到上面左右图中的左图，我们要求的是最佳的u，使得投影后的样本点方差最大。
由于投影后均值为0，因此方差为：
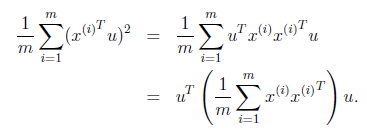
中间那部分很熟悉啊，不就是样本特征的协方差矩阵么（的均值为0，一般协方差矩阵都除以m-1，这里用m）。
用来表示，表示，那么上式写作
由于u是单位向量，即，上式两边都左乘u得，
即
就是的特征值，u是特征向量。最佳的投影直线是特征值最大时对应的特征向量，其次是第二大对应的特征向量，依次类推。
因此，我们只需要对协方差矩阵进行特征值分解，得到的前k大特征值对应的特征向量就是最佳的k维新特征，而且这k维新特征是正交的。得到前k个u以后，样例通过以下变换可以得到新的样本。
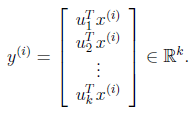
其中的第j维就是在上的投影。
通过选取最大的k个u，使得方差较小的特征（如噪声）被丢弃。
2) 最小平方误差理论
假设有这样的二维样本点（红色点），回顾我们前面探讨的是求一条直线，使得样本点投影到直线上的点的方差最大。本质是求直线，那么度量直线求的好不好，不仅仅只有方差最大化的方法。再回想我们最开始学习的线性回归等，目的也是求一个线性函数使得直线能够最佳拟合样本点，那么我们能不能认为最佳的直线就是回归后的直线呢？回归时我们的最小二乘法度量的是样本点到直线的坐标轴距离。比如这个问题中，特征是x，类标签是y。回归时最小二乘法度量的是距离d。如果使用回归方法来度量最佳直线，那么就是直接在原始样本上做回归了，跟特征选择就没什么关系了。
因此，我们打算选用另外一种评价直线好坏的方法，使用点到直线的距离d'来度量。
现在有n个样本点，每个样本点为m维（这节内容中使用的符号与上面的不太一致，需要重新理解符号的意义）。将样本点在直线上的投影记为，那么我们就是要最小化
这个公式称作最小平方误差（Least Squared Error）。
而确定一条直线，一般只需要确定一个点，并且确定方向即可。
第一步确定点：
假设要在空间中找一点来代表这n个样本点，"代表"这个词不是量化的，因此要量化的话，我们就是要找一个m维的点，使得
最小。其中是平方错误评价函数（squared-error criterion function），假设m为n个样本点的均值：
那么平方错误可以写作：
后项与无关，看做常量，而，因此最小化时，
是样本点均值。
第一步确定方向：
我们从拉出要求的直线（这条直线要过点m），假设直线的方向是单位向量e。那么直线上任意一点，比如就可以用点m和e来表示
其中是到点m的距离。
我们重新定义最小平方误差：
这里的k只是相当于i。就是最小平方误差函数，其中的未知参数是和e。
实际上是求的最小值。首先将上式展开：
我们首先固定e，将其看做是常量，，然后对进行求导，得
这个结果意思是说，如果知道了e，那么将与e做内积，就可以知道了在e上的投影离m的长度距离，不过这个结果不用求都知道。
然后是固定，对e求偏导数，我们先将公式（8）代入，得
其中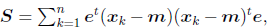
与协方差矩阵类似，只是缺少个分母n-1，我们称之为散列矩阵（scatter matrix）。
然后可以对e求偏导数，但是e需要首先满足，引入拉格朗日乘子，来使最大（最小），令
求偏导
这里存在对向量求导数的技巧，方法这里不多做介绍。可以去看一些关于矩阵微积分的资料，这里求导时可以将看作是，将看做是。
导数等于0时，得
两边除以n-1就变成了，对协方差矩阵求特征值向量了。
从不同的思路出发，最后得到同一个结果，对协方差矩阵求特征向量，求得后特征向量上就成为了新的坐标，如下图：
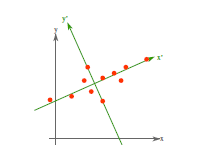
这时候点都聚集在新的坐标轴周围，因为我们使用的最小平方误差的意义就在此。
1.4.2 奇异值与主成分分析（PCA）
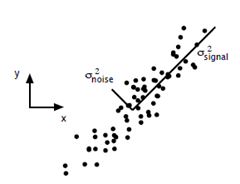
这里主要谈谈如何用SVD去解PCA的问题。PCA的问题其实是一个基的变换，使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量，我们在讲一个东西的稳定性的时候，往往说要减小方差，如果一个模型的方差很大，那就说明模型不稳定了。但是对于我们用于机器学习的数据（主要是训练数据），方差大才有意义，不然输入的数据都是同一个点，那方差就为0了，这样输入的多个数据就等同于一个数据了。以下面这张图为例子：
这个假设是一个摄像机采集一个物体运动得到的图片，上面的点表示物体运动的位置，假如我们想要用一条直线去拟合这些点，那我们会选择什么方向的线呢？当然是图上标有signal的那条线。如果我们把这些点单纯的投影到x轴或者y轴上，最后在x轴与y轴上得到的方差是相似的（因为这些点的趋势是在45度左右的方向，所以投影到x轴或者y轴上都是类似的），如果我们使用原来的xy坐标系去看这些点，容易看不出来这些点真正的方向是什么。但是如果我们进行坐标系的变化，横轴变成了signal的方向，纵轴变成了noise的方向，则就很容易发现什么方向的方差大，什么方向的方差小了。
一般来说，方差大的方向是信号的方向，方差小的方向是噪声的方向，我们在数据挖掘中或者数字信号处理中，往往要提高信号与噪声的比例，也就是信噪比。对上图来说，如果我们只保留signal方向的数据，也可以对原数据进行不错的近似了。
PCA的全部工作简单点说，就是对原始的空间中顺序地找一组相互正交的坐标轴，第一个轴是使得方差最大的，第二个轴是在与第一个轴正交的平面中使得方差最大的，第三个轴是在与第1、2个轴正交的平面中方差最大的，这样假设在N维空间中，我们可以找到N个这样的坐标轴，我们取前r个去近似这个空间，这样就从一个N维的空间压缩到r维的空间了，但是我们选择的r个坐标轴能够使得空间的压缩使得数据的损失最小。
还是假设我们矩阵每一行表示一个样本，每一列表示一个feature，用矩阵的语言来表示，将一个m * n的矩阵A的进行坐标轴的变化，P就是一个变换的矩阵从一个N维的空间变换到另一个N维的空间，在空间中就会进行一些类似于旋转、拉伸的变化。
而将一个m * n的矩阵A变换成一个m * r的矩阵，这样就会使得本来有n个feature的，变成了有r个feature了（r < n)，这r个其实就是对n个feature的一种提炼，我们就把这个称为feature的压缩。用数学语言表示就是：
但是这个怎么和SVD扯上关系呢？之前谈到，SVD得出的奇异向量也是从奇异值由大到小排列的，按PCA的观点来看，就是方差最大的坐标轴就是第一个奇异向量，方差次大的坐标轴就是第二个奇异向量…我们回忆一下之前得到的SVD式子：
在矩阵的两边同时乘上一个矩阵V，由于V是一个正交的矩阵，所以V转置乘以V得到单位阵I，所以可以化成后面的式子
将后面的式子与A * P那个m * n的矩阵变换为m * r的矩阵的式子对照看看，在这里，其实V就是P，也就是一个变化的向量。这里是将一个m * n 的矩阵压缩到一个m * r的矩阵，也就是对列进行压缩，如果我们想对行进行压缩（在PCA的观点下，对行进行压缩可以理解为，将一些相似的sample合并在一起，或者将一些没有太大价值的sample去掉）怎么办呢？同样我们写出一个通用的行压缩例子：
这样就从一个m行的矩阵压缩到一个r行的矩阵了，对SVD来说也是一样的，我们对SVD分解的式子两边乘以U的转置
这样我们就得到了对行进行压缩的式子。可以看出，其实PCA几乎可以说是对SVD的一个包装，如果我们实现了SVD，那也就实现了PCA了。
1.4.3 Spark MLlib 实现PCA
Scala code
import org.apache.spark.mllib.linalg.Vector
import org.apache.spark.mllib.linalg.Matrix
import org.apache.spark.mllib.linalg.distributed.RowMatrix
val rows: RDD[Vector] = ... // an RDD of local vectors
// Create a RowMatrix from an RDD[Vector].
val mat: RowMatrix = new RowMatrix(rows)
// Get its size.
val m = mat.numRows()
val n = mat.numCols()
// Compute the top 10 principal components.
val pc: Matrix = mat.computePrincipalComponents(10) // Principal components are stored in a local dense matrix.
// Project the rows to the linear space spanned by the top 10 principal components.
val projected: RowMatrix = mat.multiply(pc)
参考文献
[1] Machine Learning Open Class by Andrew Ng in Stanford http://openclassroom.stanford.edu/MainFolder/CoursePage.php?course=MachineLearning
[2] Yu Zheng, Licia Capra, Ouri Wolfson, Hai Yang. Urban Computing: concepts, methodologies, and applications. ACM Transaction on Intelligent Systems and Technology. 5(3), 2014
[3] Jerry Lead http://www.cnblogs.com/jerrylead/
[3]《大数据-互联网大规模数据挖掘与分布式处理》 Anand Rajaraman，Jeffrey David Ullman著，王斌译
[4] UFLDL Tutorial http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial
[5] Spark MLlib之朴素贝叶斯分类算法 http://selfup.cn/683.html
[6] MLlib - Dimensionality Reduction http://spark.apache.org/docs/latest/mllib-dimensionality-reduction.html
[7] 机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用 http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html
[8] 浅谈 mllib 中线性回归的算法实现 http://www.cnblogs.com/hseagle/p/3664933.html
[9] 最大似然估计 http://zh.wikipedia.org/zh-cn/%E6%9C%80%E5%A4%A7%E4%BC%BC%E7%84%B6%E4%BC%B0%E8%AE%A1
[10] Deep Learning Tutorial http://deeplearning.net/tutorial/
附 录
Andrew Ng 在斯坦福大学的CS229机器学习课程内容
Andrew Ng -- Stanford University CS 229 Machine Learning
This course provides a broad introduction to machine learning and statistical pattern recognition.
Topics include:
supervised learning (generative/discriminative learning, parametric/non-parametric learning, neural networks, support vector machines);
learning theory (bias/variance tradeoffs; VC theory; large margins);
unsupervised learning (clustering, dimensionality reduction, kernel methods);
reinforcement learning and adaptive control. The course will also discuss recent applications of machine learning, such as to robotic control, data mining, autonomous navigation, bioinformatics, speech recognition, and text and web data processing.
中英文词语对照
neural networks 神经网络
activation function 激活函数
hyperbolic tangent 双曲正切函数
bias units 偏置项
activation 激活值
forward propagation 前向传播
feedforward neural network 前馈神经网络(参照Mitchell的《机器学习》的翻译)
Softmax回归 Softmax Regression
有监督学习 supervised learning
无监督学习 unsupervised learning
深度学习 deep learning
logistic回归 logistic regression
截距项 intercept term
二元分类 binary classification
类型标记 class labels
估值函数/估计值 hypothesis
代价函数 cost function
多元分类 multi-class classification
权重衰减 weight decay
深度网络 Deep Networks
深度神经网络 deep neural networks
非线性变换 non-linear transformation
激活函数 activation function
简洁地表达 represent compactly
"部分-整体"的分解 part-whole decompositions
目标的部件 parts of objects
高度非凸的优化问题 highly non-convex optimization problem
共轭梯度 conjugate gradient
梯度的弥散 diffusion of gradients
逐层贪婪训练方法 Greedy layer-wise training
自动编码器 autoencoder
微调 fine-tuned
自学习方法 self-taught learning
@雪松Cedro
Microsoft MVP, Windows Platform Development