递归-汉诺塔问题

汉诺塔传说：汉诺塔问题，是源于印度一个古老的益智玩具；大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

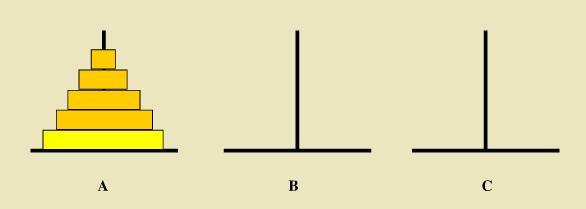
数学抽象：如下图所示，从左到右有A、B、C三根柱子，其中A柱子上面有从小叠到大的n个圆盘，现要求将A柱子上的圆盘移到C柱子上去，期间只有一个原则：一次只能移到一个盘子且大盘子不能在小盘子上面，求移动的步骤和移动的次数；

递归问题：递归是函数调用函数自身；如果一个大型复杂的问题能蹭蹭转化为一个与原问题相似的规模较小的问题，那么就能用递归来进行求解；一般来说递归需要有边界条件、递归前进端（子问题）和递归返回段（递归出口）；当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

递归函数设计技巧：

• 递归主题；
• 递归函数参数；
• 递归函数出口；
• 递归问题分析顺序：从大问题分析小问题，每次利用减治思想减少规模；

递归算法解决问题的种类：

• 数据的定义是按照递归定义的；（Fibonacci 函数）
• 问题的解法是按照递归算法进行实现；（汉诺塔问题）
• 数据的结构的形式是按照递归定义的；（二叉树，图问题，线性表：DFS搜索，归并排序，快速排序等）

汉诺塔问题递归分析：

假设一共有n个圆盘，则汉诺塔问题，以递归角度进行分析为：

• 把n-1个盘子由A移动到B；(借助辅助塔C)
• 把第n个盘子，由A移动到C;
• 把n-1个盘子由B移动到C; (借助辅助塔A) 

游戏解法：游戏要求从A->C移动；手动操作时：首先确定层数n, 如果层数是奇数，最上层由A->C; 如果层数为偶数，最上层A->B;

程序解法：

#include <iostream>
using namespace std;
int m = 0; // 移动次数

void move(int disk, char from, char to){
    cout << "移动次数:" << (++m) <<" 把块:" << disk << " 按照如下移动：" <<  from << " --> " << to << endl;
}

// 递归求解汉诺塔
void hanoi(int disks, char from, char to, char assist){
    if (disks == 1) // 递归出口；
    {
        move(disks, from, to); 
        return; 
    }
    //递归子问题；
    hanoi(disks-1, from, assist, to); // n-1个盘子，由A移动到B, 借助辅助塔C；
    move(disks, from, to); // 把第n个盘子，由A移动到C；
    hanoi(disks-1, assist, to, from); // 把n-1个盘子，由B移动到C, 借助辅助塔A；
}

int main(){
    cout << "汉诺塔问题：" << endl;
    int n = 3;
    cout << "汉诺塔圆盘个数：" << n << endl;
    // 创建三个塔；
    char A = 'A';
    char B = 'B';
    char C = 'C';
    // 递归求解汉诺塔，输出移动步骤；
    // n 个盘 从 A 塔移动到 C塔， 借助辅助塔B；
    hanoi(n, A, C, B); // 汉诺塔递归求解；
    return 0;
}

bash-3.2$ c++ 汉诺塔问题.cc; ./a.out
汉诺塔问题：
汉诺塔圆盘个数：1
移动次数:1 把块:1 按照如下移动：A --> C
bash-3.2$ c++ 汉诺塔问题.cc; ./a.out
汉诺塔问题：
汉诺塔圆盘个数：2
移动次数:1 把块:1 按照如下移动：A --> B
移动次数:2 把块:2 按照如下移动：A --> C
移动次数:3 把块:1 按照如下移动：B --> C
bash-3.2$ c++ 汉诺塔问题.cc; ./a.out
汉诺塔问题：
汉诺塔圆盘个数：3
移动次数:1 把块:1 按照如下移动：A --> C
移动次数:2 把块:2 按照如下移动：A --> B
移动次数:3 把块:1 按照如下移动：C --> B
移动次数:4 把块:3 按照如下移动：A --> C
移动次数:5 把块:1 按照如下移动：B --> A
移动次数:6 把块:2 按照如下移动：B --> C
移动次数:7 把块:1 按照如下移动：A --> C

通过运行结果可以发现：总的移动次数为：2^n-1次；n为圆盘个数；

程序地址：https://github.com/yaowenxu/codes/blob/master/递归/汉诺塔问题.cc 

保持更新，转载请注明出处；更多内容请关注cnblogs.com/xuyaowen;

参考链接：*文中图来自于参考链接，如侵权请私信我更换；

汉诺塔的图解 如何理解汉诺塔的递归？