题目描述:
题解思路:
这是一道深搜的题目,把题目意思翻译解读后理解起来就更容易一些了。题目翻译:首先我们明确这个图是一棵树,边的权值=(边两端结点数量之差)*边的长度。
进一步翻译:我们只需要知道每条边两端节点数量分别是多少即可求解问题。那么如何计算边两端结点数量——首先选当前边上的其中一点,以该节点为根节点计算整棵树的结点数量即可。而通过深搜的方式来遍历到这些端点。
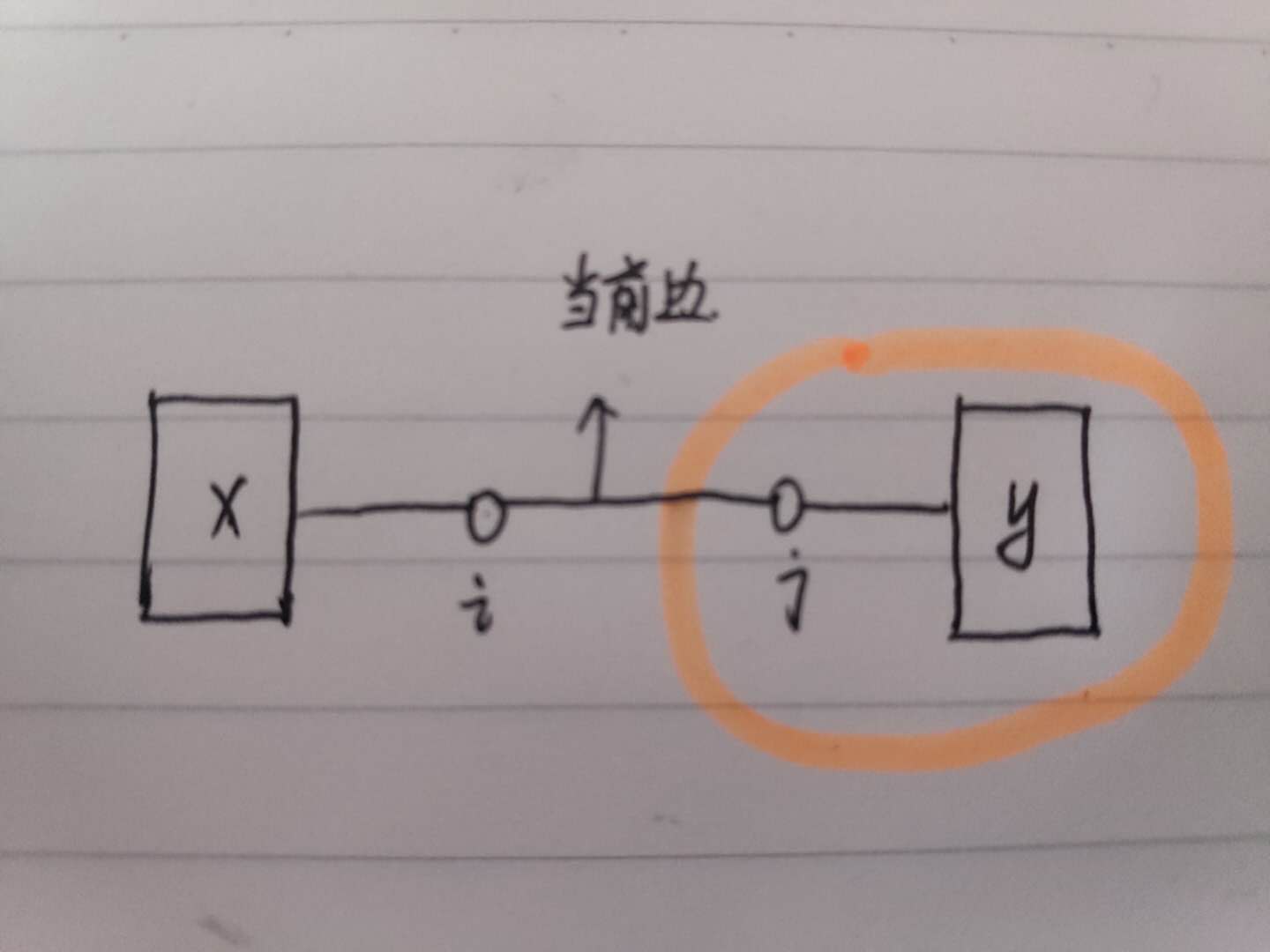
图解:以下图中i和j分别是当前边的两个端点,假设我们以点j作为根节点,那么我们需要求的结点数量就是j+Y的部分的结点个数。而另一边的结点个数则为n-(j+Y的结点个数)。但是注意,在计算j+Y 部分时,为了防止搜回到i处,加入一个状态判断要搜索的点是否为上一个刚刚搜过的点,如果搜过则直接跳过这个点。比如dfs方向从i->j,搜完i进入j搜索,在j处搜索下一个结点时不能把i列入考虑范围!
代码:
1 #include<iostream> 2 #include<cmath> 3 #include<string.h> 4 using namespace std; 5 #define re register 6 7 //由于题目里所给的数据太大,不适合用邻接矩阵存图 8 //而比较好用的存图方式有前向星(输入形式为"边起点 边终点 边权值"便可以考虑前向星) 9 struct edge{ 10 int to; //边的终点 11 int next; //下一条边的编号 12 int w; //边的权值 13 }; 14 edge e[2000001]; 15 int head[1000005]={0}; 16 int cnt=0; 17 int n; 18 int child[1000005]; //此处的child[i]代表本身加上孩子结点的数量 19 long long ans=0; //记录所有边的权值之和 20 void add(int a,int b,int c){ 21 e[cnt].to=b; 22 e[cnt].w=c; 23 e[cnt].next=head[a]; 24 head[a]=cnt; //第一条边编号更新 25 cnt++; 26 } 27 void dfs(int cur,int last){//cur代表当前结点编号,last代表cur的上一个搜索过的结点编号,dfs方向从last->cur 28 child[cur]=1; 29 int u=cur; 30 for(re int k=head[u];~k;k=e[k].next){ //点u的邻接边的遍历,k是编号 31 if(e[k].to!=last){ //因为是从last搜索过来的,不重复搜索last结点 32 dfs(e[k].to,cur); //递归边的终点 33 ans+=(long long)abs(child[e[k].to]-(n-child[e[k].to]))*e[k].w; //在搜索点的时候权值累加 34 child[cur]+=child[e[k].to]; //累加子节点个数 35 } 36 } 37 } 38 int main(){ 39 cin>>n; 40 memset(head,-1,sizeof(head)); 41 for(re int i=1;i<=n-1;i++){ 42 int a,b,c; 43 cin>>a>>b>>c; 44 add(a,b,c); //注意此处用到深搜,所以起始终止点是没有区别的 45 add(b,a,c); 46 } 47 dfs(1,0); //从点的编号1开始搜索,由于点的编号从1开始,所以假设点1的上个点搜索过的是0 48 cout<<ans; 49 return 0; 50 }