方法1:方差选择法
主要针对每个列进行计算,方差非常小的特征维度对于样本的区分作用很小,可以剔除掉。
例如:假设数据集为布尔型特征,想要去掉那些超过80%情况下为1或者为0的特征。由于布尔特征是伯努利随机变量,其方差可以计算为 Var[x] = p*(1-p),因此阈值为0.8*(1-0.8)=0.16
X= [[0,0,1],
[0,1,0],
[1,0,0],
[0,1,1],
[0,1,0],
[0,1,1],
]
第一列的方差计算为 0.14 < 0.16,因此第一个特征可以被过滤掉。
方法2:皮尔森相关系数法
皮尔森相关系数(Pearson correlation coefficient)显示两个随机变量之间线性关系的强度和方向,计算公式为:
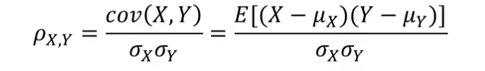
其中分子是X和Y之间的协方差,分母分别是X和Y的均方差。
计算完毕后,可以将与目标值相关性较小的特征过滤掉。
注:皮尔森相关系数对线性关系比较敏感,如果关系式非线性的,即便两个变量具有一一对应的关系,Pearson相关性也可能会接近0。
方法3:基于森林的特征选择法
其原理是某些分类器,自身提供了特征的重要性分值,因此可以直接调用这些分类器,得到特征重要性分值,并排序。
例如下图的例子中,前三个特征比较重要,其他特征分值较低。
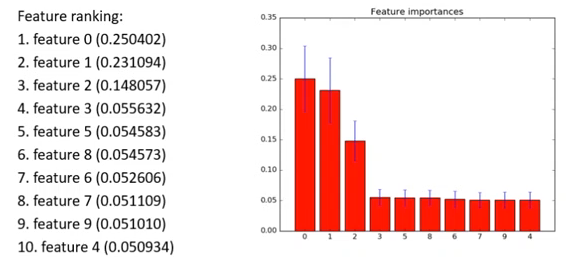
方法4:递归特征消除法
递归特征消除的基本步骤(以sklearn中的函数为例):
(1)首先在初始特征或者权重特征集合上训练,通过学习器返回的coef_属性或者feature_importances_属性来获得每个特征的重要程度。
(2)然后最小权重的特征被移除。
(3)这个过程递归进行,知道满足希望的特征数目。