字符串匹配算法

一、 朴素的串匹配算法
　　最简单的朴素匹配算法采用最直观可行的策略

•  从左到右逐个字符串匹配；
• 发现不匹配时，转去考虑目标里的下一个位置是否与模式串匹配；

　　示例：
            
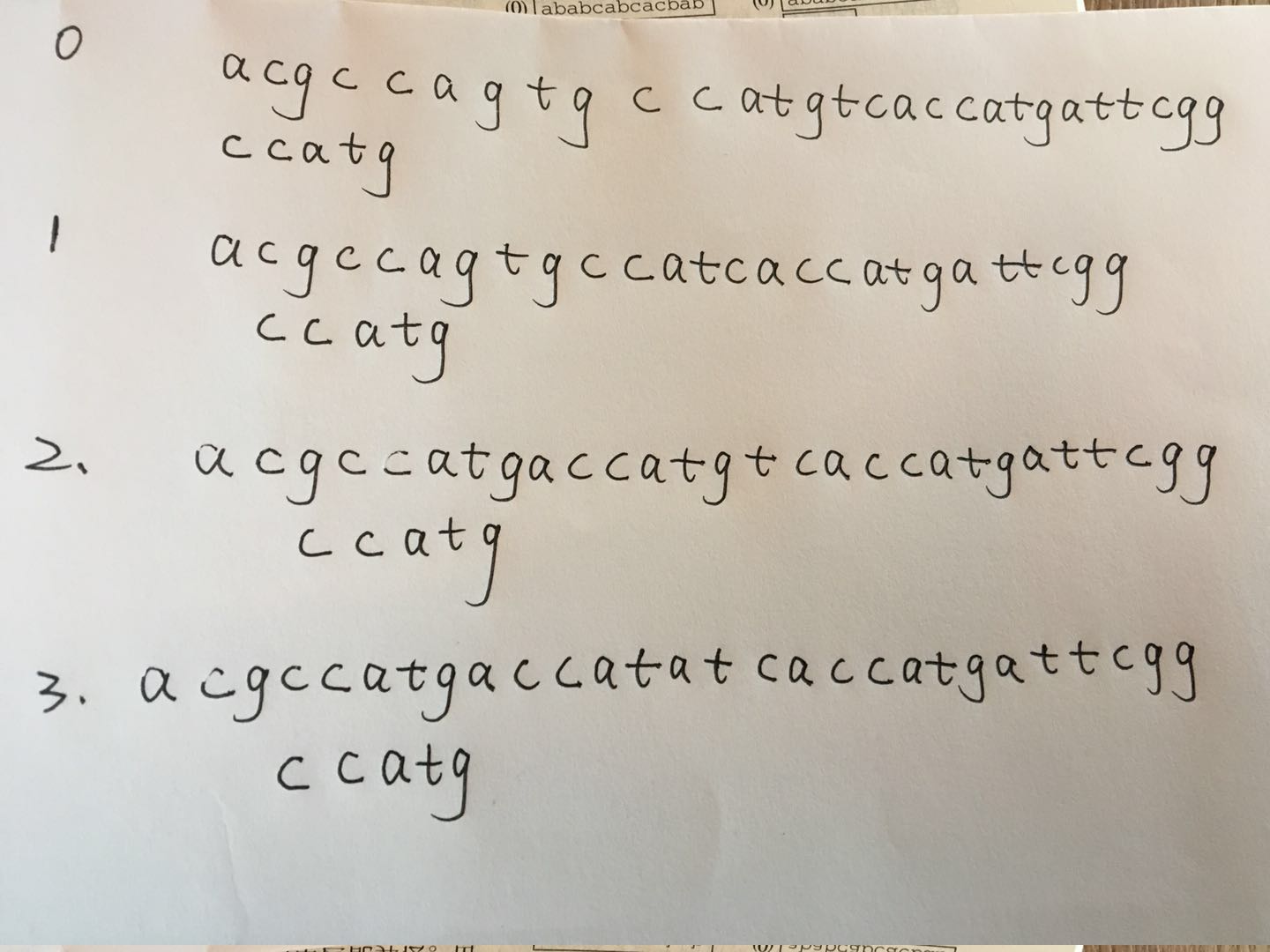
      在初始状态0：两个字符串的起始位置对齐，顺序比较，立即发现第一对字符不同。将模式串右移动一位得到位置1。顺序比较第一对字符相同，但第二对字符不同，将模式串再右移动一位，这样继续到状态3，模式串的5个字符串都与目标串对应的字符串相　　同，找到了一个匹配，继续做下去可能发现更多的匹配。

　　

def naive_matching(target, mat):
    m, n = len(target), len(mat)
    i, j = 0, 0
    while i < m and j < n:
        if mat[j] == target[i]:
            # Matched, find the next string
            i, j = i+1, j+1
        else:
            # Mismatch, match the next string of target
            i, j = i-j+1, 0
    if j == n:
        # Find match string and return index
        return i-j
    return -1

naive_matching("acgccagtgccatgtcaccatgattcgg", "ccatg")

 朴素匹配算法非常低效，主要原因是在执行过程中，可能出现回溯：匹配中遇到一个字符不同时，模式串mat将右移动一位，随后的匹配回到模式串的开始。这种算法匹配总要m-n+1趟比较。时间复杂度为O(m×n)。

二、无回溯串匹配算法
　　朴素匹配和KMP的匹配过程
      
   在朴素匹配过程中， 状态0进行匹配到模式串字符c时失败，再次进行状态1的匹配时比对目标字符串中b和模式字符串中字符a也是必然失败的，而到了状态2，模式串中的首字符a去接下来匹配目标串的b, c也是必然失败的，因此，跳过这两两个位置是没有影响的。朴素匹配没有利用到相关信息。总是在一步步移位并从头比较。
 在KMP匹配算法中，在状态0匹配字符c失败，已知前两个字符不同，KMP算法直接把模式串移动两个位置。模式串开头a移动到上一次匹配失败的c的位置，达到状态1.这次匹配知道模式串最后的c处失败，由于最后的字符c之前的字符是a，而首字符也是a, 其中间的字符是不一样的，那么可以将模式串的b移动到刚匹配出错的位置，则到了状态2.，接下来从模式串的b开始匹配。
如果先对模式串做一些分析，记录得到的有用的信息，就可能避免一些不必要的比配，提高匹配效率。KMP算法的基本想法是不回溯，在匹配失败时把模式串移到若干位置，用模式串匹配失败字符之前的某个字符与目标中匹配失败的位置比较。如果匹配中模式串p中里的某个字符$p_i$匹配目标串t的某个$t_j$时失败了，就能找到某一个特定的$k_i$,下一步用模式串中字符$p_{k_i}$与目标串的$t_j$比较。

    对于模式串p中的每一个i, 都有与之对应的下标$k_i$, 与被匹配的目标串无关。有可能通过对模式串p的分析，得到每个i对应的$k_i$, 并将其保存起来，为此可以构建pnext表，用表pnext[i]记录i对应的$k_i$值， pnext[0]=-1
　　

def matching_KMP(t, p, pnext):
    j, i = 0, 0 
    n, m = len(t), len(p)
    while j < n and i < m:
        if i == -1 or t[j] == p[i]:
            j, i = j+1, i+1
        else:
            i = pnext[i]
    if i == m:
        return j-i
    return -1

　　
   

参考： 《数据结构与算法  python语言描述》