大顶堆的实现
1.什么是堆
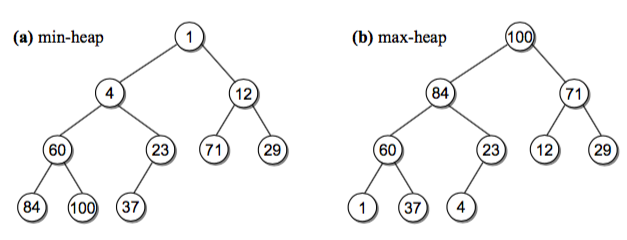
堆结构就是一种完全二叉树。堆可分为最大堆和最小堆,区别就是父节点是否大于所有子节点。最大堆的父节点大于它的子节点,而最小堆中子节点大于父节点。看图有个清晰的认识:
2. 堆的表示
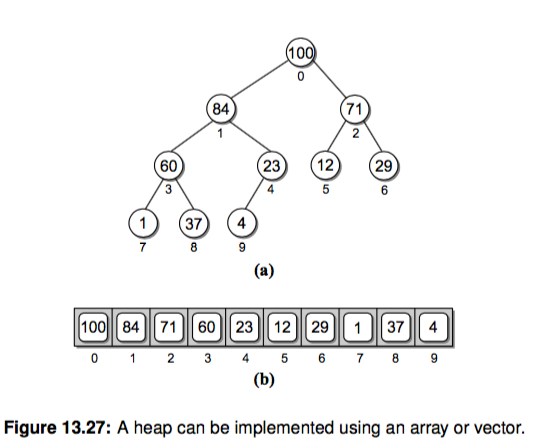
堆可以使用list实现,就是按照层序遍历顺序将每个节点上的值存放在数组中。父节点和子节点之间存在如下的关系:
1 parent = (i - 1) // 2 # 取整 2 left = 2 * i + 1 3 right = 2 * i + 2
其中i表示数组中的索引,如果left、right的值超出了数组的索引,则表示这个节点是不存在的。
3.堆的操作
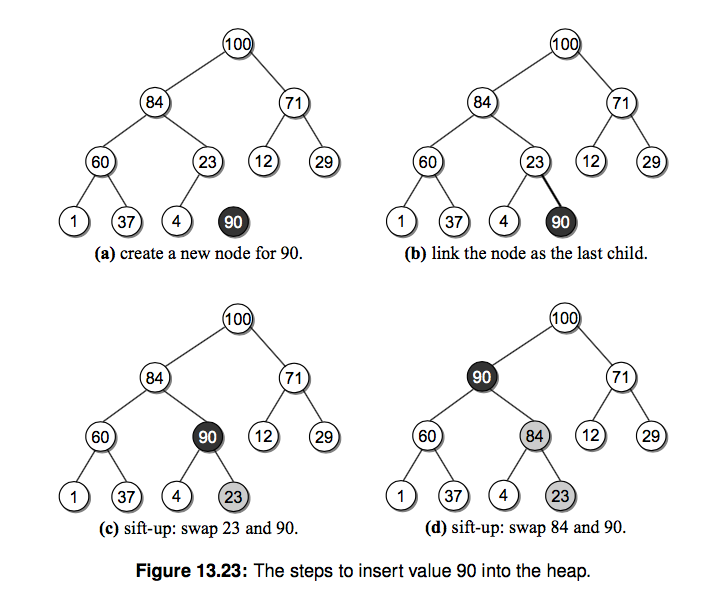
(1)往堆中插入值,sift-up操作:
往最大堆里添加一个元素,我们在使用数组实现的时候直接使用append()方法将值添加到数组的最后。这时候我们需要维持最大堆的特性,如下图。添加的新值90首先被放到堆的最后,然后与父节点的值作比较,如果比父节点值大,则交换位置。
这里涉及到的问题是子节点与父节点之间的关系。
# 堆中父节点i与子节点left、right的位置关系 parent = int((i-1) / 2) # 取整 left = 2 * i + 1 right = 2 * i + 2 # 已知子节点的位置j,求父节点的位置 parent = int((j-1)/2)
使用递归的方式,向上比较,直到根节点。
(2)获取或删除根节点,sift-down操作;
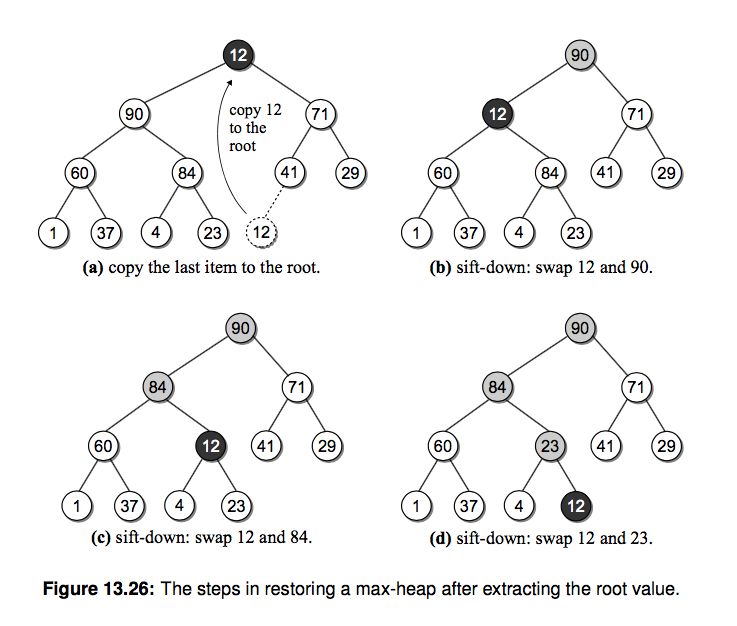
当我们把最大或者最小的值从堆中弹出,为了维持堆的特性,要使用sift-down操作。因为最大堆、最小堆的最值都在根节点,当弹出并返回根节点的值后,为了维持堆的特性,我们先将最后一个位置上的值放到根节点中。然后比较它与它的两个子节点中三个值的大小,选择最大的值放到父节点上。同理,我们这里也是使用递归的方式向下比较。这里涉及到两
个问题:
根据父节点确定子节点的位置:
left = 2 * ndx + 1
right = 2 * ndx + 2
交换位置要满足几个条件条件,比如跟左子节点交换的条件:
- 存在左子节点,
- 左子节点大于右子节点,
- 左子节点大于父节点
4. 堆的实现
代码:
1 class Array: 2 def __init__(self, size=32): 3 self.size = size 4 self._items = [None] * size 5 6 def __getitem__(self, index): 7 return self._items[index] 8 9 def __setitem__(self, index, value): 10 self._items[index] = value 11 12 def __len__(self): 13 return self.size 14 15 def clear(self): 16 for i in range(self.size): 17 self._items[i] = None 18 19 def __iter__(self): 20 for item in self._items: 21 yield item 22 23 24 class MaxHeap: 25 def __init__(self, maxsize=None): 26 self.maxsize = maxsize 27 self._elements = Array(maxsize) 28 self._count = 0 29 30 def __len__(self): 31 return self._count 32 33 def add(self, value): 34 if self._count > self.maxsize: 35 raise Exception('full') 36 self._elements[self._count] = value 37 self._count += 1 38 self._siftup(self._count - 1) 39 40 def _siftup(self, index): 41 if index > 0: 42 parent = (index - 1) // 2 43 if self._elements[index] > self._elements[parent]: 44 self._elements[index], self._elements[parent] = self._elements[parent], self._elements[index] 45 self._siftup(parent) 46 47 def extract(self): 48 if self._count == 0: 49 raise Exception('empty') 50 value = self._elements[0] 51 self._count -= 1 52 self._elements[0] = self._elements[self._count] 53 self._siftdown(0) 54 return value 55 56 def _siftdown(self, index): 57 left = 2 * index + 1 58 right = 2 * index + 2 59 largest = index 60 61 if (left < self._count and self._elements[left] >= self._elements[largest] 62 and self._elements[left] >= self._elements[right]): 63 largest = left 64 elif right < self._count and self._elements[right] >= self._elements[largest]: 65 largest = right 66 if largest != index: 67 self._elements[index], self._elements[largest] = self._elements[largest], self._elements[index] 68 self._siftdown(largest) 69 70 71 if __name__ == '__main__': 72 h = MaxHeap(12) 73 h.add(90) 74 h.add(60) 75 h.add(84) 76 h.add(1) 77 h.add(37) 78 h.add(4) 79 h.add(23) 80 h.add(71) 81 h.add(41) 82 h.add(29) 83 h.add(12) 84 for i in range(11): 85 print(h.extract())