我们规定长方形的面积是长乘上宽,其它图形的面积都必须有一个统一的度量方法,这样才有办法进行面积的比较,这个度量标准
就是矩形的面积。比如三角形的面积,相当于它所在的矩形的面积的一半,如图
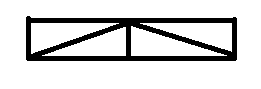
所以三角形的面积自然就是:底乘上高的面积的一半。
再比如平行四边形的面积,如图

它的面积都会等于一个矩形面积的一半,所以平行四边形的面积自然就是:底乘上高。
对于规则图形的周长就是各边的长度相加,那圆的周长呢?圆的面积怎么用矩形来度量呢?
1)圆的周长
想要知道圆的周长,可以直接通过测量的方式,找几个圆形的物体,分别量出它们的周长和直径,并计算出周长和直径的比值。通过试验和统计,
我们可以知道,圆的周长总是直径的三倍多一些,这个比值就是 $pi$。
经过统计可以发现圆的周长和半径的比值是确定的,但这个数值却无法被精确得到,普通的测量方法,得到的比值精度是有限的,到目前为止,科学家
们还在致力于圆周率的计算。圆的周长计算公式为
$$l = 2pi r$$
这个比值是通过不断地统计和测量发现的,一般取 $3.14$,这样就可以通过测量圆的半径来直接计算得到圆的周长,而不用去测量圆的周长。
2)圆的面积
圆的周长已经知道,那圆的面积如何计算呢?或者说,圆的面积如何也采用统一的度量方式来得到?
已经知道三角形的面积计算公式,我们可以由三角形的面积得到圆的面积,将圆按直径进行 $n$ 等分,每一份是一个相同的扇形,如下
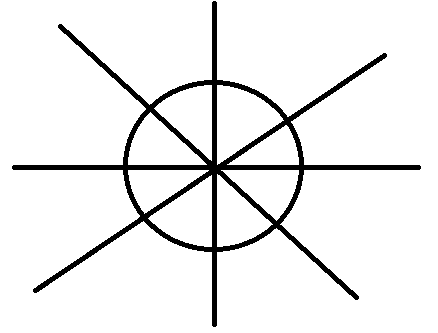
当 $n ightarrow +infty$ 时,每一个小扇形就逼近于一个等腰三角形,如图

所以,这个近似的小三角形的面积为
$$Delta S = frac{pi r^{2}}{n^{2}}sqrt{n^{2} - pi^{2}}$$
所以圆的面积为
$$S = lim_{n ightarrow +infty}n Delta S = lim_{n ightarrow +infty} frac{pi r^{2}}{n}sqrt{n^{2} - pi^{2}} = pi r^{2}$$
圆的面积本质也是用矩形的面积衡量的,需要用到逼近和极限的思想。
进一步得,我们可以得到一个扇形的面积计算公式,设一个扇形半径为 $r$,弧长为 $l$,则
$$S = pi r^{2} cdot frac{l}{2pi r} = frac{1}{2}rl$$
看起来很像三角形面积的计算公式。