这个发表于公元 $1748$ 年的数学公式,将三角函数与复指数函数巧妙地关联了起来,它长成下面这个样子
$$e^{ix} = cos x + i sin x$$
其中,$e$ 为自然常数,$i$ 为虚数,$x$ 是角度(使用弧度表示,单位 $rad$)。当参数 $x$ 等于 $pi$ 的时候,欧拉公式可简化成为:
$$e^{ipi} + 1 = 0$$
如果不了解什么是复数以及复平面,可以先去阅读博客。
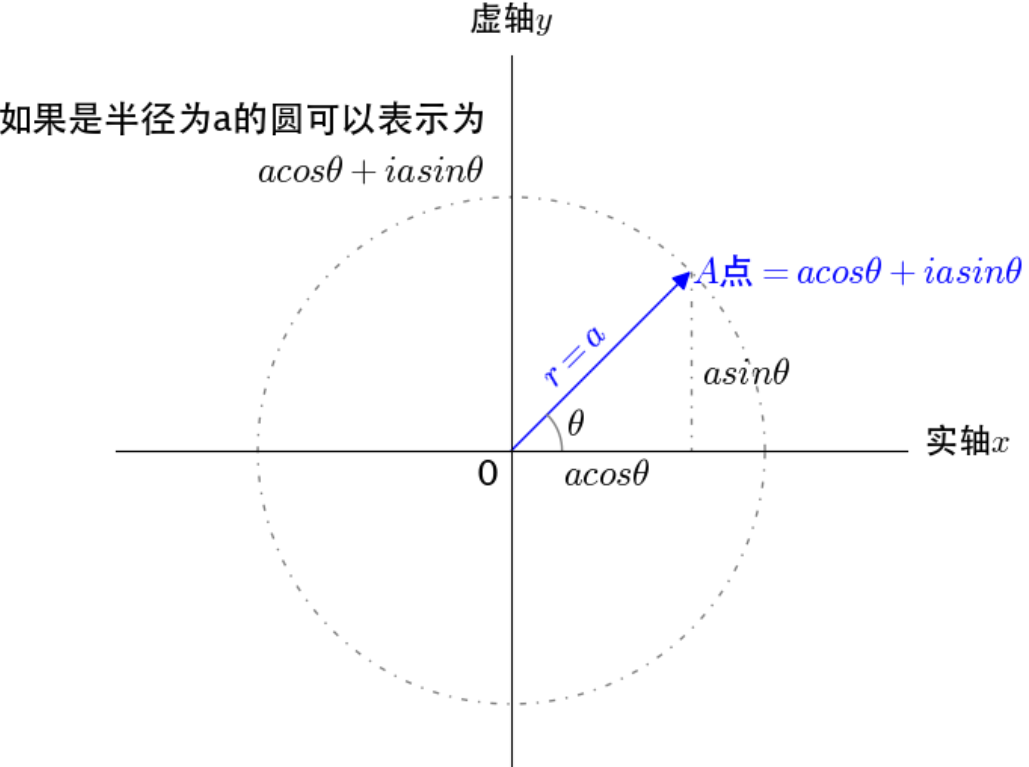
在复平面上画一个单位圆,因为三角函数的定义就是:坐标随角度变化的函数,如果不理解可以去阅读博客。所以单位圆上的点可以用三角函数
来表示为如下左图,如果半径为 $a$,则可以表示为如下右图:

欧拉最早是通过泰勒公式观察出欧拉公式:
$$e^{x} = 1 + x + frac{1}{2!}x^{2} + frac{1}{3!}x^{3} + cdots \
sin x = x - frac{1}{3!}x^{3} + frac{1}{5!}x^{5} + cdots \
cos x = 1 - frac{1}{2!}x^{2} + frac{1}{4!}x^{4} + cdots $$
将 $x = i heta$ 代入 $e^{x}$ 得
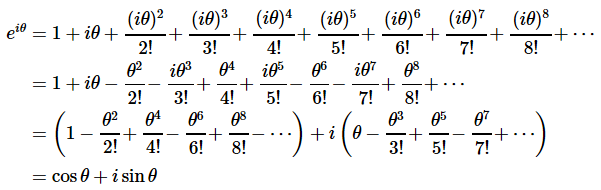
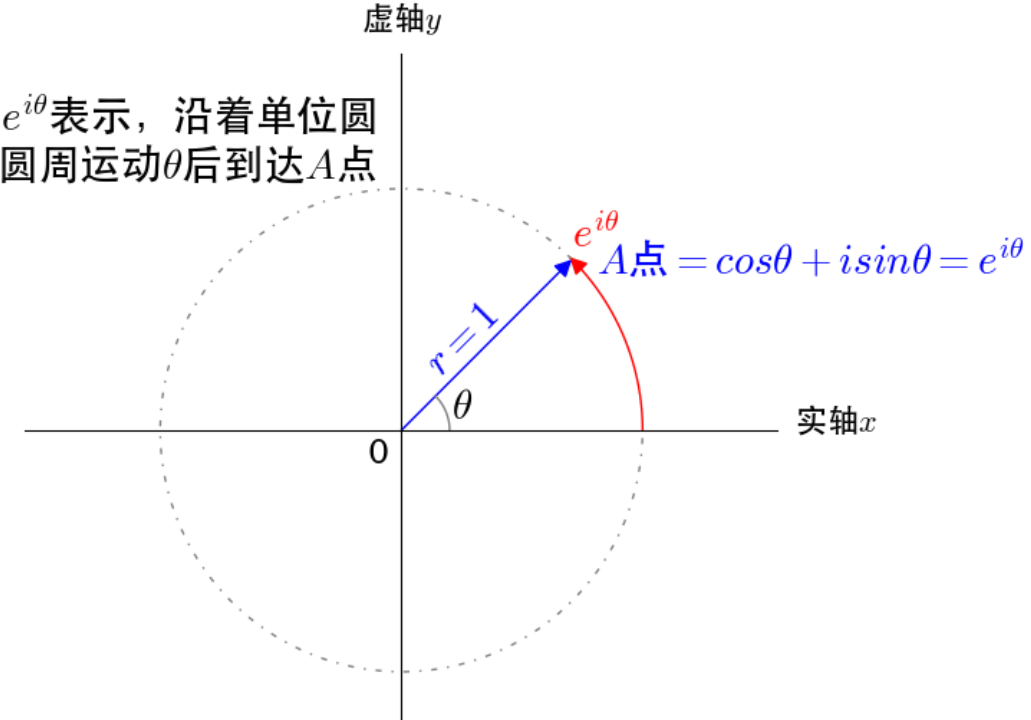
那欧拉公式怎么可以有一个直观的理解呢?先来研究一下 $e^{i heta}$ 在复平面上代表什么?其中 $ heta$ 是单位圆上的点与实轴正半轴的夹角。
在实数域上 $e$ 可以表示为极限
$$e = lim_{n ightarrow infty}left ( 1 + frac{1}{n} ight )^{n}$$
所以在实数域上
$$e^{i} = lim_{n ightarrow infty}left ( 1 + frac{i}{n} ight )^{n}$$
复数本身就是类似与向量的一种数,它的乘法会发生幅度和角度的变化,所以乘上 $1 + frac{i}{n}$ 是进行伸缩和旋转运动,$n$ 取值不同,伸缩和旋转
的幅度不同。所以 $e^{i}$ 就是表示复数 $1 + frac{i}{n}$ 做无数次乘上自身的乘法后得到的结果。
下面几个图分别表示 $n = 3$,$n = 10$,$n = 50$ 时的情况:
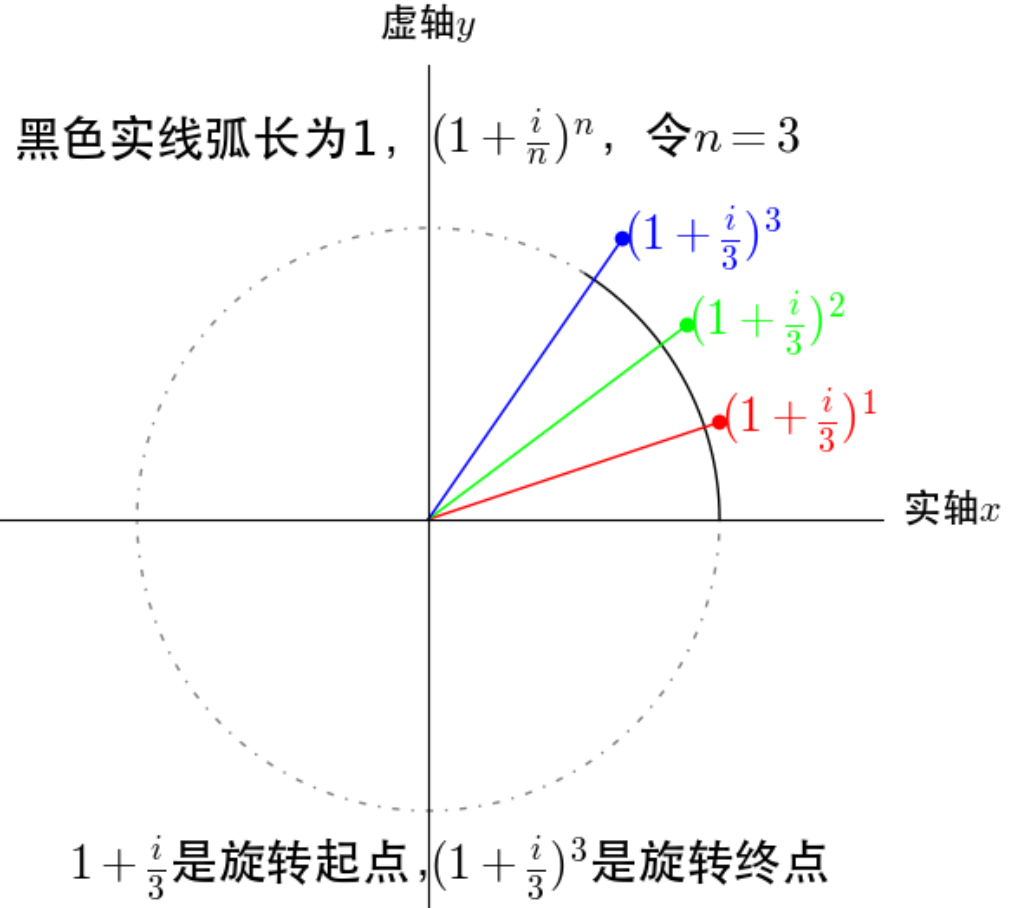
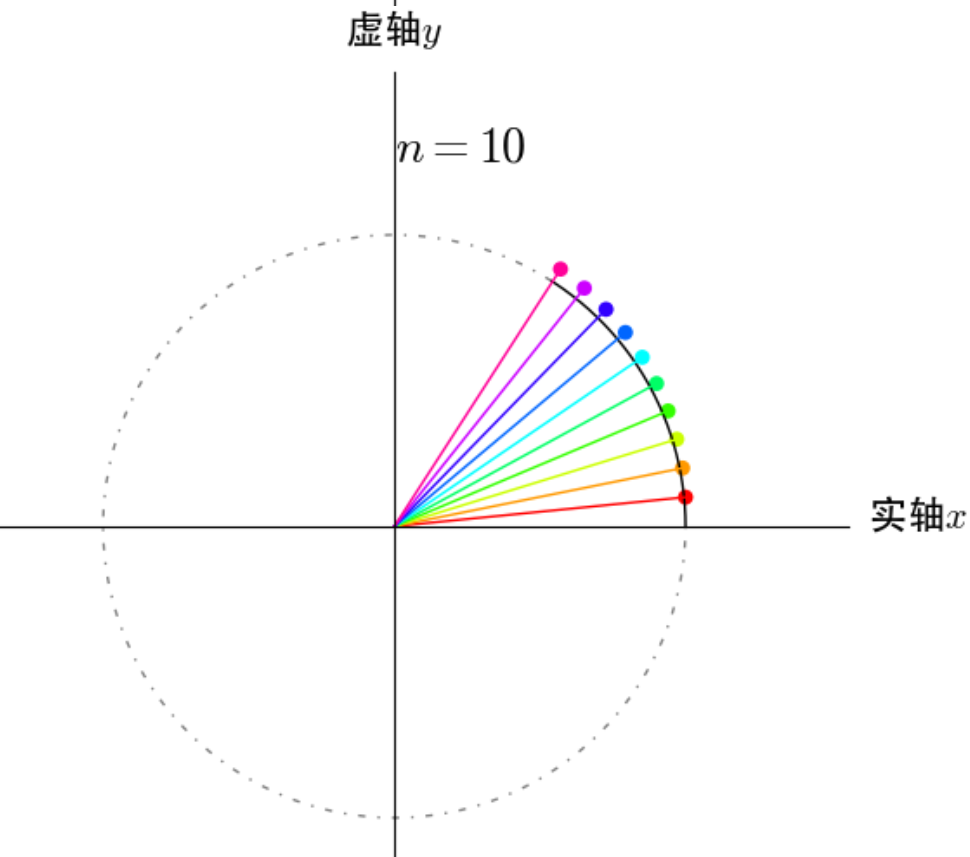
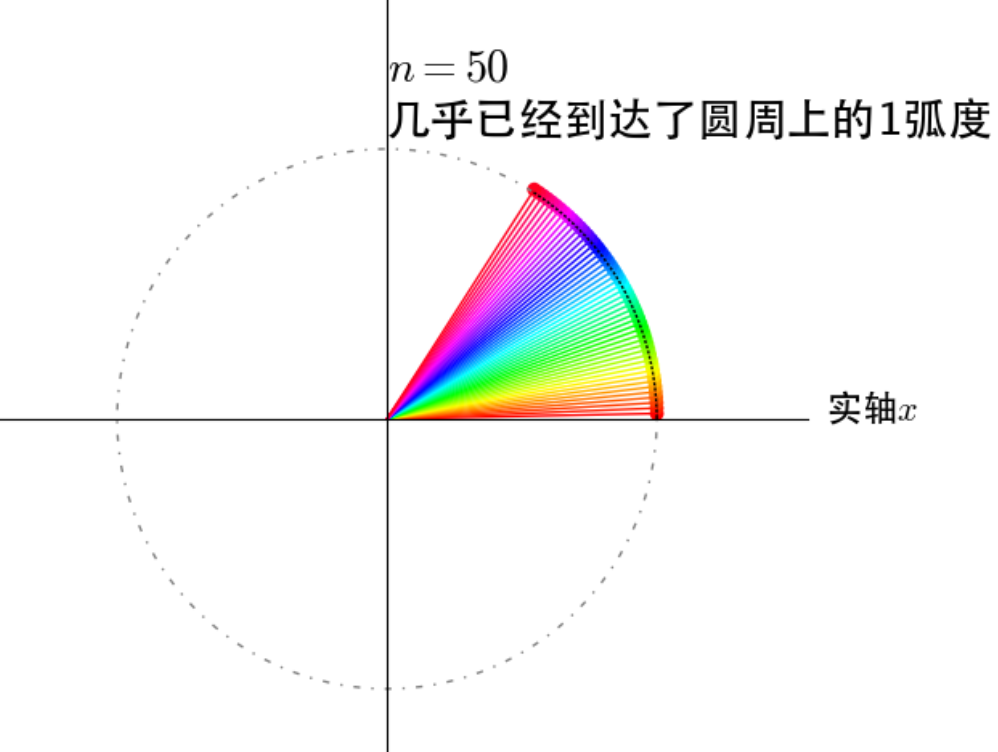
从图上可以当取极限 $n ightarrow infty$ 时,复数 $1 + frac{i}{n}$ 相当于复数 $1$,做无数次角度和幅度的变化后,复数 $lim_{n ightarrow infty}left ( 1 + frac{i}{n} ight )^{n}$
就相当于复数 $1$ 旋转了弧长为 $1$ 的距离。类似的:$e^{i heta}$ 表示复数 $1$ 在单位圆上旋转了弧长为 $ heta$ 的距离,$ae^{i heta}$ 就表示复
数 $a$ 在半径为 $a$ 的圆上旋转了弧长为 $ heta$ 的距离。逆时针还是顺时针旋转取决于 $ heta$ 的正负,为正则表示逆时针旋转。
这里没有做代数上的证明,只是通过几何直观观察的。现在回到下面这个式子
$$e^{ipi} + 1 = 0$$
是不是可以一眼看出,$e^{ipi}$ 就是复数 $1$ 逆时针旋转 180 度,得到复数 $-1$,那加上 $1$ 后自然就是 $0$ 了。
所以总结一下:$e^{i heta}$ 看作通过复数 $1$ 在单位圆上的圆周运动来描述单位圆上的点,$cos heta + i sin heta$ 通过复平面的坐标来描述单位圆上的点,
是同一个点不同的描述方式,两者自然就会相等。
根据欧拉公式可以推出
$$sin heta = frac{e^{i heta} - e^{-i heta}}{2i} \
cos heta = frac{e^{i heta} + e^{-i heta}}{2}$$
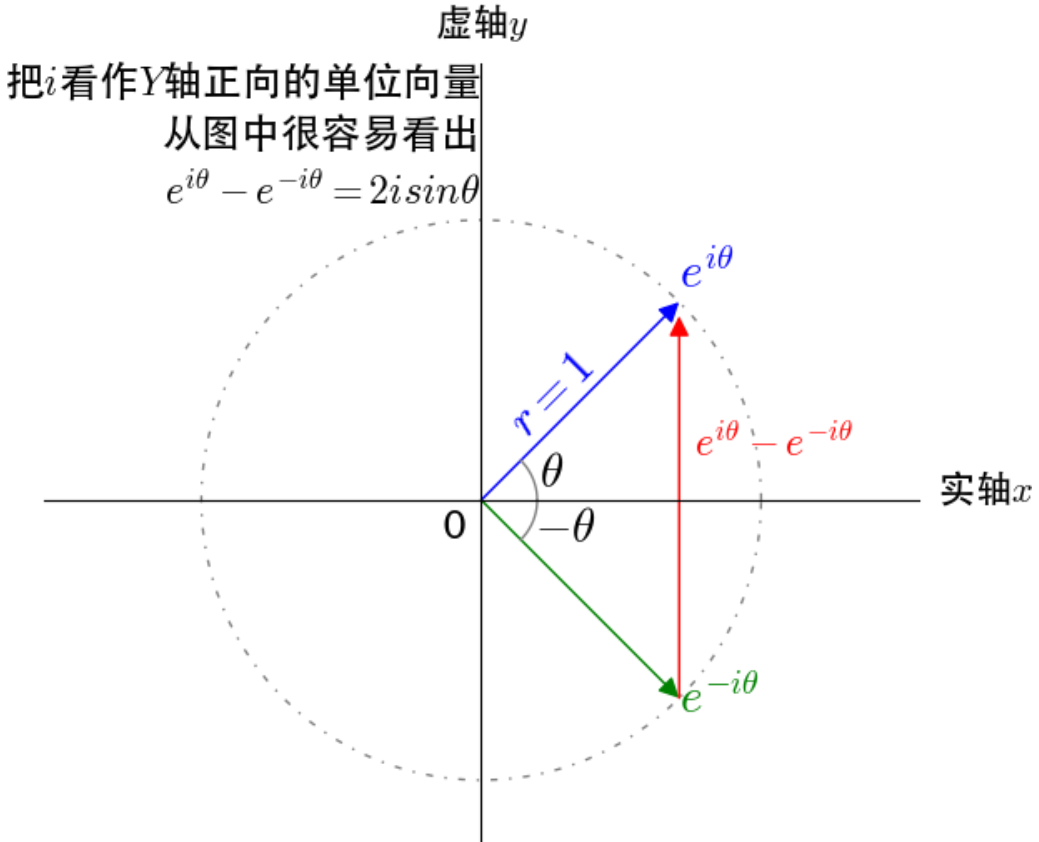
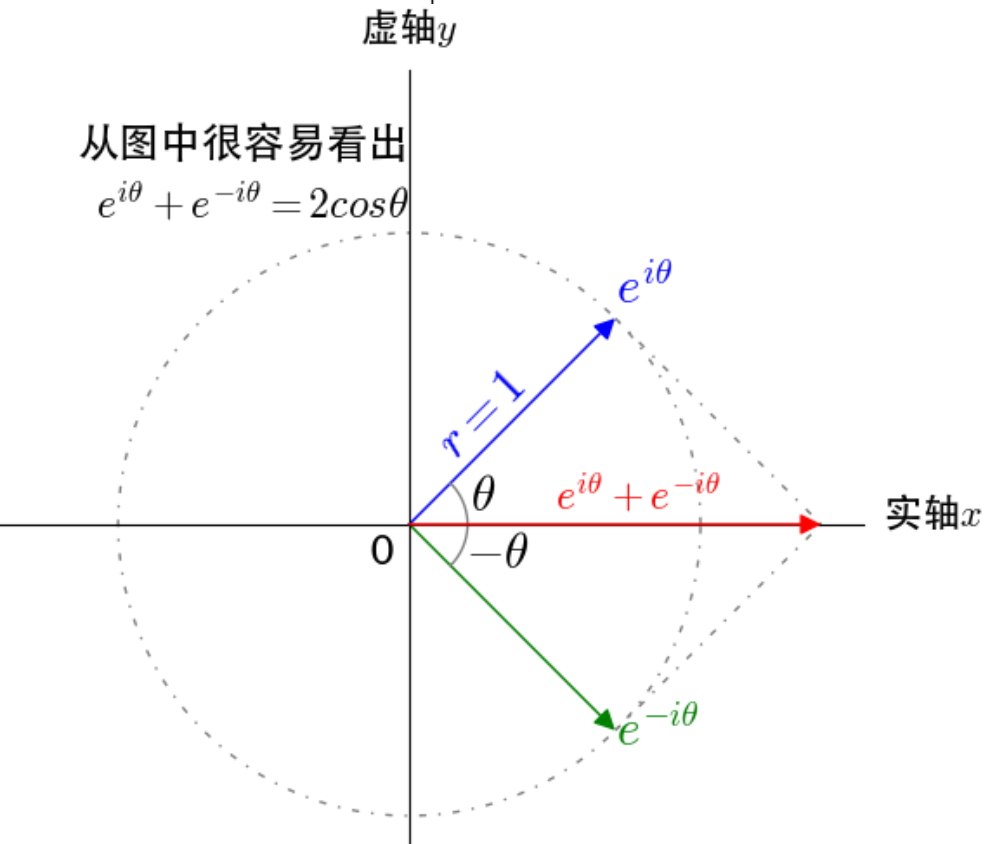
对于分子 $e^{i heta} - e^{-i heta}$ 和 $e^{i heta} + e^{-i heta}$ 都代表一个复数,当成向量来考虑,其实左图红线的位置不对,应该把起始点移到原点,但因为除了 $i$,所以没关系。