Treap讲解
上一篇blog提出了Treap这个算法,在这里我就要详细讲解。
首先,我们可以从字面上理解这个算法,Treap这个单词是由Tree和Heap两个单词构成的,所以它的性质就很好理解了,明显就是同时满足Tree和Heap两个算法的性质,那么Tree是什么呢?
Heap又是什么呢?Tree是BST,而Heap是堆,如果这两个算法不懂的话可以先学习一下,因为Treap是在这两个算法的基础上产生的,BST可以看我的上一篇博客,而Heap就只能再找了,本人比较懒,没有写,见谅。
好了言归正传,如何将BST的性质和Heap的性质结合在一起呢?似乎比较简单,我们可以在BST的基础上再开一个数组,来进行维护堆的性质,这个数组我们可以随意赋值,但是整体的数需要满足堆的性质(如左下图)。在图中的树就明显满足,val的排序方式是按照BST,而ord的排序方式是按照小根堆。这样的性质就十分靠谱,因为我每次堆ord的赋值是随机的,所以不论插入的顺序是什么,我们都可以完美的解决危机。现在问题来了,插入时找到节点了,也赋完值了,但是突然发现不满足Heap的性质了(如右下图),怎么办?
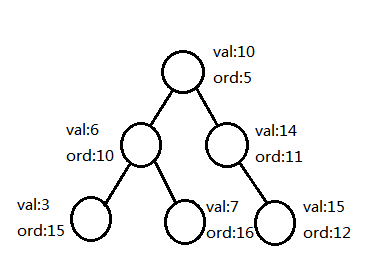
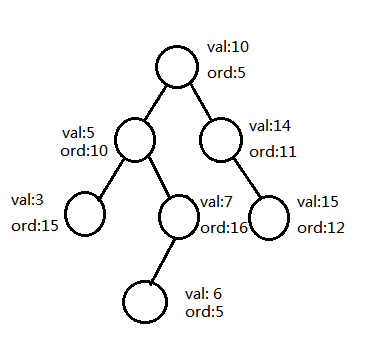
这个时候,我们就可以引出Treap的核心部分,左旋和右旋。首先讲右旋,当当前节点的左儿子的ord小于自己的时候,我们可以进行这个操作,如下图,经过这样一个小小的变换,性质就有满足了,这个转换比较好实现,我们可以直接对节点的儿子编号进行修改还就好了。
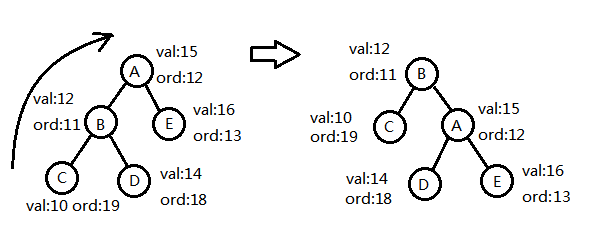

1 void rturn(int &p) 2 { 3 int tmp=lson[p]; 4 lson[p]=rson[tmp],rson[tmp]=p; 5 p=tmp; 6 } 7 //lson[p]记录p号节点的左儿子的编号 8 //rson[p]记录p号节点的右儿子的编号

1 void lturn(int &p) 2 { 3 int tmp=rson[p]; 4 rson[p]=lson[tmp],lson[tmp]=p; 5 p=tmp; 6 } 7 //lson[p]记录p号节点的左儿子的编号 8 //rson[p]记录p号节点的右儿子的编号
这是两个基本操作,只要写treap就需要用到。下面讲解一下基本操作:添加,单点删除。
添加:添加操作比较简单,首先找到只满足BST性质的位置,将其添加进Treap中,如果这是一个新节点,我们可以在上面赋值ord,这是一个随机的数值,之后就可以回溯了。当每一次回溯的时候,我们需要判断一下,是否需要左旋或者右旋,即可,是不是很简单?

1 void add(int &p,int number) 2 { 3 if(!p) 4 { 5 p=++idx,ct[p]=1,val[p]=number; 6 size[p]=1,ord[p]=rand(); 7 return; 8 } 9 size[p]++; 10 if(val[p]==number) ct[p]++; 11 else if(np<number) 12 add(rson[p],number); 13 else if(np>number) 14 add(lson[p],number); 15 if(ord[rson[p]]<ord[p]) lturn(p); 16 if(ord[lson[p]]<ord[p]) rturn(p); 17 } 18 //ct[p]记录p号节点出现的次数 19 //lson[p]记录p号节点的左儿子的编号 20 //rson[p]记录p号节点的右儿子的编号 21 //val[p]记录p号节点的权值 22 //ord[p]记录p号节点的随机值 23 //size[p]记录以p号节点为根的子树的大小 24 //number是要插入的权值
单点删除:我们首先需要查询到当前点,如果当前点的ct>1,我们可以直接ct--,如果不是,我们需要把它旋到最下面,每一次旋转都是把自己的左儿子和右儿子中ord小的点旋上来,直到把要删除的节点旋到最下面为止,直接删去它和它父亲的连边就好了。当然,有时候会出现一种情况,就是旋到当前节点只有左儿子或者右儿子,直接把当前节点的儿子提上来就好了(如图)(注:这张图片来自http://www.cnblogs.com/huangxincheng/archive/2012/07/30/2614484.html,本人较懒,就不用画图画了)
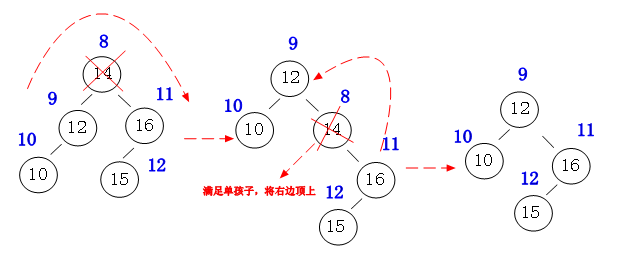

1 void del(int &p,int number) 2 { 3 if(!p) return; 4 if(val[p]==number) 5 { 6 if(ct[p]>1) 7 { 8 ct[p]--,size[p]--; 9 return; 10 } 11 if(lson[p]*rson[p]==0) p=lson[p]+rson[p]; 12 else if(ord[lson[p]]<ord[rson[p]]) 13 rturn(p),del(p,number); 14 else if(ord[rson[p]]<=ord[lson[p]]) 15 lturn(p),del(p,number); 16 return; 17 } 18 size[p]--; 19 if(val[p]<number) 20 del(rson[p],number); 21 else del(lson[p],number); 22 } 23 //ct[p]记录p号节点出现的次数 24 //lson[p]记录p号节点的左儿子的编号 25 //rson[p]记录p号节点的右儿子的编号 26 //val[p]记录p号节点的权值 27 //ord[p]记录p号节点的随机值 28 //size[p]记录以p号节点为根的子树的大小 29 //number是要插入的权值
大致就是这样,不会的可以评论发问题,我会解答。
