A more complex model does not always lead to better performance on testing data.
Because error due to both of 'bias' and 'variance'.
From training data, we can find (f^*), (f^*) is an enstimator of (hat{f})
bias (偏差) 和 variance (方差) 的直观表示:
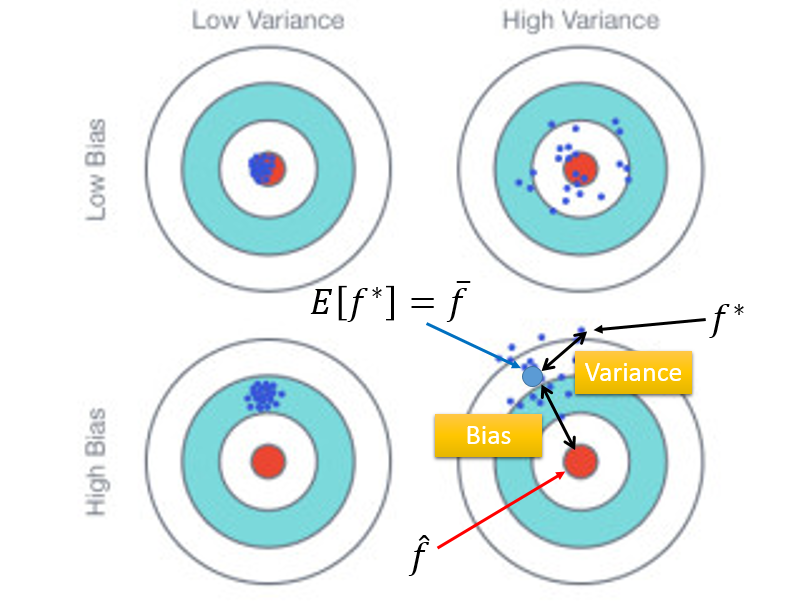
数学公式:

其中样本均值为(m),样本方差为(s^2),
总体期望为(mu),方差为(sigma^2)。
数据量很大时,(m)会逼近于(mu)。
对多个(s^2)计算期望值,这是一个有偏估计。但如果增加N的的个数,就接近于无偏估计了。

模型较简单时,容易欠拟合,bias大,variance小;
模型较复杂时,容易过拟合,bias小,variance大。

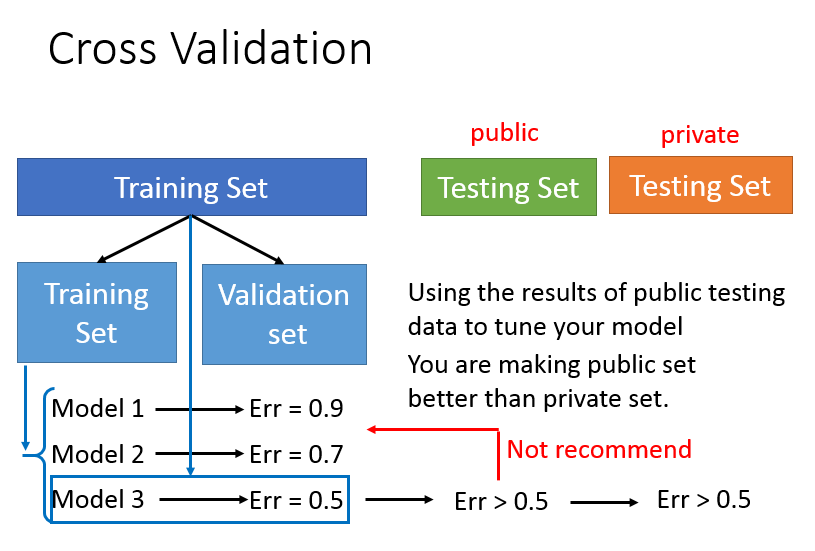
在公开数据集上取得很好的效果,在黑盒测试时,未必能取得好成绩。
可以通过增加数据量或者正则化修正。
但是数据并不太好收集,而正则化虽然variance会变小,但bias会变大,覆盖不到target。

另外的办法:将训练数据分为训练集和验证集,用不同的分法分N次,称为N折交叉验证,可以一定程度解决这个问题。