HDU 4716 A Computer Graphics Problem
水题。略
HDU 4717 The Moving Points
题目:给出n个点的起始位置以及速度矢量,问任意一个时刻使得最远的两点的距离最小。
分析:显然只有两点的话,答案满足三分性质。对于多个点,画个图分析一下,其实也满足三分性质。因此,先构造n*(n-1)/2个二次函数,于是三分枚举时间即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <map>
#include <stack>
#include <queue>
using namespace std;
#define pb push_back
#define mp make_pair
#define eps 1e-6
typedef long long ll;
struct point {
ll x, y, vx, vy;
} p[350];
struct func {
ll a, b, c;
} f[50000];
int m, n;
double anst, ansd;
inline void makef(point a, point b) {
f[m].a = (a.vx-b.vx)*(a.vx-b.vx)+(a.vy-b.vy)*(a.vy-b.vy);
f[m].b = 2*((a.x-b.x)*(a.vx-b.vx)+(a.y-b.y)*(a.vy-b.vy));
f[m++].c = (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
inline double foo(int x, double t) {
return f[x].a*t*t+f[x].b*t+f[x].c;
}
inline double getd(double t) {
double ret = -1;
for (int i = 0; i < m; ++i) {
double tmp = foo(i,t);
if (tmp > ret) ret = tmp;
}
return ret;
}
int main() {
#ifndef ONLINE_JUDGE
freopen("sum.in", "r", stdin);
// freopen("cf.out", "w", stdout);
#endif
int T;
scanf("%d", &T);
for (int ncase = 1; ncase <= T; ++ncase) {
scanf("%d", &n);
for (int i = 0; i < n; ++i)
scanf("%I64d%I64d%I64d%I64d",&p[i].x, &p[i].y, &p[i].vx, &p[i].vy);
m = 0;
for (int i = 0; i < n-1; ++i)
for (int j = i+1; j < n; ++j)
makef(p[i], p[j]);
double low = .0, high = 1e120;
while(high-low>eps) {
double mid1 = (2*low+high)/3.0;
double mid2 = (low+2*high)/3.0;
double tmp1 = getd(mid1);
double tmp2 = getd(mid2);
if (tmp1-tmp2>eps) {
anst = mid2;
ansd = tmp2;
low = mid1;
} else {
anst = mid1;
ansd = tmp1;
high = mid2;
}
}
printf("Case #%d: %.2lf %.2lf
", ncase, anst, sqrt(ansd));
}
return 0;
}
HDU 4718 The LCIS on the Tree
我用的是树链剖分+线段树来写,发现在求lca合并时很难维护,改天用lct水掉算了 >.<
这题的简单版 hdu 3308 LCIS 线段树
待补。
HDU 4719 Oh My Holy FFF
题目大意:给出n个数b1...bn,现在需要划分集合,每个集合的元素不能超过L个,并且要求第i个集合的最后一个元素now大于第i-1个集合的最后一个元素pre。每个集合的价值为:now*now-pre。题目目标是:求max{ sigma(所有集合价值) }
分析:不难想出一个递推式:dp[i]表示当前i作为集合的最后一个元素的最优解。
dp[i] = max{ dp[j] + b[i]*b[i]-b[j] }。 0<=i-j<= L,b[j]<b[i]。
注意到b[i]是不变的,于是转移方程可以写成:
dp[i] = max{ b[i]*b[i] + (dp[j] -b[j]) }。 0<=i-j<= L,b[j]<b[i]。
如何在约束( 0<=i-j<= L,b[j]<b[i] ) 下,求出dp[j]-b[j]最大?
这里可以用到单调队列,线段树维护一下即可。
具体实现(代码)献上我队友的代码吧 = =。
struct seg {
int l,r;
ll mx;
int mid() {
return l+r>>1;
};
} tree[maxn<<2];
void init_tree(int l,int r,int x)
{
tree[x].l=l,tree[x].r=r;
tree[x].mx=-1;
if(l==r)return;
int mid=l+r>>1;
init_tree(l,mid,lc(x));
init_tree(mid+1,r,rc(x));
}
void insert(int pos,int x,ll num)
{
if(tree[x].l==tree[x].r) {
tree[x].mx=num;
return;
}
int mid=tree[x].mid();
if(pos<=mid)insert(pos,lc(x),num);
else insert(pos,rc(x),num);
tree[x].mx=max(tree[lc(x)].mx,tree[rc(x)].mx);
}
ll query(int l,int r,int x)
{
if(l<=tree[x].l && tree[x].r<=r)
return tree[x].mx;
int mid=tree[x].mid();
ll res=-1;
if(l<=mid)res=max(res,query(l,r,lc(x)));
if(r>mid)res=max(res,query(l,r,rc(x)));
return res;
}
deque<pair<ll,int> >q[maxn];
int t,n,m,cas;
ll a[maxn];
int main()
{
cin>>t;
while(t--) {
scanf("%d%d",&n,&m);
init_tree(0,100000,1);
for(int i=0; i<=100000; i++)
while(!q[i].empty())q[i].pop_front();
ll ans=-1;
for(int i=1; i<=n; i++)
scanf("%I64d",&a[i]);
for(int i=1; i<=n; i++) {
ll res=query(0,a[i]-1,1);
if (i <= m && res==-1)res=0;
if(res!=-1) {
res+=a[i]*a[i];
if(i==n)ans=res;
while(!q[a[i]].empty() && q[a[i]].back().first<=res-a[i])
q[a[i]].pop_back();
q[a[i]].push_back(mp(res-a[i],i));
if(q[a[i]].front().second==i)
insert(a[i],1,q[a[i]].front().first);
}
if(i>m) {
insert(a[i-m],1,-1);
if(q[a[i-m]].size() && q[a[i-m]].front().second==i-m)
q[a[i-m]].pop_front();
if(!q[a[i-m]].empty())
insert(a[i-m],1,q[a[i-m]].front().first);
}
}
if(ans!=-1)printf("Case #%d: %I64d
",++cas,ans);
else printf("Case #%d: No solution
",++cas);
}
}
HDU 4720 Naive and Silly Muggles
注意到不一定是外接圆,如果是钝角三角形时,最长边即为直径。
#include <set>
#include <map>
#include <list>
#include <cmath>
#include <queue>
#include <stack>
#include <string>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define debug puts("here")
#define rep(i,n) for(int i=0;i<n;i++)
#define rep1(i,n) for(int i=1;i<=n;i++)
#define REP(i,a,b) for(int i=a;i<=b;i++)
#define foreach(i,vec) for(unsigned i=0;i<vec.size();i++)
#define pb push_back
#define RD(n) scanf("%d",&n)
#define RD2(x,y) scanf("%d%d",&x,&y)
#define RD3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define RD4(x,y,z,w) scanf("%d%d%d%d",&x,&y,&z,&w)
#define All(vec) vec.begin(),vec.end()
#define MP make_pair
#define PII pair<int,int>
#define PQ priority_queue
#define cmax(x,y) x = max(x,y)
#define cmin(x,y) x = min(x,y)
#define Clear(x) memset(x,0,sizeof(x))
/*
#pragma comment(linker, "/STACK:1024000000,1024000000")
int size = 256 << 20; // 256MB
char *p = (char*)malloc(size) + size;
__asm__("movl %0, %%esp
" :: "r"(p) );
*/
char IN;
bool NEG;
inline void Int(int &x) {
NEG = 0;
while(!isdigit(IN=getchar()))
if(IN=='-')NEG = 1;
x = IN-'0';
while(isdigit(IN=getchar()))
x = x*10+IN-'0';
if(NEG)x = -x;
}
inline void LL(ll &x) {
NEG = 0;
while(!isdigit(IN=getchar()))
if(IN=='-')NEG = 1;
x = IN-'0';
while(isdigit(IN=getchar()))
x = x*10+IN-'0';
if(NEG)x = -x;
}
/******** program ********************/
const double eps=1e-8;
const double PI = acos(-1.0);
double dis(double a,double b){
return a*a+b*b;
}
int dcmp(double x){
if(fabs(x)<eps)return 0;
return x>0?1:-1;
}
double ox,oy,r;
bool cc(double x1,double y1,double x2,double y2,double x3,double y3){
ox = (x1+x2)/2,oy = (y1+y2)/2;
r = dis(ox-x2,oy-y2);
if( dcmp(dis(ox-x3,oy-y3)-r)<=0 )
return true;
return false;
}
void solve(){
double x,y;
cin>>x>>y;
if(dcmp(dis(x-ox,y-oy)-r)>0)puts("Safe");
else puts("Danger");
}
int main() {
#ifndef ONLINE_JUDGE
freopen("sum.in","r",stdin);
//freopen("sum.out","w",stdout);
#endif
int Ncase = 0;
int ncase;
RD(ncase);
double x1,x2,x3,y1,y2,y3;
while(ncase--) {
cin>>x1>>y1>>x2>>y2>>x3>>y3;
printf("Case #%d: ",++Ncase);
if(cc(x1,y1,x2,y2,x3,y3))
solve();
else if(cc(x2,y2,x3,y3,x1,y1))
solve();
else if(cc(x3,y3,x1,y1,x2,y2))
solve();
else{
double k1=x2-x1,t1=y2-y1,k2=x3-x2,t2=y3-y2;
double c1=(y2*y2+x2*x2-x1*x1-y1*y1)/2.0,c2=(y3*y3+x3*x3-x2*x2-y2*y2)/2.0;
double a=(c1*t2-c2*t1)/(t2*k1-t1*k2),b=(c1*k2-c2*k1)/(t1*k2-k1*t2);
double r=(a-x1)*(a-x1)+(b-y1)*(b-y1);
cin>>x1>>y1;
double d = dis(a-x1,b-y1);
if(dcmp(d-r)>0)
puts("Safe");
else
puts("Danger");
}
}
return 0;
}
HDU 4721 Food and Productivity
待补
HDU 4722 Good Numbers
数位DP
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <map>
#include <stack>
#include <queue>
using namespace std;
#define pb push_back
#define mp make_pair
typedef long long ll;
ll f[20], a, b;
int num[20];
ll getnum(ll x) {
if (x == -1) return 0;
if (x == 0) return 1;
int len = 0;
int tmp = 0, t = 0;
while(x) {
tmp += x % 10;
num[len++] = x % 10;
x /= 10;
}
tmp -= num[0];
ll ret = 0;
for (int l = len-1; l >= 1; --l)
ret += num[l]*f[l];
for (int i = 0; i <= num[0]; ++i)
if ((tmp+i) % 10 == 0) t = 1;
return ret+t;
}
int main() {
#ifndef ONLINE_JUDGE
freopen("sum.in","r",stdin);
//freopen("sum.out","w",stdout);
#endif
f[0] = 0;
f[1] = 1;
for (int i = 2; i <= 19; ++i) f[i] = f[i-1]*10;
int T;
scanf("%d", &T);
for (int ncase = 1; ncase <= T; ++ncase) {
scanf("%I64d%I64d", &a, &b);
printf("Case #%d: %I64d
",ncase,getnum(b)-getnum(a-1));
}
return 0;
}
HDU 4723 How Long Do You Have to Draw
怎么我感觉这题不难,难道我打开的方式不对?可惜比赛时没看题。。。
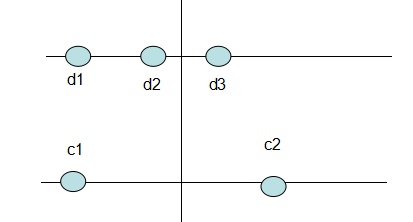
给出n个纵坐标为a的点,c1<c2<...<cn
给出m个纵坐标为b的点,d1<d2<...<dm
问如何对上下点进行连边,使得三角形最多,并且边不能相交。
分析:对于下图进行分析讨论即可。
如果c点已经到了最后,则:c点连剩下的d点
如果d点已经到了最后,则:d点连剩下的c点
如果c,d后面还有,有两种情况:
1.为c1,d1,d2在c1,c2中线左边,则c1连d1,d后移
2.为c1,d2,d3在c1,c2中线右边,则c1连d1,判断c1d3,c2d2的距离,根据那个更优移动哪个点即可。
#include <set>
#include <map>
#include <list>
#include <cmath>
#include <queue>
#include <stack>
#include <string>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define debug puts("here")
#define rep(i,n) for(int i=0;i<n;i++)
#define rep1(i,n) for(int i=1;i<=n;i++)
#define REP(i,a,b) for(int i=a;i<=b;i++)
#define foreach(i,vec) for(unsigned i=0;i<vec.size();i++)
#define pb push_back
#define RD(n) scanf("%d",&n)
#define RD2(x,y) scanf("%d%d",&x,&y)
#define RD3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define RD4(x,y,z,w) scanf("%d%d%d%d",&x,&y,&z,&w)
#define All(vec) vec.begin(),vec.end()
#define MP make_pair
#define PII pair<int,int>
#define PQ priority_queue
#define cmax(x,y) x = max(x,y)
#define cmin(x,y) x = min(x,y)
#define Clear(x) memset(x,0,sizeof(x))
/*
#pragma comment(linker, "/STACK:1024000000,1024000000")
int size = 256 << 20; // 256MB
char *p = (char*)malloc(size) + size;
__asm__("movl %0, %%esp
" :: "r"(p) );
*/
char IN;
bool NEG;
inline void Int(int &x){
NEG = 0;
while(!isdigit(IN=getchar()))
if(IN=='-')NEG = 1;
x = IN-'0';
while(isdigit(IN=getchar()))
x = x*10+IN-'0';
if(NEG)x = -x;
}
inline void LL(ll &x){
NEG = 0;
while(!isdigit(IN=getchar()))
if(IN=='-')NEG = 1;
x = IN-'0';
while(isdigit(IN=getchar()))
x = x*10+IN-'0';
if(NEG)x = -x;
}
/******** program ********************/
const int MAXN = 1e5+5;
double c[MAXN],d[MAXN],a,b;
double dis(double x,double y){
return sqrt(x*x+y*y);
}
double dis(double x1,double y1,double x2,double y2){
return dis(x1-x2,y1-y2);
}
int main(){
#ifndef ONLINE_JUDGE
freopen("sum.in","r",stdin);
//freopen("sum.out","w",stdout);
#endif
int ncase,n,m,Ncase = 0;
RD(ncase);
while(ncase--){
printf("Case #%d: ",++Ncase);
scanf("%lf%lf",&a,&b);
RD2(n,m);
rep1(i,n)
scanf("%lf",&c[i]);
rep1(i,m)
scanf("%lf",&d[i]);
double ans = 0;
int x = 1 ,y = 1;
while(x<=n&&y<=m){
if( x==n ){
ans += dis(c[x],a,d[y],b);
y ++;
}else if( y==m ){
ans += dis(c[x],a,d[y],b);
x ++;
}else{
if(d[y+1]*2<=c[x]+c[x+1]){
ans += dis(c[x],a,d[y],b);
y ++;
}else{
ans += dis(c[x],a,d[y],b);
double tmp = dis(c[x],a,d[y+1],b);
double ret = dis(c[x+1],a,d[y],b);
if(ret<tmp)
x ++;
else y++;
}
}
}
printf("%.2lf
",ans);
}
return 0;
}
HDU 4724 If You Know This,You Must Have NO GF
待补
HDU 4725 The Shortest Path in Nya Graph
使用堆维护dijkstra的算法,每次从堆中取出一个节点,如果该节点所在的层没被标记,更新相邻两层,标记上(因为每次都从堆中去最小值,因此当前层的最优值必定是第一次访问时所得,进而更新其他的层)。至于边的松弛,跟普通的dijkstra一样。详细看代码。
#include <set>
#include <map>
#include <list>
#include <cmath>
#include <queue>
#include <stack>
#include <string>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define debug puts("here")
#define rep(i,n) for(int i=0;i<n;i++)
#define rep1(i,n) for(int i=1;i<=n;i++)
#define REP(i,a,b) for(int i=a;i<=b;i++)
#define foreach(i,vec) for(unsigned i=0;i<vec.size();i++)
#define pb push_back
#define RD(n) scanf("%d",&n)
#define RD2(x,y) scanf("%d%d",&x,&y)
#define RD3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define RD4(x,y,z,w) scanf("%d%d%d%d",&x,&y,&z,&w)
#define All(vec) vec.begin(),vec.end()
#define MP make_pair
#define PII pair<int,int>
#define PQ priority_queue
#define cmax(x,y) x = max(x,y)
#define cmin(x,y) x = min(x,y)
#define Clear(x) memset(x,0,sizeof(x))
/*
#pragma comment(linker, "/STACK:1024000000,1024000000")
int size = 256 << 20; // 256MB
char *p = (char*)malloc(size) + size;
__asm__("movl %0, %%esp
" :: "r"(p) );
*/
char IN;
bool NEG;
inline void Int(int &x){
NEG = 0;
while(!isdigit(IN=getchar()))
if(IN=='-')NEG = 1;
x = IN-'0';
while(isdigit(IN=getchar()))
x = x*10+IN-'0';
if(NEG)x = -x;
}
inline void LL(ll &x){
NEG = 0;
while(!isdigit(IN=getchar()))
if(IN=='-')NEG = 1;
x = IN-'0';
while(isdigit(IN=getchar()))
x = x*10+IN-'0';
if(NEG)x = -x;
}
/******** program ********************/
const int MAXN = 1e5+5;
const int INF = 1e9+7;
struct Edge{
int y,cost,next;
}edge[MAXN<<1];
int po[MAXN],tol;
vector<int> vec[MAXN];
int la[MAXN],n,per,m;
int dis[MAXN];
bool use[MAXN];
bool ok[MAXN];
struct node{
int x,cost;
friend bool operator < (node a,node b){
return a.cost>b.cost;
}
node(){}
node(int _x,int _cost):x(_x),cost(_cost){}
};
int dijkstra(){
priority_queue<node> q;
Clear(use);
rep1(i,n)dis[i] = INF;
q.push(node(1,0));
dis[1] = 0;
Clear(ok);
while(!q.empty()){
node p = q.top();
q.pop();
int x = p.x;
if(use[x])continue;
use[x] = 1;
if(x==n&&dis[n]<INF)break;
if(!ok[la[x]]){
ok[la[x]] = 1;
int now = la[x]-1;
if(now)
foreach(i,vec[now]){
int y = vec[now][i];
if(!use[y]&&dis[x]+per<dis[y]){
dis[y] = dis[x]+per;
q.push(node(y,dis[y]));
}
}
now += 2;
if(now<=n)
foreach(i,vec[now]){
int y = vec[now][i];
if(!use[y]&&dis[x]+per<dis[y]){
dis[y] = dis[x]+per;
q.push(node(y,dis[y]));
}
}
}
for(int i=po[x];i;i=edge[i].next){
int y = edge[i].y;
int tmp = edge[i].cost+dis[x];
if(!use[y]&&tmp<dis[y]){
dis[y] = tmp;
q.push(node(y,dis[y]));
}
}
}
return dis[n];
}
inline void add(int x,int y,int cost){
edge[++tol].y = y;
edge[tol].cost = cost;
edge[tol].next = po[x];
po[x] = tol;
}
int main(){
#ifndef ONLINE_JUDGE
freopen("cf.in","r",stdin);
//freopen("sum.out","w",stdout);
#endif
int x,y,c,ncase,Ncase = 0;
RD(ncase);
while(ncase--){
printf("Case #%d: ",++Ncase);
RD3(n,m,per);
rep1(i,n)
vec[i].clear();
rep1(i,n){
RD(la[i]);
vec[la[i]].pb(i);
}
Clear(po);
tol = 0;
while(m--){
RD3(x,y,c);
add(x,y,c);
add(y,x,c);
}
int ans = dijkstra();
printf("%d
",ans==INF?-1:ans);
}
return 0;
}
HDU 4726 Kia's Calculation
贪心。第一位想清楚了,后面的直接贪心。略
HDU 4727 The Number Off of FFF
水题。注意全对时输出1。略