数据结构：哈夫曼树和哈夫曼编码

哈夫曼树

哈夫曼树是一种最优二叉树，其定义是：给定n个权值作为n个叶子节点，构造一棵二叉树，若树的带权路径长度达到最小，这样的树就达到最优二叉树，也就是哈夫曼树，示例图如下：

基本概念

深入学习哈夫曼树前，先了解一下基本概念，并以上面的哈夫曼树图为例

• 路径：树中一个结点到另一个结点之间的分支序列构成两个结点间的路径。
• 路径长度：路径中分支的数目，从根结点到第L层结点的路径长度为L-1。例如100和80的路径长度为1，50和30的路径长度为2。
• 结点的权：树中结点的数值，例如100，50那些。
• 结点带权路径长度：根结点到该结点之间的路径长度与该结点的权的乘积。 如结点20的路径长度为3，该结点的带权路径长度为：3*20 = 60。
• 树的带权路径长度：所有叶子结点的带权路径长度之和，记为WPL。例如上图树的WPL = 1100 + 280 +320 +310 = 350。

带权路径长度比较

前面说到，哈夫曼树是最优二叉树，因为符合哈夫曼树特点的树的带权路径长度一定是最小的，我们将哈夫曼树和普通的二叉树做个比较，仍以上图为例，上图的哈夫曼树是结点10，20，50，100组成的二叉树，WPL是350，用这四个结点组成普通的二叉树，结果如下：

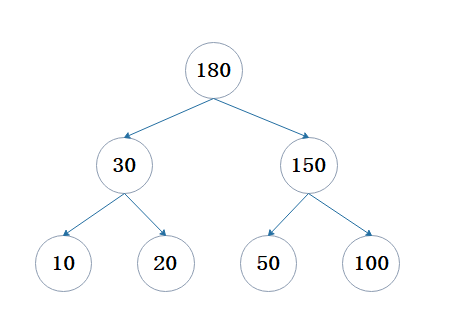
不难计算，该二叉树的WPL = 210 + 220 + 250 + 2100 = 360，明显比哈夫曼树大，当然二叉树的组成结果不唯一，但WPL一定比哈夫曼树大。所以说哈夫曼树是最优二叉树。

哈夫曼树的构造

现在假定有n个权值，设为w1、w2、…、wn，将这n个权值看成是有n棵树的森林，根据最小带权路径长度的原则，我们可以按照下面步骤来将森林构造成哈夫曼树：

1. 在森林中选出根结点的权值最小的两棵树进行合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；
2. 从森林中删除选取的两棵树，并将新树加入森林；
3. 重复1、2步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

以森林 (16，20，23，24，50) 为例，其构造步骤如下：

① 合并权值为16和20的树，构成权值为36的新树，森林变为（36，23，24，50）;

② 合并最小的两棵树23和24，组成新的树47，这时森林变为（36，47，50）；

③ 合并36和47的树作为权值83的新树，并和50结合组成根节点权值为133的哈夫曼树。

最终结果图如下：

哈夫曼编码

哈夫曼是一种无前缀编码，使用一种特别的方法为信号源中的每个符号设定二进制码，解码时不会混淆。其主要应用在数据压缩，加密解密等场合。可以与哈夫曼树进行结合生成。

给哈夫曼树的根节点分配比特0，左子树分配0，右字数分配1，一直递归下去，然后就可以得到符号的码值了。假设我有A,B,C,D,E五个字符，出现的频率（即权值）分别为5,4,3,2,1。

这样结点对应的编码为：16 - > 100，20 - > 101，23 - > 110，24 - > 111，50 - > 0