能不能用向量来表示直线呢?
如果给定一个直线的方向向量是n=(1,1),可以求出无数条和平行的直线方程,解并不唯一。
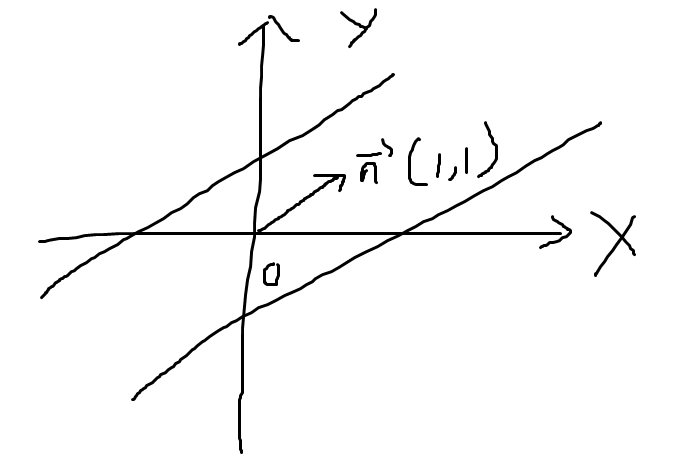
那怎么才能让某条直线固定下来呢?还需要一个点,对不对,方向向量是确定了这条直线的倾斜角,只要再经过一个定点,那么这条直线就唯一被确定了。
所以可以肯定,如果给定一条直线一个定点,和它的方向向量,就一定能唯一确定一条直线。
设一条直线过定点P0(x0,y0),它的方向向量是pdir(m,n),求这条直线的表达式?
直线是由点构成的,求直线的表达式,也就是求这条直线任意一点的坐标,我们设这条直线上任意一点坐标为p(x,y)
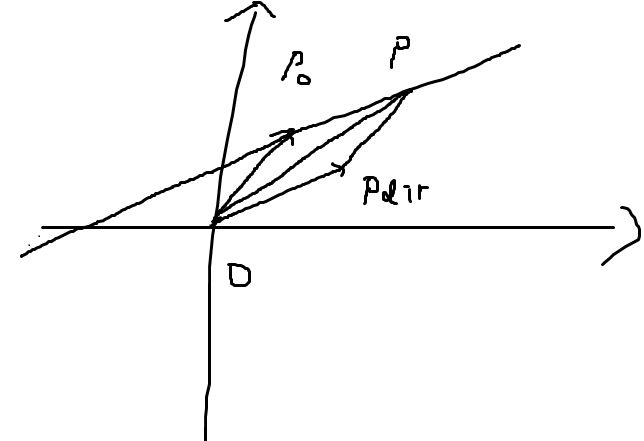
根据向量加法的四边形法则有
向量OP=向量OP0+向量OPdir,因为P0是定点,Pdir给定的话,也是定下来了,最后求出的P点坐标也是直线上的某一个点,并不能代表所有的点,怎么办?
给向量OPdir加一个参数t,就变成了
向量OP=向量OP0+t*向量OPdir
其实这就是直线的参数方程了。
简写成P=P0+tPdir
转换成坐标就是
(x,y)=(x0,y0)+t(m,n)
即
x=x0+tm
y=y0+tn
考虑一下t的范围,如果t大于0,最终表示的是点或者向量是和op向量大概是同向的),如果t<0,最终表示的点是op向量大概是反向的,如果t等于0,那么表示过定点(x0,y0)
所以t的范围应该是R
高中学习的直线的参数方程其实和这个思路是一样的。它用的是定点和直线和x轴的夹角来确定直线方程的,其实是殊途同归的。
因为直线和x轴的夹角就代表了直线的方向向量。