三维空间由3个轴组成，所以一个空间点的位置可以由3个坐标指定。但考虑刚体时，它不仅有位置，还有自身的姿态。借助数学语言，我们可以更好地来描述它。
3.1.1 点和向量，坐标系
点和向量
向量：线性空间中的一个元素，可以把它想象成从原点指向某处的一个箭头。
注意：不要混淆向量和坐标两个概念，只有在指定这个三维空间中的某个坐标系时，才可以谈论该向量在此坐标下的坐标。
如果确定了一个坐标系，也就是一个线性空间的基（e1,e2,e3），那么就可以谈论向量a在这组基下的坐标。
坐标的具体取值，一是和向量本身有关，二是和坐标系的选取有关。
对于a和b∈R3，内积可以写成：
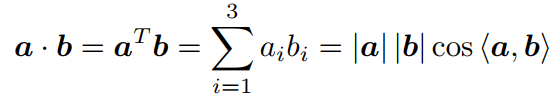
内积可以描述向量间的投影关系。
外积：
外积的方向垂直于这两个向量，大小为
，是两个向量张成的四边形的有向面积。
外积只对三维向量存在定义，我们还能用外积表示向量的旋转。
坐标间的欧氏变换
与向量间的旋转类似，同样可以描述两个坐标间的旋转关系，再加上平移，统称为坐标系间的变换关系。
举例：
在机器人的运动过程中，常见的做法是设定一个惯性坐标（或者叫世界坐标系），可认为它是固定不动的，如下图定义的坐标系。同时，相机或机器人则是一个移动坐标系。
相机视野中某个向量p,它的坐标为Pc，在世界坐标系下看，它的坐标是Pw。这两者转换：先得到该点针对机器人坐标系的坐标值，再根据机器人位姿转换到世界坐标系中，这个转换关系由一个矩阵T来描述。
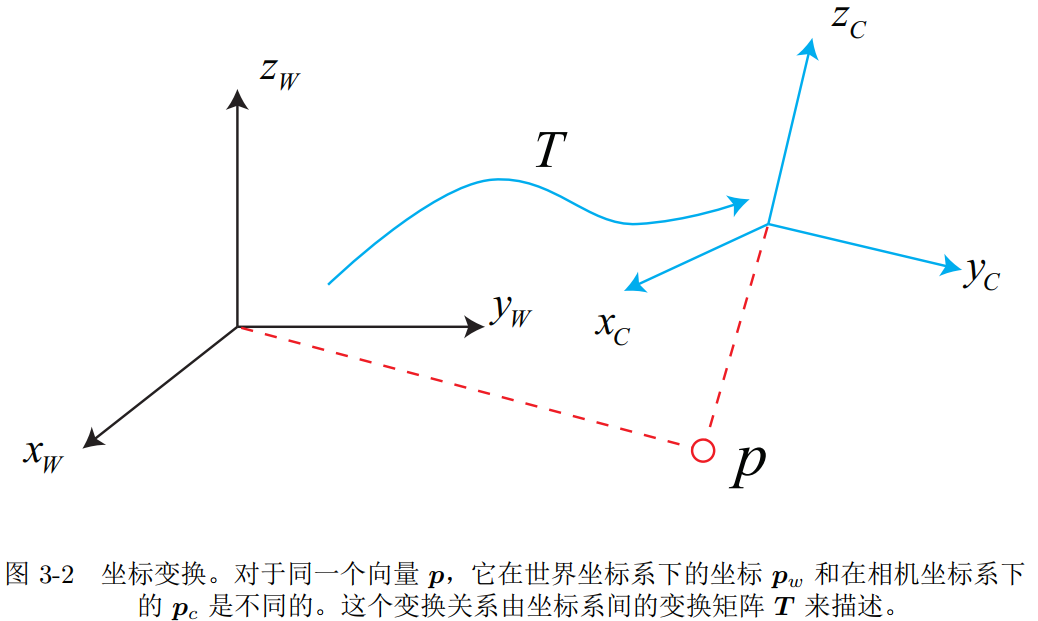
相机运动是一个刚体运动，它保证了同一个向量在各个坐标系下的长度和夹角都不会发生变化。这种变换称为欧氏变换。
欧氏变换由一个旋转和一个平移两部分组成。
首先，考虑旋转。
设某个单位正交基（e1,e2,e3）经过一次旋转变成了
。那么，对于同一个向量a（注意:该向量并没有随着坐标系的旋转而发生运动），它在两个坐标系下的坐标为
。根据坐标的定义，有：
，
为了描述两个坐标之间的关系，等式两边同时左乘
，得：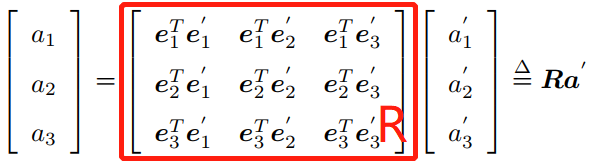
R由两组基之间得内积组成，刻画旋转前后同一个向量得坐标变换关系。矩阵R描述了旋转本身，因此称为旋转矩阵。
旋转矩阵有一些特别的性质：事实上，它是一个行列式为1的正交矩阵。反之，行列式为1的正交矩阵也是一个旋转矩阵。因此，旋转矩阵的集合定义如下：
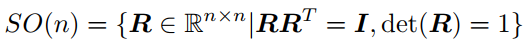
SO(n)是特殊正交群(Special Orthogonal Group)，这个集合由n维空间的旋转矩阵组成，特别的，SO(3)是三维空间的旋转。通过这个旋转可以直接讨论两个坐标系之间的旋转变换，而
不用再从基谈起。换句话说，旋转矩阵可以描述相机的旋转。
由于旋转矩阵是正交矩阵，它的逆（即转置）描述了一个相反的旋转，
在欧氏变换中，除了旋转之外还有平移。考虑世界坐标系中的向量a，经过一次旋转（用R描述）和一次平移t后，得到了a'，把旋转和平移合到一起，有：
t称为平移向量。通过上式，用一个旋转矩阵R和一个平移向量t完整地描述了一个欧氏空间的坐标变换关系。
3.1.3 变换矩阵与齐次坐标
假设进行两次变换：R1，t1和R2，t2，满足
，
从a 变换到c：
这样的形式在变换多次后会过于复杂，因此，我们引入齐次坐标和变换矩阵：
这是一个数学技巧：在一个三维向量的末尾添加1，将其变成了四维向量，称为齐次坐标。
对于这个四维向量，我们可以把旋转和平移写在一个矩阵里面，使得整个关系变成线性关系。该式中，T称为变换矩阵（Transform Matrix）。
关于变换矩阵T，它有比较特别的结构：左上角为旋转矩阵，右侧为平移向量，左下角为0向量，右下角为1。这种矩阵又称为特殊欧氏群（Special Euclidean Group）.
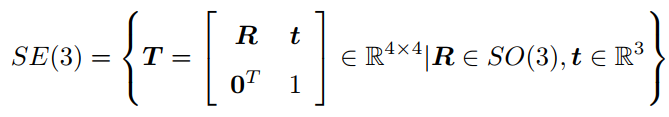
齐次坐标，是射影几何的概念。通过添加最后一维，我们用4个实数描述了一个三维向量，这显然多了一个自由度，但允许我们把变换写成线性的形式。
在齐次坐标中，某个点x的每个分量同乘一个非零常数k后，仍然表示同一个点。因此，一个点的具体坐标值不是唯一的。
但最后一项不为零时，我们总可以除以最后一项，强制最后一项为1，从而得到一个点唯一的坐标表示（也就是转换为非齐次坐标）：
