Java数据结构

Java算法与数据结构学习

此文章涉及到的代码及测试类详见我的GitHub：https://github.com/Loserfromlazy/java_data_structure_demo

大部分图片均为自己手画（个别有水印），小部分来源于百度百科

一.数组

//声明数组
dataType[] arrayRefVar;
//创建数组
arrayRefVar = new dataType[arraySize];
dataType[] arrayRefVar = new dataType[arraySize];
dataType[] arrayRefVar = {value0, value1, ..., valuek};

1.使用自定义类封装数组

public class MyArray{
    private long [] arr;
    //表示数组的有效数据的长度
    private int elements;
    public MyArray(){
        arr =new long [50];
    }
    public MyArray(int maxsize){
        arr =new long[maxsize];
    }
    /**
     * 添加数据
     */
    public void insert(long value){
        arr[elements] =value;
        elemenet++;
    }
    /**
     * 显示数据
     */
    public void display(){
        System.out.println("[");
        for(int i=0;i<elements;i++){
            System.out.println(arr[i]+"  ");
        }
        System.out.println("]");
    }
    /**
     * 根据值查找数据
     */
    public int search(long value){
        int i;
        //顺序搜索
        for(i=0;i<elements;i++){
            if(value==arr[i]){
                break;
            }
        }
        if(i==elements){
            return -1;
        }else{
            return i;
        }
    }
    /**
     * 根据索引查找数据
     */
    public long get(int index){
        if(index>=elements ||index <0){
            throw new ArrayIndexOutOfBoundsException();
        }else{
            return arr[index];
        }
    }
    /**
     * 删除数据
     */
    public void delete(int index){
        if(index>=elements ||index <0){
            throw new ArrayIndexOutOfBoundsException();
        }else{
            //将之后的数据向前一位进行覆盖
           for(int i=0;i<elements;i++){
               arr[index]=arr[index+1];
           }
            elements--;
        }
    }
    /**
     * 更新数据
     */
    public void update(int index,long newvalue){
        if(index>=elements ||index <0){
            throw new ArrayIndexOutOfBoundsException();
        }else{
           for(int i=0;i<elements;i++){
               arr[index]=newvalue;
           }
        }
    }
}

2.有序数组

修改上面的添加方法

    /**
     * 添加数据
     */
    public void insert(long value){
        int i;
        for(i=0;i<elements;i++){
            if(arr[i]>value){//找到比新加的值大的那个数的索引号i
                break;
            }
        }
        //将第i位空出，每一位向后面挪一位
        for(int j=elements;j>i;j--){
            arr[j]=arr[j-1];
        }
        //将新插入的值放入该索引的位置
        arr[i]=value;
        elements++;
    }

3.查找算法

线性查找（从头查到尾）

见上面的查找方法

二分法查找（数组必须是有序数组）

	/**
     * 二分法查找数据
     */
	public int binarySearch(long value){
        int middle=0;
        int low=0;//第一位索引
        int pow=elements;//最后一位索引
        while(true){
            middle=(pow+low)/2;
            if(arr[middle]==value){
                return middle;
            }else if(low >pow){//如果第一位索引大于最后一位的索引，代表搜索结束，没有找到该值
                return -1;
            }else{
                if(arr[middle]>value){
		//如果中间的值比查的值大，说明待查值在前面，所以将最后一位的索引改为中间的索引的前一位
                    pow=middle-1;
                }else{
        //如果中间的值比查的值小，说明待查值在后面，所以将第一位的索引改为中间的索引的后一位
                    low=middle+1;
                }
            }
        }
    }

二.简单排序

1.冒泡排序

它重复地走访过要排序的元素列，依次比较两个相邻的元素，如果顺序（如从大到小、首字母从Z到A）错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换，也就是说该元素列已经排序完成。下面这个动图来自郭耀华's Blog（不会做动图，这动图做的太好了）

    /**
	 * 冒泡排序
	 * @param arr
	 */
	public static void sort(long arr[]) {
		long tmp=0;
		for (int i = 0; i < arr.length-1; i++) {//遍历数组
			//依次比较两个相邻的元素，并交换
            for (int j = arr.length-1; j >i; j--) {
				if(arr[j]<arr[j-1]) {
					tmp=arr[j];
					arr[j]=arr[j-1];
					arr[j-1]=tmp;
				}
			}
		}
	}

2.选择排序

第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。

效率比冒泡排序高一些

下面这个动图来自郭耀华's Blog（不会做动图，这动图做的太好了）

	/**
	 * 选择排序
	 * @param arr
	 */
	public static void sort(long[] arr) {
		int k=0;
		long tmp=0;//临时存放点
		for (int i = 0; i < arr.length-1; i++) {
			k=i;
            //从剩余的未排序元素中寻找到最小元素存放到临时存放点
			for (int j = i; j < arr.length; j++) {
				if(arr[j]<arr[k]) {
					k=j;
				}
			}
			tmp=arr[i];
			arr[i]=arr[k];
			arr[k]=tmp;
		}
	}

3.插入排序

每步将一个待排序的记录，按其关键码值的大小插入前面已经排序的文件中适当位置上，直到全部插入完为止。插入排序法,算法适用于少量数据的排序，时间复杂度O(n^2)。是稳定的排序方法。

下面这个动图来自郭耀华's Blog（不会做动图，这动图做的太好了）

	/**
	 * 插入排序
	 * @param arr
	 */
	public static void sort(long array[]) {
		int j;
	        //从下标为1的元素开始选择合适的位置插入，因为下标为0的只有一个元素，默认是有序的
	        for(int i = 1 ; i < array.length ; i++){
	            long tmp = array[i];//记录要插入的数据
	            j = i;
	            while(j > 0 && tmp < array[j-1]){//从已经排序的序列最右边的开始比较，找到比其小的数
	                array[j] = array[j-1];//向后挪动
	                j--;
	            }
	            array[j] = tmp;//存在比其小的数，插入
	        }
	}

三. 栈和队列

我们是用数组实现的，在定义数组类型的时候，也就规定了存储在栈或队列中的数据类型，如果想存储不同类型的数据声明为Object（在下一节链表中用Object实现）

3.1栈

栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

栈作为一种数据结构，是一种只能在一端进行插入和删除操作的特殊线性表。它按照先进后出（LIFO, Last In First Out）的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据（最后一个数据被第一个读出来）。栈具有记忆作用，对栈的插入与删除操作中，不需要改变栈底指针。

java 模拟栈实现

public class MyStack {
	//底层实现是数组
	private long [] arr;
	private int top;
	
	public MyStack() {
		arr=new long[10];
		top=-1;
	}
	
	public MyStack(int maxsize) {
		arr=new long[maxsize];
		top=-1;
	}
	
	/**
	 * 添加数据
	 */
	public void push(int value) {
		arr[++top]= value;
	}
	/**
	 * 移除数据
	 */
	public long pop() {
		return arr[top--];
	}
	
	/**
	 * 查看数据
	 */
	public long peek() {
		return arr[top];
	}
	
	/**
	 * 判断是否为空
	 */
	public boolean isEmpty() {
		return top == -1;
	}
	/**
	 * 判断是否满了
	 */
	public  boolean isFull() {
		return top == arr.length-1;
	}
}

3.2 队列

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。队列中没有元素时，称为空队列。

队列的数据元素又称为队列元素。在队列中插入一个队列元素称为入队，从队列中删除一个队列元素称为出队。因为队列只允许在一端插入，在另一端删除，所以只有最早进入队列的元素才能最先从队列中删除，故队列又称为先进先出（FIFO—first in first out）线性表。

java模拟单向队列

public class MyQueue {
	//底层使用数组
	private long arr[];
	//有效数据
	private int elements;
	//队头
	private int front;
	//队尾
	private int end;
	public MyQueue() {
		arr =new long [10];
		elements=0;
		front=0;
		end=-1;
	}
	public MyQueue(int maxsize) {
		arr =new long [maxsize];
		elements=0;
		front=0;
		end=-1;
	}
	
	/**
	 * 添加数据，队尾插入
	 */
	public void insert(long value) {
		
		arr[++end]=value;
		elements++;
	}
	/**
	 * 删除数据
	 */
	public long remove() {
		elements--;
		return arr[front--];
	}
	/**
	 * 查看数据，从队头查看
	 */
	public long peek() {
		return arr[front];
	}
	/**
	 * 判断是否为空
	 */
	public boolean isEmpty() {
		return elements==0;
	}
	public boolean isFull() {
		return elements ==arr.length;
	}
}

单项队列如果满了，在进行插入会报错，数组溢出。所以改为循环队列。

java模拟循环队列

修改上述添加和删除方法即可

	/**
	 * 添加数据，队尾插入
	 */
	public void insert(long value) {
		if(end==arr.length -1) {//如果数据满了。就从头开始
			end=-1;
		}
		
		arr[++end]=value;
		elements++;
	}
	/**
	 * 删除数据
	 */
	public long remove() {
		long value =arr[front++];
        /*ps：这里是假清除，此处只是将要删除的数据返回将有效数据但未清除
        若想真正清除可以将long数组改为Object然后用如下方式
        Object value=null;
        value =arr[front];
        arr[front] = null;
        front++
        */
		if(front == arr.length) {//如果队头到末尾，从头开始
			front=0;
		}
		elements--;
		return value;
	}

四. 链表

链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构，操作复杂。由于不必须按顺序存储，链表在插入的时候可以达到O(1)的复杂度，比另一种线性表顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要O(n)的时间，而线性表和顺序表相应的时间复杂度分别是O(logn)和O(1)。

4.1单向链表

单链表是链表中结构最简单的。一个单链表的节点(Node)分为两个部分，第一个部分(data)保存或者显示关于节点的信息，另一个部分存储下一个节点的地址。最后一个节点存储地址的部分指向空值。

java实现单向链表

/**
 * 节点
 * @author Loserfromlazy
 *
 */
public class Node {
	//数据域
	public Object data;
	//节点域
	public Node next;
	
	public Node(Object value) {
		this.data=value;
	}
	
	/**
	 * 显示
	 */
	public void display() {
		System.out.print(data+" ");
	}
}
/**
 * @author Loserfromlazy
 * 链表
 */
public class LinkList {
	//头节点
	private Node first;
	//节点的个数
	private int size;
	public LinkList() {
		first=null;
	}
	
	/**
	 * 插入一个节点，在头节点进行插入
	 */
	public void insertFirst(Object value) {
		Node node = new Node(value);//待插入的节点
		if(size==0) {
			first= node;
		}else {
			node.next=first;//将新插入的节点的下一个节点指向头节点
			first=node;//将新插入的节点变成头节点，这样就可以实现在头节点之前插入节点
		}
		size++;
	}
	
	/**
	 * 删除一个节点，在头节点进行删除
	 */
	public Node deleteFirst() {
		Node node= first;
		first=node.next;//将头节点的下一个节点变成头节点，这样就可以删除当前头节点
		size--;
		return node;
	}
	
	public void display() {
		Node current =first;
		while(current!=null) {
			current.display();
			current=current.next;
		}
		System.out.println();
	}
	
	/**
	 * 查找结点
	 */
	public Node find(Object value) {
		Node current =first;
		int tempSize=size;
		while(tempSize>0) {
			if(value.equals(current.data)){
				return current;
			}else {
				current=current.next;
			}
			tempSize--;
		}
		
		return null;
	}
	
	/**
	 * 删除节点，根据数据域进行删除
	 */
	public boolean delete(Object value) {
		if(size==0) {
			return false;
		}
		Node current =first;
		Node previous =first;
		while(current.data!=value) {//当查到相等的数据current就是要找的节点
			if(current.data==null) {
				return false;
			}else {
                //指向下一个节点继续查
				previous=current;
				current =current.next;
			}
		}
		if(current==first) {
			first=current.next;
			size--;
		}else {
            //将前一个节点直接指向下一个节点，即跳过current节点，就可以完成删除
			previous.next=current.next;
			size--;
		}
		return true;
	}
}

4.2 双端列表

链表中保存着对最后一个链节点的引用。

对于单项链表，如果想在尾部添加一个节点，那么必须从头部一直遍历到尾部，找到尾节点，然后在尾节点后面插入一个节点。如果多个对尾节点的引用，那么会简单很多。

java实现双端列表

主要不同就是新增了一个尾节点，所以修改insertFirst和deleteFirst方法，新增insertLast方法

/**
 * @author Loserfromlazy
 * 双端链表
 */
public class FirstLastLinkList {
	//头节点
	private Node first;
	//尾节点
	private Node last;
	//节点的个数
	private int size;
	public FirstLastLinkList() {
		first=null;
	}
	
	/**
	 * 插入一个节点，在头节点进行插入
	 */
	public void insertFirst(Object value) {
		Node node = new Node(value);
		if(size==0) {
			first=node;
			last= node;//修改的地方
		}else {
			node.next=first;
			first=node;
		}
		size++;
	}
	/**新增的方法
	 * 插入一个节点，从尾节点进行插入
	 */
	public void insertLast(Object value) {
		Node node = new Node(value);
		if(size==0) {
			first=node;
			last=node;
		}else {
            //将待加入的节点插入到尾节点之后，将新插入的节点变成尾节点
			last.next=node;
			last=node;
		}
		size++;
	}
	/**
	 * 删除一个节点，在头节点进行删除
	 */
	public Node deleteFirst() {
		Node node= first;
		if(first.next==null) {//修改的地方，如果头节点没有下一个节点，那么尾节点也为空
			last=null;
		}else {
			first=node.next;
		}
		
		size--;
		return node;
	}
	
	public void display() {
		Node current =first;
		while(current!=null) {
			current.display();
			current=current.next;
		}
		System.out.println();
	}

4.3 双向链表

我们知道单向链表只能从一个方向遍历，那么双向链表它可以从两个方向遍历。

PS：注意双端链表与双向链表的区别：双端链表只是增加了一个指向尾节点的节点，但这个节点没有向回指的指针。索引不能进行双向遍历。而双向链表在每一个节点都增加了向回指的指针所以可以双向遍历。

java双向链表的实现

package ch4;

/**
 * 节点
 * @author Loserfromlazy
 *
 */
public class DoubleNode {
	//数据域
	public Object data;
	//节点域
	public DoubleNode next;
	//向前的指针
	public DoubleNode previous;
	
	public DoubleNode(Object value) {
		this.data=value;
	}
	
	/**
	 * 显示
	 */
	public void display() {
		System.out.print(data+" ");
	}
}
/**
 * @author Loserfromlazy
 * 双端链表
 */
public class DoubleLinkList {
	//头节点
	private DoubleNode first;
	//尾节点
	private DoubleNode last;
	//节点的个数
	private int size;
	public DoubleLinkList() {
		first=null;
		size=0;
		last=null;
	}
	
	/**
	 * 插入一个节点，在头节点进行插入
	 */
	public void insertFirst(Object value) {
		DoubleNode node = new DoubleNode(value);
		if(size==0) {
			first=node;
			last= node;
            size++;
		}else {
            //将头节点的前一个节点变成新插入的节点，然后将新插入的节点的下一个节点指向头节点，这样就可以实现将头节点与新插入的节点相连，然后将新插入的节点变为头节点即可
			first.previous=node;
            node.next=first;
			first=node;
            size++;
		}
		
	
	}
	/**
	 * 插入一个节点，从尾节点进行插入
	 */
	public void insertLast(Object value) {
		DoubleNode node = new DoubleNode(value);
		if(size==0) {
			first=node;
			last=node;
		}else {
			last.next=node;
			node.previous=last;//将尾节点与新插入的节点相连
			last=node;
		}
		size++;
	}
	/**
	 * 删除一个节点，在头节点进行删除
	 */
	public DoubleNode deleteFirst() {
		DoubleNode node= first;
		if(first.next==null) {
			last=null;
		}else {
            //将头节点的下一个节点的前节点变为空这样就切断了两个节点的联系
			first.next.previous=null;
		}
		first=node.next;
		size--;
		return node;
	}
	/**
	 * 删除节点，从尾部进行删除
	 */
	public DoubleNode deleteLast() {
		DoubleNode node= last;
		if(first.next==null) {
			first=null;
		}else {
            //将尾节点的前一个节点的下一个节点变为空这样就切断了两个节点的联系
			last.previous.next=null;
			
		}
		last=last.previous;
		size--;
		return node;
	}
	public void display() {
		DoubleNode current =first;
		while(current!=null) {
			current.display();
			current=current.next;
		}
		System.out.println();
	}
	
	/**
	 * 查找结点
	 */
	public DoubleNode find(Object value) {
		DoubleNode current =first;
		int tempSize=size;
		while(tempSize>0) {
			if(value.equals(current.data)){
				return current;
			}else {
				current=current.next;
			}
			tempSize--;
		}
		
		return null;
	}
	
	/**
	 * 删除节点，根据数据域进行删除
	 */
	public boolean delete(Object value) {
		if(size==0) {
			return false;
		}
		DoubleNode current =first;
		DoubleNode previous =first;
		while(current.data!=value) {
			if(current.data==null) {
				return false;
			}else {
				current =current.next;
			}
		}
		if(current==first) {
			first=current.next;
			size--;
		}else {
			current.previous.next=current.next;//切断联系
			size--;
		}
		return true;
	}
	public boolean isEmpty() {
		if(size==0) {return true;}
		return false;
	}
}

五. 递归 Recursive

5.1 定义

编程语言中，函数Func(Type a,……)直接或间接调用函数本身，则该函数称为递归函数

递归必须满足三个条件：

1. 在每一次调用自己时，必须是（在某种意义上）更接近于解；
2. 必须有一个终止处理或计算的准则。

当边界条件不满足，递归前进，不满足递归返回；

5.2 三角数字

在该数列中第n项由第n-1项加第n项得到:

三角数即正整数前n项和： 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78,..n(n+1)/2

比如：1，1+2=3，1+2+3=6........

java实现三角数字

public static int getNumber(int n){//n为第几项
	int total =0;
    while(n>0){
        total=total+n;
        n--;
    }
    return total;
}

java递归实现三角数字

public static int getNumberByRecursive(int n){//n为第几项
    if(n==1){
        return 1;
    }else{
        return n+getNumberByRecursive(n-1);
    }
}

5.3 Fibonacci数列

斐波那契数列（Fibonacci sequence），又称黄金分割数列、因列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……

java递归方法实现

此方法的空间复杂度O(2^n）越来越高，最终达到最大深度导致栈溢出。一般不用此方法实现斐波那契数列。

/**
* 递归方法实现
* f(n) = f(n - 1) + f(n - 2)
* 最高支持 n = 92 ，否则超出 Long.MAX_VALUE
* @param num n 
* @return f(n) 
*/
public static long Fibonacci(int n) {
    if(n < 1)
        return 0;
    if(n < 3)
        return 1;
    return fibRec(n - 1) + fibRec(n - 2);
}

对上述方法改良：用平推方法实现（此方法不做深究，我这里主要是举递归的例子）

public static long fibLoop(int num) {
    if(num < 1 || num > 92)
        return 0;
    long a = 1;
    long b = 1;
    long temp;
    for(int i = 3; i <= num; i++) {
        temp = a;
        a = b;
        b += temp;
    }
    return b;
}

5.4 汉诺塔

汉诺塔：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

使用递归思想解决汉诺塔

如果有三个盘子，只要将最上面的两个盘子解决。如果有四个盘子，只要将最上面的三个盘子解决。依次类推无论有多少个盘子，我们都将其看做只有两个盘子。简单来说，递归算法：

1. 从初始塔座A上移动包含n-1个盘子到中介塔座B上。
2. 将初始塔座A上剩余的一个盘子（最大的一个盘子）放到目标塔座C上。
3. 将中介塔座B上n-1个盘子移动到目标塔座C上。

java实现汉诺塔

	/**
	 * 移动盘子
	 * @param topN 移动的盘子数
	 * @param from 起始塔座
	 * @param inter 辅助塔座
	 * @param to	目标塔座
	 */
	public static void doTower(int topN,String from,String inter,String to) {
		if(topN==1) {
			System.out.println("盘子"+topN+"从"+from+"塔座到"+to+"塔座");
		}else {
			doTower(topN-1,from,to,inter);
			System.out.println("盘子"+topN+"从"+from+"塔座到"+to+"塔座");
			doTower(topN-1, inter, from, to);
		}
	}

5.5 整数划分

此问题是求正整数n表示成一系列正整数的和

将最大加数n不大于m的的划分记作q(n,m),比如q(6,4)就是把6用小于等于4的数进行划分

6

5+1

4+2，4+1+1

3+3，3+2+1，3+1+1

2+2+2，2+2+1+1，2+1+1+1+1

1+1+1+1+1+1

具体递归如下图

当m=1，n=1明显就是1；

当n<m时，显然是不对的，所以这种情况等于q（n,n）

当n=m时就是q(n,n)，这需要继续递归所以q(n,m)=q(n,m-1),如果不理解看上面q(6,6)=q(6,5)+1

当n>m时，q(n,m)=q(n,m-1)+q(n-m,n-m)，如果不理解看上面q(6,4)有四行，可以将其分为两部分q(6,3)和q(2,4)包括（4+2,4+1+1;）q(2,4)可以写成q(2,2)

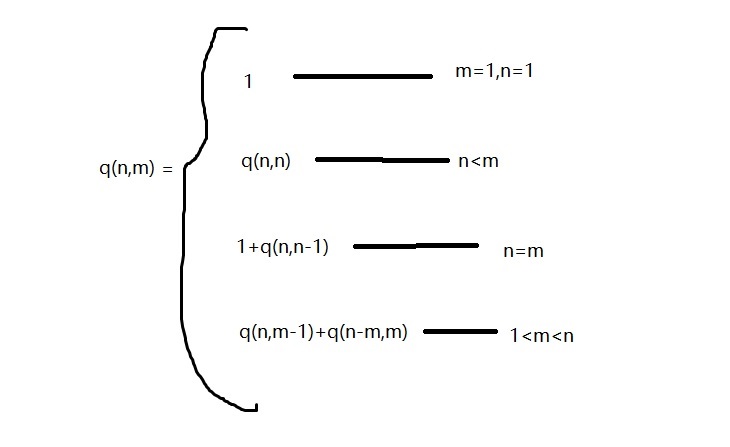
java代码

public class Huafen {
    public static void main(String[] args) {
        System.out.println(split(6));
    }
    public static int split(int n) {
        return p(n,n);
    }
    public static int p(int n,int m) {
        if(n==1 || m==1) {
            return 1;
        } else if(n<m) {
            return p(n,n);
        } else if(n==m) {
            return p(n,n-1)+1;
        } else if(n>m) {
            return  p(n,m-1) + p(n-m,m);
        }
        return -1;
    }
}
结果为11

5.6 棋盘覆盖

解决思路：应用分治法

分治的技巧在于如何划分棋盘，使划分后的子棋盘的大小相同，并且每个子棋盘均包含一个特殊方格，从而将原问题分解为规模较小的棋盘覆盖问题。k>0 时，可将2^k×2k的棋盘划分为4个2^（k-1）×2（k-1）的子棋盘。这样划分后，由于原棋盘只有一个特殊方格，所 以，这4个子棋盘中只有一个子棋盘包含该特殊方格，其余3个子棋盘中没有特殊方格。为了将这3个没有特殊方格的子棋盘转化为特殊棋盘，以便采用递归方法求 解，可以用一个L型骨牌覆盖这3个较小棋盘的会合处，从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种划分策略， 直至将棋盘分割为1×1的子棋盘。

java核心代码：

/**
 * 棋盘覆盖问题
 * @author  Loserfromlazy
 */
public class ChessBoard {
    private static int[][] board ;
    int tile=0;//表示L型骨牌的编号

    /**
     * 棋盘覆盖函数
     * @param tr 棋盘左上角行号
     * @param tc 棋盘左上角列号
     * @param dr 特殊棋子的行
     * @param dc 特殊棋子列
     * @param size 棋盘大小
     */
    public void chessBoard(int tr,int tc,int dr,int dc,int size){
        if (size==1) return;
        int t=++tile;
        int s = size/2;//每一次将大棋盘化为一半的子棋盘
        //处理左上角棋盘
        if(dr < tr + s && dc< tc + s)//左上角子棋盘有特殊棋子
            chessBoard(tr,tc,dr,dc,s);//递归处理
        else//处理无特殊棋子的左上角子棋盘
        {
            board[tr+s-1][tc+s-1] = t;//设左上角子棋盘的右下角为特殊棋子，用t型的骨牌覆盖。
            chessBoard(tr,tc,tr+s-1,tc+s-1, s);//递归处理
        }
        //处理右上角棋盘
        if(dr < tr+s && dc >=tc+s)//右上角棋盘有特殊棋子
        {
            chessBoard(tr,tc+s,dr,dc,s);//递归处理
        }
        else
        {
            board[tr+s-1][tc+s] =t;//设右上角子棋盘的左下角为特殊棋子，用t型的骨牌覆盖。
            chessBoard(tr,tc+s,tr+s-1,tc+s,s);//递归处理
        }
        //处理左下角棋盘
        if(dr >=tr+s && dc<tc+s)//左下角子棋盘有特殊棋子
        {
            chessBoard(tr+s,tc,dr,dc,s);//递归处理
        }
        else
        {
            board[tr+s][tc+s-1] = t;//设左下角子棋盘的右上角为特殊棋子，用t型的骨牌覆盖。
            chessBoard(tr+s,tc,tr+s,tc+s-1,s);//递归处理
        }
        //处理右下角棋盘
        if(dr>=tr+s&& dc>= tc+s)//右下角棋盘有特殊棋子
        {
            chessBoard(tr+s,tc+s,dr,dc,s);//递归处理
        }
        else
        {
            board[tr+s][tc+s] = t;//设子棋盘右下角的左上角为特殊棋子，用t型的骨牌覆盖。
            chessBoard(tr+s,tc+s,tr+s,tc+s,s);//递归处理
        }
    }

    public static void main(String[] args) {
        详见我的github
    }
}

六. 希尔排序和快速排序

希尔排序

希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。（直接插入排序见上面）

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

缺陷：假如一个很小的的数据在靠有的排序上，那么要将该数据排序到正确的位置上，则，所有的中间数据都需要向右移动一位。

优点：希尔排序通过加大插入排序中元素之间的间隔，并对这些间隔的元素进行插入排序，从而使得数据可以大幅度的移动。当完成该间隔的排序后，希尔排序会减少数据的间隔在进行排序。依次进行下去。

希尔排序间隔的计算

希尔的原稿中，他建议间隔选为N/2。但是间隔的初始值为1，通过计算最大间隔，直到该间隔大于数组的大小时停止，最大间隔为不大于数组大小的最大值，这是最好的间隔序列。

最好的间隔序列h=h*3+1。即1，4，13，40...序列。间隔的减少：h=(h-1)/3来计算

java实现希尔排序

public class ShellSort {
	public static void sort(long[] arr) {
		// 初始化间隔
		int h = 1;
		// 计算最大间隔
		while (h < arr.length / 3) {
			h = h * 3 + 1;
		}
		while (h > 0) {
			// 进行插入排序
			for (int i = h; i < arr.length; i++) {// 从最大间隔开始进行排序
				long temp = arr[i];
				int j = i;
				while (j > h - 1 && temp <= arr[j - h]) {
                    // 如果比同间隔小则交换两个数，比如a[4]<a[1];a[5]<a[2];a[6]<a[3]....
                    //此处如果是插入排序则是插入到排好的序列中
					arr[j] = arr[j - h];
					j -= h;
				}
				arr[j] = temp;
			}
			h = (h - 1) / 3;// 减小间隔，继续排序
		}
	}
}

快速排序

基于分治的思想，是冒泡排序的改进型。快速排序通过将一个数组划分为两个子数组，然后通过调用自身为每一个子数组进行快速排序。

如何进行划分：主要是设定关键字，将比关键字小的数据放在一组，比关键字大的数据放在一组。

下面这个动图来自郭耀华's Blog（不会做动图，这动图做的太好了）

/**
 * 快速排序
 */
public class QuickSort {
    /**
     * 划分数组
     * @param arr
     * @param left  起点位置
     * @param right 终点位置
     *
     */
    public static int partition(long arr[],int left,int right){
        int leftPtr = left;//关键字为arr[left],所以下面++leftPtr，及跳过关键字
        int rightPtr=right+1;//下面为--rightPtr，所以此处加1
        long point =arr[left];
        while(true){
            //循环，将比关键字小的留在左边
            while (leftPtr < right && arr[++leftPtr] < point);
            //循环，将比关键字大的留在右边
            while (rightPtr > 0 && arr[--rightPtr] > point);
            if (leftPtr>=rightPtr){//左右游标相遇时停止
                break;
            }else{//为相遇时交换元素
                swap(arr,leftPtr,rightPtr);
            }
        }
        //最后交换左右游标相遇时的所指的元素与关键字交换
        swap(arr,left,rightPtr);
        return rightPtr;//返回关键字位置
    }
    public static void sort(long arr[],int left,int right){
        //设置跳出条件
        if(left>=right){
            return;
        }else {

            int part=partition(arr,left,right);
            sort(arr,left,part-1);//对上一轮排序，关键字左边的子数组递归
            sort(arr,part+1,right);//对上一轮排序，关键字右边的子数组递归 ;
        }
    }
    /**
     * 显示数组
     * @param arr
     */
    public static void display(long [] arr){
        for (long x : arr) {
            System.out.print(x+"  ");
        }
        System.out.println();
    }
    /**
     * 交换
     * @param arr
     * @param i
     * @param j
     */
    public static void swap(long [] arr,int i,int j){
        long tmp=arr[i];
        arr[i]=arr[j];
        arr[j]=tmp;
    }
}

七. 二叉树

7.1树

树是由根结点和若干颗子树构成的。树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的结点，所定义的关系称为父子关系。父子关系在树的结点之间建立了一个层次结构。在这种层次结构中有一个结点具有特殊的地位，这个结点称为该树的根结点，或称为树根。

为什么需要树？

有序数组插入或删除数据慢；链表查找数据太慢

树中能快速插入删除及查找数据

空集合也是树，称为空树。空树中没有结点。

结点的度：一个结点含有的子结点的个数称为该结点的度；

叶结点或终端结点：度为0的结点称为叶结点；

非终端结点或分支结点：度不为0的结点；

双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点；

孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点；

兄弟结点：具有相同父结点的结点互称为兄弟结点；

树的度：一棵树中，最大的结点的度称为树的度；

结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推；

树的高度或深度：树中结点的最大层次；

堂兄弟结点：双亲在同一层的结点互为堂兄弟；

结点的祖先：从根到该结点所经分支上的所有结点；

子孙：以某结点为根的子树中任一结点都称为该结点的子孙。

森林：由m（m>=0）棵互不相交的树的集合称为森林；

7.2 二叉树

树的每个节点最多只能有两个子节点

二叉树是递归定义的，其结点有左右子树之分，逻辑上二叉树有五种基本形态：

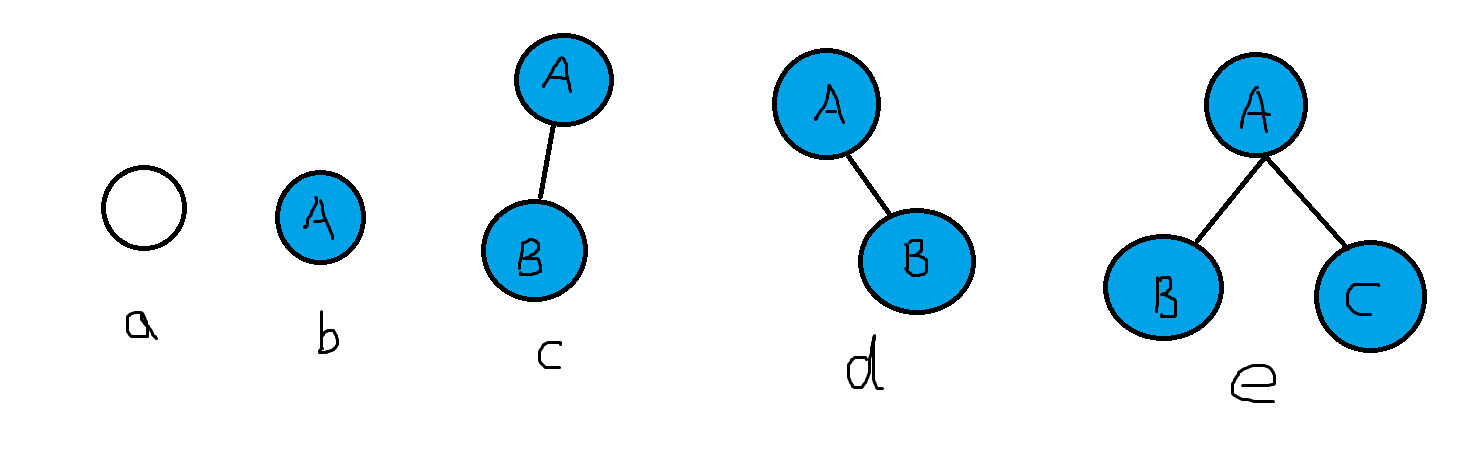
(1)空二叉树——如图(a)；

(2)只有一个根结点的二叉树——如图(b)；

(3)只有左子树——如图(c)；

(4)只有右子树——如图(d)；

(5)完全二叉树——如图(e)。

注意：尽管二叉树与树有许多相似之处，但二叉树不是树的特殊情形。

7.3 二叉排序树

二叉排序树（Binary Sort Tree），又称二叉查找树Binary Search Tree），亦称二叉搜索树。是数据结构中的一类。在一般情况下，查询效率比链表结构要高。

二叉排序树是一棵空树，或者是具有下列性质的二叉树

（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；

（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

（3）左、右子树也分别为二叉排序树；

（4）没有键值相等的结点。

/**
 * 二叉树节点
 */
public class Node {
    //数据项,设置为default可以同一个包访问，方便tree访问
    long data;
    //左子节点
    Node leftChild;
    //右子节点
    Node rightChild;

    public Node(long data){
        this.data=data;
    }
    //输出数据项
    public void display(){
        System.out.println(data);
    }
}
这里是两个文件
/**
 * 二叉树类
 */
public class Tree {
    //根节点，测试Tree类时可以改为public，查看数据
    private Node root;
    /**
     * 插入节点
     * @param value
     */
    public void insert(long value){
    }
    /**
     * 查找节点
     * @param value
     */
    public void find(long value){
    }
    /**
     * 删除节点
     * @param value
     */
    public void delete(long value){
    }
    //。。。。
}

7.4 二叉树的插入和查找

插入节点

从根节点开始查找一个相应的节点，这个节点将成为新插入既然点的父节点，当父节点找到后，通过判断新节点的值比父节点的值的大小来决定链接到左子节点还是右子节点。

java代码如下，可直接放到上面插入节点代码处

/**
 * 插入节点
 * @param value
 */
public void insert(long value){
    //封装节点
    Node newNode = new Node(value);
    //引用当前节点
    Node current =root;
    //引用父节点
    Node parent;
    //如果root为null，第一次插入时
    if (root == null){
        root = newNode;
    }else {
        while (true) {
            //父节点指向当前节点
            parent = current;
            //如果当前节点数据比插入的大，则向左走
            if (current.data > value) {
                current = current.leftChild;
                if (current == null){//如果左子节点为空
                    parent.leftChild = newNode;//插入新值，返回
                    return;
                }
            } else {
                current = current.rightChild;
                if (current == null){//如果右子节点为空
                    parent.rightChild = newNode;//插入新值，返回
                    return;
                }
            }
        }
    }
}

查找结点

从根节点开始查找，如果查找的节点值比当前节点小，则继续查左子树，否则查找右子树。

Java代码如下：

/**
 * 查找节点
 * @param value
 */
public Node find(long value){
    //引用当前节点，从根节点开始
    Node current = root;
    //循环，查找值不等于当前节点的数据项
    while (current.data != value){
        //比较当前节点大小与查找值
        if (current.data > value){
            current = current.leftChild;
        }else if(current.data < value) {
            current =current.rightChild;
        }else {
            return null;
        }
    }
    return current;
}

7.5 遍历树

遍历树是根据一种特定的顺序访问树的每一个节点。比较常用的有前序遍历，中序遍历和后序遍历。而二叉搜索树最常用的是中序遍历。

前序遍历:（根左右）访问根节点——>前序遍历左子树——>前序遍历右子树

中序遍历（左根右）:中序遍历左子树——>访问根节点——>中序遍历右子树

后序遍历（左右根）:后序遍历左子树——>后序遍历右子树——>访问根节点

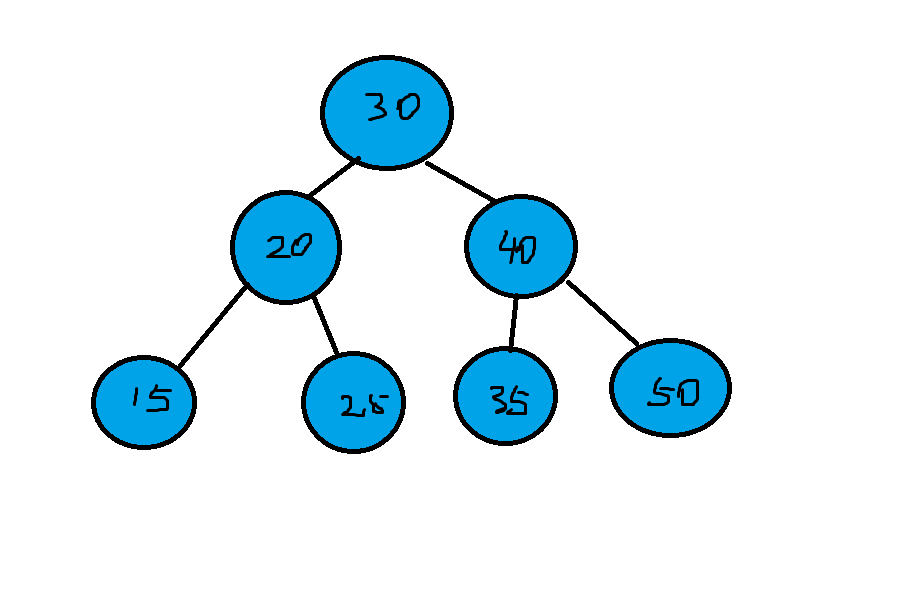
前序遍历：30-20-15-20-40-35-50

中序遍历：15-20-25-30-35-40-50

后序遍历：15-25-20-35-50-40-30

java代码如下：

package ch7;

/**
 * 二叉树类
 */
public class Tree {
    //根节点
    public Node root;

    /**
     * 插入节点
     * @param value
     */
    public void insert(long value){
        //封装节点
        Node newNode = new Node(value);
        //引用当前节点
        Node current =root;
        //引用父节点
        Node parent;
        //如果root为null，第一次插入时
        if (root == null){
            root = newNode;
        }else {
            while (true) {
                //父节点指向当前节点
                parent = current;
                //如果当前节点数据比插入的大，则向左走
                if (current.data > value) {
                    current = current.leftChild;
                    if (current == null){//如果左子节点为空
                        parent.leftChild = newNode;//插入新值，返回
                        return;
                    }
                } else {
                    current = current.rightChild;
                    if (current == null){//如果右子节点为空
                        parent.rightChild = newNode;//插入新值，返回
                        return;
                    }
                }
            }
        }
    }

    /**
     * 查找节点
     * @param value
     */
    public Node find(long value){
        //引用当前节点，从根节点开始
        Node current = root;
        //循环，查找值不等于当前节点的数据项
        while (current.data != value){
            //比较当前节点大小与查找值
            if (current.data > value){
                current = current.leftChild;
            }else if(current.data < value) {
                current =current.rightChild;
            }else {
                return null;
            }
        }
        return current;
    }

    /**
     * 前序遍历
     * @param localNode
     */
    public void frontOrder(Node localNode){
        if (localNode != null){
            //访问根节点
            System.out.println(localNode.data+" ");
            //前序遍历左子树
            frontOrder(localNode.leftChild);
            //前序遍历右子树
            frontOrder(localNode.rightChild);
        }
    }

    /**
     * 中序遍历
     * @param localNode
     */
    public void inOrder(Node localNode){
        if (localNode != null){
            //中序遍历左子树
            inOrder(localNode.leftChild);
            //访问根节点
            System.out.println(localNode.data+" ");
            //中序遍历右子树
            inOrder(localNode.rightChild);
        }
    }
    /**
     * 后序遍历
     * @param localNode
     */
    public void afterOrder(Node localNode){
        if (localNode != null){
            //后序遍历左子树
            afterOrder(localNode.leftChild);
            //后序遍历右子树
            afterOrder(localNode.rightChild);
            //访问根节点
            System.out.println(localNode.data+" ");
        }
    }

    /**
     * 查找中序后继节点
     * @param delNode
     * @return
     */
    public Node getSuccessor(Node delNode){
        Node successor =delNode;
        Node successorParent = delNode;
        Node current =delNode.rightChild;

        while (current != null){
            successorParent = successor;//保存父节点的引用
            successor =current;//保存当前节点的引用
            current = current.leftChild;
        }
        //将中序后继节点与删除节点替换
        if (successor != delNode.rightChild){
            successorParent.leftChild = successor.rightChild;//如果这个中序后继节点还有右子节点，将他变成这个中序后继节点位置
            successor.rightChild = delNode.rightChild;
        }
        return successor;
    }
    /**
     * 删除节点
     * @param value
     */
    public boolean delete(long value){
        //引用当前节点
        Node current =root;
        //引用当前节点父节点
        Node parent = root;
        //判断是否是左子节点
        boolean isLeftChild = false;
        //查找节点
        while (current.data!= value){
            parent=current;
            if (current.data > value){
                current = current.leftChild;
                isLeftChild = true;
            }else if(current.data < value) {
                current =current.rightChild;
                isLeftChild = false;
            }else {
                return false;
            }
        }

        //删除节点
        if (current.leftChild == null && current.rightChild ==null){//删除叶子节点，该节点没有子节点
            if (current == root){
                root = null;
            }
            //如果是父节点的左子节点
            else if (isLeftChild){
                parent.leftChild=null;
            }else {
                parent.rightChild=null;
            }
            return true;
        }else if (current.rightChild == null){//如果节点只有一个左节点
            if (current == root){//跳过待删除节点，让待删除节点的左子节点变成根节点
                root=current.leftChild;
            }
            else if (isLeftChild){//如果待删除节点是左子节点，让父节点的左子节点等于待删除节点的左子节点
                parent.leftChild=current.leftChild;
            }else {//如果待删除节点是右子节点，让父节点的右子节点等于待删除节点的左子节点
                parent.rightChild=current.leftChild;
            }
            return true;
        }else if (current.leftChild == null){//如果节点只有一个右节点
            if (current == root){//跳过待删除节点，让待删除节点的右子节点变成根节点
                root=current.rightChild;
            }else if (isLeftChild){//如果待删除节点是左子节点，让父节点的左子节点等于待删除节点的右子节点
                parent.leftChild =current.rightChild;
            }else {
                parent.rightChild=current.rightChild;
            }
            return true;
        }else {//如果有两个子节点
            Node successor =getSuccessor(current);
            if (current == root){
                root =successor;
            }else if (isLeftChild){
                parent.leftChild=successor;
            }else {
                parent.rightChild=successor;
            }
            successor.leftChild=current.leftChild;

        }
        return false;
    }
}

7.6 删除节点

删除节点非常复杂，在删除钱首先要查找要删除的节点，找到节点后还有三种情况：

1. 该节点是叶子节点，没有子节点

   要删除叶子节点，只需要改变该节点的父节点的引用值为null即可。

   

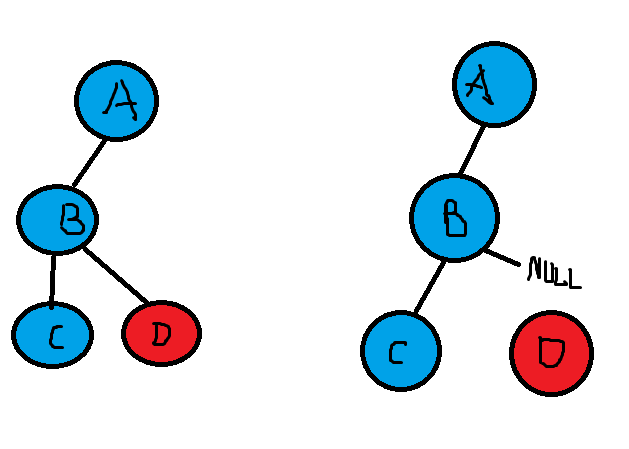
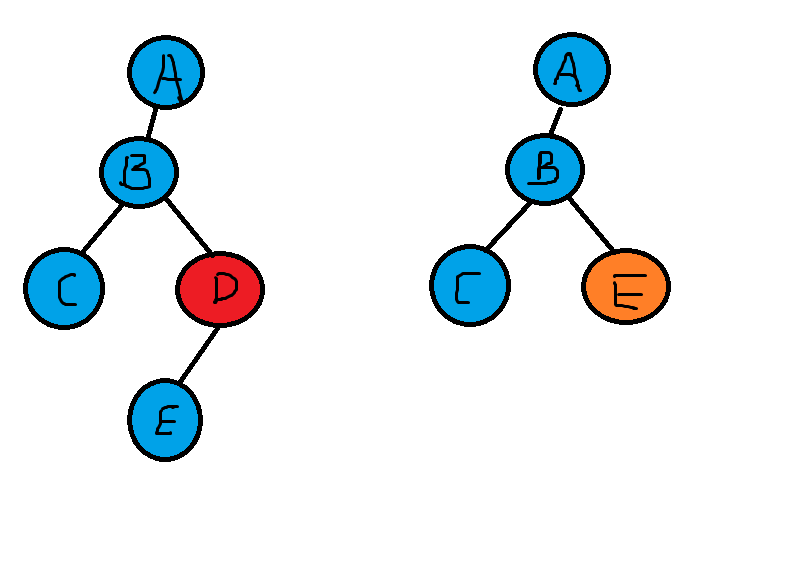
2. 该节点有一个子节点

   改变父节点的引用，将其直接指向要删除节点的子节点

   

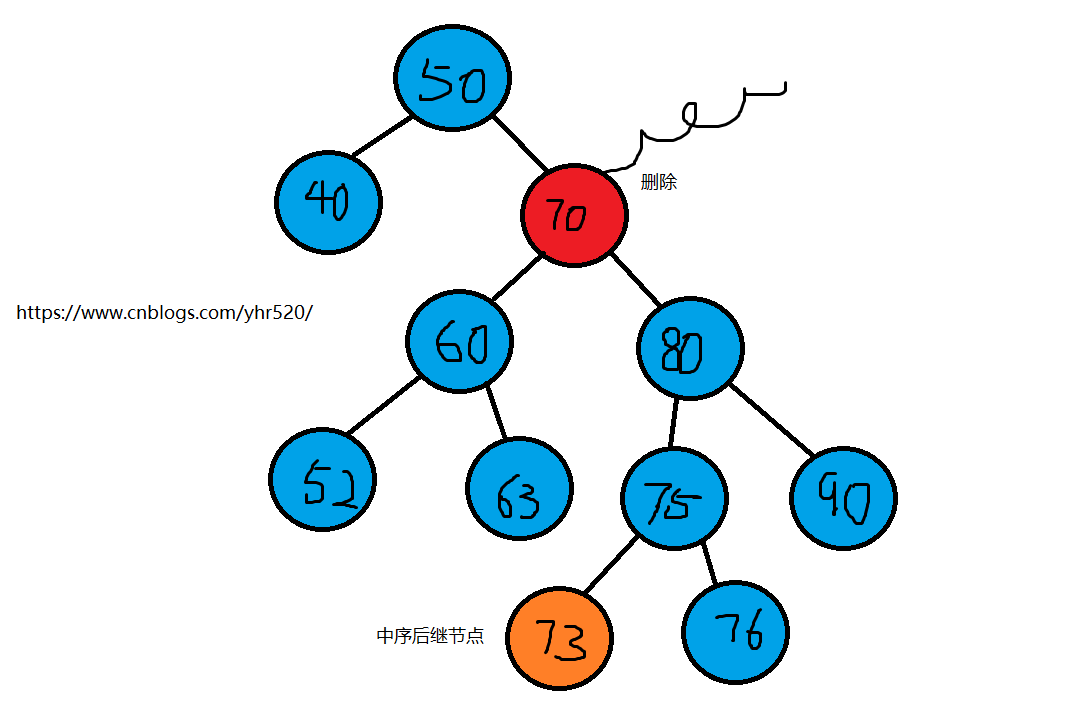
3. 该节点有两个字节点

   需要使用它的中序后继来代替该节点。实际上就是要找比删除节点关键值大的节点集合中最小的一个节点，只有这样代替删除节点后才能满足二叉搜索树的特性。

   程序找到删除节点的右节点，然后转到该右节点的左子节点，依次顺着左子节点找下去，最后一个左子节点即是后继节点；如果该右节点没有左子节点，那么该右节点便是后继节点。

   后继节点也就是：比删除节点大的最小节点。

   

java代码：

package ch7;
/**
 * 二叉树类
 */
public class Tree {
    //根节点
    public Node root;

    /**
     * 插入节点
     * @param value
     */
    public void insert(long value){
        //封装节点
        Node newNode = new Node(value);
        //引用当前节点
        Node current =root;
        //引用父节点
        Node parent;
        //如果root为null，第一次插入时
        if (root == null){
            root = newNode;
        }else {
            while (true) {
                //父节点指向当前节点
                parent = current;
                //如果当前节点数据比插入的大，则向左走
                if (current.data > value) {
                    current = current.leftChild;
                    if (current == null){//如果左子节点为空
                        parent.leftChild = newNode;//插入新值，返回
                        return;
                    }
                } else {
                    current = current.rightChild;
                    if (current == null){//如果右子节点为空
                        parent.rightChild = newNode;//插入新值，返回
                        return;
                    }
                }
            }
        }
    }

    /**
     * 查找节点
     * @param value
     */
    public Node find(long value){
        //引用当前节点，从根节点开始
        Node current = root;
        //循环，查找值不等于当前节点的数据项
        while (current.data != value){
            //比较当前节点大小与查找值
            if (current.data > value){
                current = current.leftChild;
            }else if(current.data < value) {
                current =current.rightChild;
            }else {
                return null;
            }
        }
        return current;
    }

    /**
     * 前序遍历
     * @param localNode
     */
    public void frontOrder(Node localNode){
        if (localNode != null){
            //访问根节点
            System.out.println(localNode.data+" ");
            //前序遍历左子树
            frontOrder(localNode.leftChild);
            //前序遍历右子树
            frontOrder(localNode.rightChild);
        }
    }

    /**
     * 中序遍历
     * @param localNode
     */
    public void inOrder(Node localNode){
        if (localNode != null){
            //中序遍历左子树
            frontOrder(localNode.leftChild);
            //访问根节点
            System.out.println(localNode.data+" ");
            //中序遍历右子树
            frontOrder(localNode.rightChild);
        }
    }
    /**
     * 后序遍历
     * @param localNode
     */
    public void afterOrder(Node localNode){
        if (localNode != null){
            //后序遍历左子树
            frontOrder(localNode.leftChild);
            //后序遍历右子树
            frontOrder(localNode.rightChild);
            //访问根节点
            System.out.println(localNode.data+" ");
        }
    }

    /**
     * 查找中序后继节点
     * @param delNode
     * @return
     */
    public Node getSuccessor(Node delNode){
        Node successor =delNode;
        Node successorParent = delNode;
        Node current =delNode.rightChild;

        while (current != null){
            successorParent = successor;//保存父节点的引用
            successor =current;//保存当前节点的引用
            current = current.leftChild;
        }
        //将中序后继节点与删除节点替换
        if (successor != delNode.rightChild){
            successorParent.leftChild = successor.rightChild;//如果这个中序后继节点还有右子节点，将他变成这个中序后继节点位置
            successor.rightChild = delNode.rightChild;
        }
        return successor;
    }
    /**
     * 删除节点
     * @param value
     */
    public boolean delete(long value){
        //引用当前节点
        Node current =root;
        //引用当前节点父节点
        Node parent = root;
        //判断是否是左子节点
        boolean isLeftChild = false;
        //查找节点
        while (current.data!= value){
            parent=current;
            if (current.data > value){
                current = current.leftChild;
                isLeftChild = true;
            }else if(current.data < value) {
                current =current.rightChild;
                isLeftChild = false;
            }else {
                return false;
            }
        }

        //删除节点
        if (current.leftChild == null && current.rightChild ==null){//删除叶子节点，该节点没有子节点
            if (current == root){
                root = null;
            }
            //如果是父节点的左子节点
            else if (isLeftChild){
                parent.leftChild=null;
            }else {
                parent.rightChild=null;
            }
            return true;
        }else if (current.rightChild == null){//如果节点只有一个左节点
            if (current == root){//跳过待删除节点，让待删除节点的左子节点变成根节点
                root=current.leftChild;
            }
            else if (isLeftChild){//如果待删除节点是左子节点，让父节点的左子节点等于待删除节点的左子节点
                parent.leftChild=current.leftChild;
            }else {//如果待删除节点是右子节点，让父节点的右子节点等于待删除节点的左子节点
                parent.rightChild=current.leftChild;
            }
            return true;
        }else if (current.leftChild == null){//如果节点只有一个右节点
            if (current == root){//跳过待删除节点，让待删除节点的右子节点变成根节点
                root=current.rightChild;
            }else if (isLeftChild){//如果待删除节点是左子节点，让父节点的左子节点等于待删除节点的右子节点
                parent.leftChild =current.rightChild;
            }else {
                parent.rightChild=current.rightChild;
            }
            return true;
        }else {//如果有两个子节点
            Node successor =getSuccessor(current);
            if (current == root){
                root =successor;
            }else if (isLeftChild){
                parent.leftChild=successor;
            }else {
                parent.rightChild=successor;
            }
            successor.leftChild=current.leftChild;

        }
        return false;
    }
}

7.7 哈夫曼树和哈夫曼编码

哈夫曼编码(Huffman Coding)是一种编码方法，哈夫曼编码是可变字长编码(VLC)的一种。

哈夫曼编码使用变长编码表对源符号（如文件中的一个字母）进行编码，其中变长编码表是通过一种评估来源符号出现机率的方法得到的，出现机率高的字母使用较短的编码，反之出现机率低的则使用较长的编码，这便使编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。

哈夫曼编码需要依赖哈夫曼树来实现，哈夫曼树又称为最优二叉树，哈夫曼树是带权路径长度最小的树。

下面演示创建哈夫曼树

假设有a b c d e五个字符，权重分别为50, 10, 16, 8, 12，现在将它们生成一颗哈夫曼树。

先找出权重最小的两个字符构成一棵二叉树，这里最小的为d 和 b

它们父节点的权重是两者相加的结果，现在将b和d的权重从最序列( 50, 10, 16, 8, 12)中删除，再将它们的父节点的权重加入为50,16,12,18重复直到序列中只有一个元素为止

最后生成的哈夫曼树为

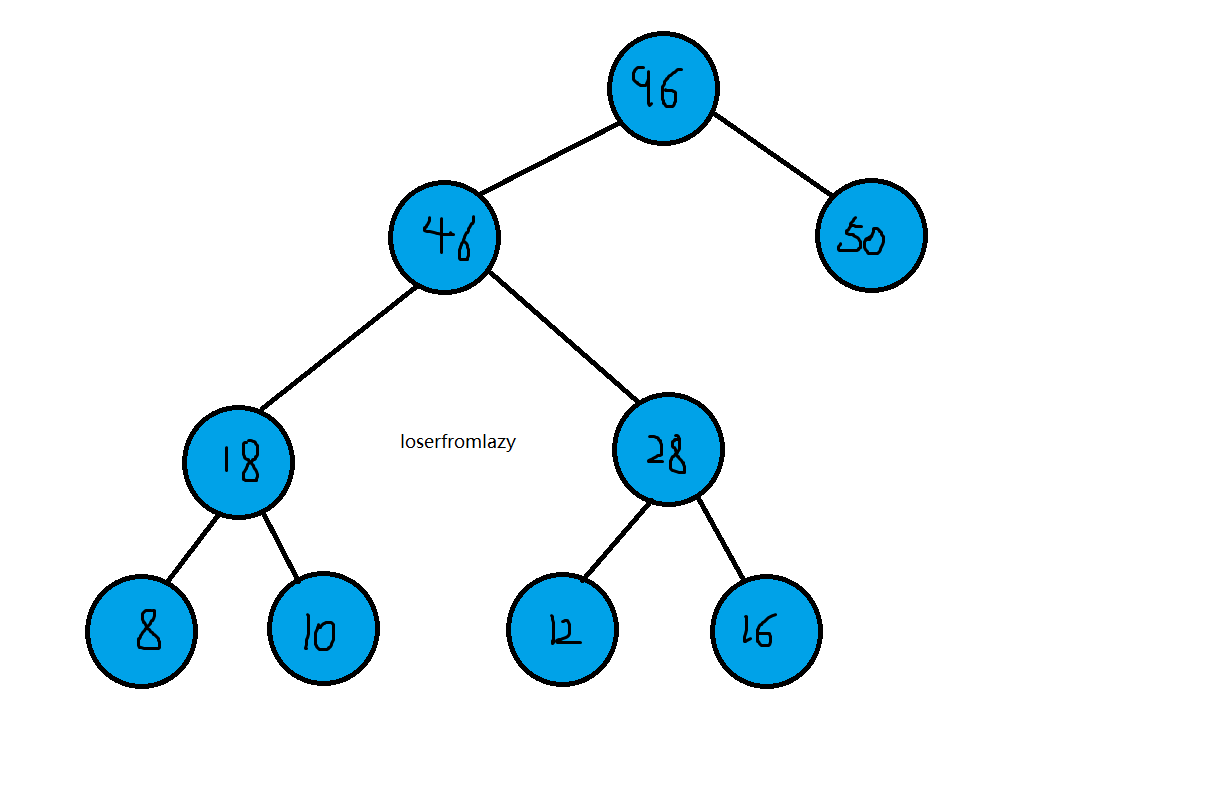
可见，根节点到权重最高的字符所需的路径最短。

八. 红黑树

红黑树（Red Black Tree） 是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。

红黑树过于复杂，这里只做简单介绍。

8.1 简介

二叉树的问题

二叉树作为数据存储工具有很大的优势，可以快速插入删除和查找数据项，但这仅仅针对于插入随机数据，如果插入的数据是有序的，那么速度将变得特别慢。

如下图，如果是顺序数组，那么会造成二叉树的右节点为空造成浪费。

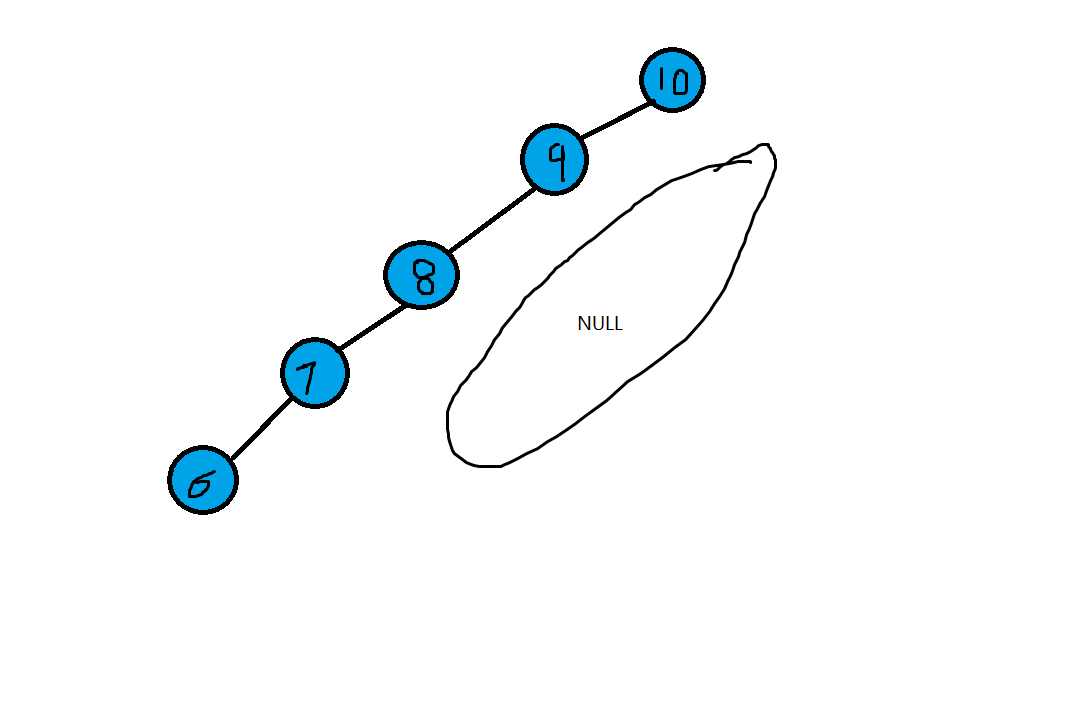
平衡树和非平衡树
平衡树：平衡树是二叉搜索树和堆合并构成的数据结构，它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

常见有红黑树、AVL树等等。

因为插入随机的数据可以保证树是大部分平衡或完全平衡，如果插入有序的数那么树将变得不平衡

红黑树
红黑树的节点都有颜色，且在插入或删除的过程中须保持颜色的不同排列规则，此规则就是红黑规则：

1. 每个节点不是红色就是黑色。
2. 根节点总是黑色的
3. 如果节点是红色的，那么他的子节点必须是黑色的。（反之不一定，即从根节点到所有路径不能有两个连续的红色节点。）
4. 从根节点到叶节点的每条路径，必须包含相同数目的黑色节点。（或者说从根节点到叶结点路径上的黑色的高度必须相同）

8.2 红黑树的纠正

如果出现违反规则进行自我纠正，纠正有两种方式，改变节点的颜色或者是进行旋转操作（旋转包括左旋和右旋）。

改变节点颜色

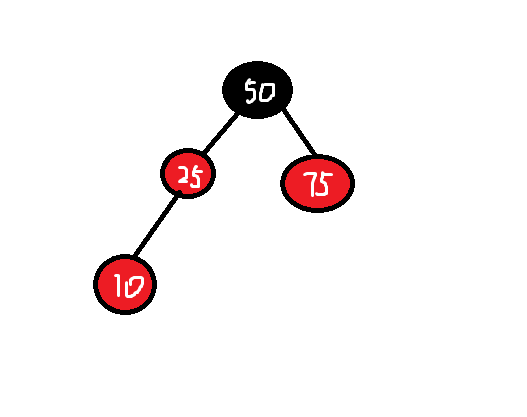
如上面所示，将插入一个新的节点10，通常新插入的节点为红色，此时插入违反规则三，如果将10这个节点改为黑色那么又将违反规则四。

这时如果将25改为黑色，那么75这个兄弟节点也需要改为黑色，50这个节点是根节点只能为黑色，所以变为如下:

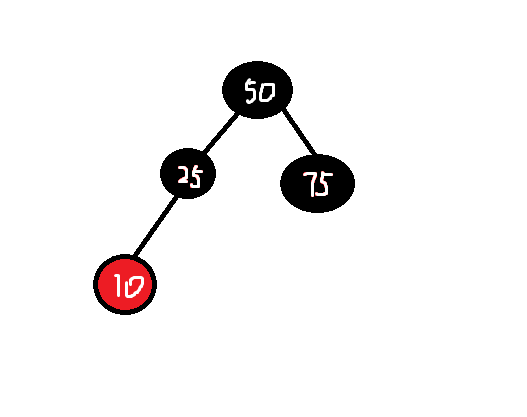
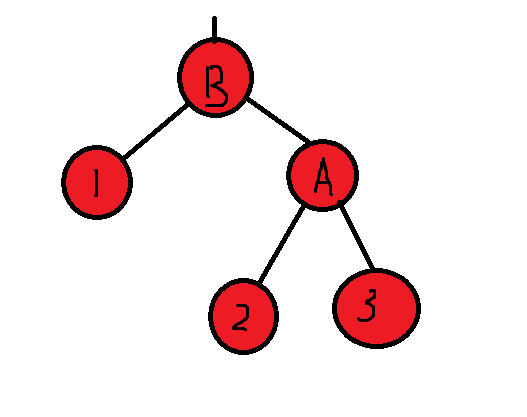
左旋

A为父节点，B为孩子节点。左旋操作后，B节点代替A节点的位置，A节点成为B节点的左孩子，B节点的左孩子成为A节点的右孩子。

旋转前：

旋转后：

右旋

节点本身是不会旋转的，旋转改变的是节点之间的关系，选择一个节点作为旋转的顶端。A为父节点，B为孩子节点。右旋操作后，B节点代替A节点的位置，A节点成为B节点的右孩子，B节点的右孩子成为A节点的左孩子。

旋转前：

旋转后：

九.哈希表

Hash表也称散列表，也有直接译作哈希表，Hash表是一种根据关键字值（key - value）而直接进行访问的数据结构。它提供了快速的插入和查找操作。它基于数组，通过把关键字映射到数组的某个下标来加快查找速度。

9.1 哈希化（哈希函数）

若结构中存在和关键字K相等的记录，则必定在f(K)的存储位置上。由此，不需比较便可直接取得所查记录。称这个对应关系f为散列函数Hash function)，按这个事先建立的表为散列表。

例如字典，可以通过前面的拼音快速定位到这个字在多少页，那么如何简历这个字与页数的关系呢？

1. 直接将关键字转换成索引

   Info.java
   /**
    * 员工信息
    */
   public class Info {
       private int key;
       private String name;
   
       public Info(int key,String name){
           this.key=key;
           this.name=name;
       }
   
       public int getKey() {
           return key;
       }
   
       public void setKey(int key) {
           this.key = key;
       }
   
       public String getName() {
           return name;
       }
   
       public void setName(String name) {
           this.name = name;
       }
   }
   HashTable.java
   public class HashTable {
       private Info[] arr;
       public HashTable(){
           arr =new Info[100];
       }
       public HashTable(int maxSize){
           arr =new Info[maxSize];
       }
   
       /**
        * 插入数据
        * @param info
        */
       public void insert(Info info){
           arr[info.getKey()]=info;
       }
       /**
        * 查找数据
        * @param key
        * @return
        */
       public Info find(int key){
           return arr[key];
       }
   }
   

   上面的例子可以看到我们存储员工信息，因为员工编号是int所以直接使用关键字作为索引。但这样的hash表肯定是不全面的因为只能有int类型的key，所以继续向下看。

2. 将单词转换成索引

   ​ 如果索引是String类型的话，这时就需要将这个String类型转换成索引。这时有以下几种方法：

   1. 将字母转换成ASCII码相加

      Info.java
      public class Info {
          private String key;//修改类型为String
          private String name;
      	//。。。略
      }
      HashTable.java
      public class HashTable {
          private Info[] arr;
          public HashTable(){
              arr =new Info[100];
          }
          public HashTable(int maxSize){
              arr =new Info[maxSize];
          }
          /**
           * 插入数据
           * @param info
           */
          public void insert(Info info){
              arr[hashCode(info.getKey()) ]=info;
          }
          /**
           * 查找数据
           * @param key
           * @return
           */
          public Info find(String key){
              return arr[hashCode(key) ];
          }
          //新增key值哈希化的方法
          public int hashCode(String key){
              int hashValue =0;
              for (int i=0;i<key.length();i++){
                  int letter = key.charAt(i)-96;//小写字母a的ASCII为97，这样就可以使a等于1
                  hashValue += letter;
              }
              return hashValue;
          }
      }
      

      这种方法存在缺陷比如abc和bbb作为key值两者的key值相等，所以这种方法key值有限，不适合我们使用，所以继续向下看。

   2. 幂的连乘

      我们将单词表示的数拆成数列，用27 的幂乘以这些位数（因为有26个字母加空格），然后把乘积相加，这样就得出了每个单词独一无二的数字。

      比如abc可以等于1*27^2 + 2*27^1 + 3*27^0

      public int hashCode(String key){
              //数的相加
              /*int hashValue =0;
              for (int i=0;i<key.length();i++){
                  int letter = key.charAt(i)-96;//小写字母a的ASCII为97，这样就可以使a等于1
                  hashValue += letter;
              }
              return hashValue;*/
      
              //幂的连乘
              int hashValue =0;
              int pow27=1;
              for (int i=key.length()-1;i>=0;i--){
                  int letter = key.charAt(i)-96;//小写字母a的ASCII为97，这样就可以使a等于1
                  hashValue += letter*pow27;
                  pow27*=27;
              }
              return hashValue;
          }
      

      以上是对hashCode方法的修改，但这样计算出来的hashValue的值非常大，所以我们需要进行压缩。

   3. 压缩可选值

      public int hashCode(String key){
              //压缩
              BigInteger hashValue = new BigInteger("0");
              BigInteger pow27 = new BigInteger("1");
              for (int i = key.length()-1; i >=0 ; i--) {
                  int letter = key.charAt(i)-96;
                  BigInteger letterB = new BigInteger(String.valueOf(letter));
                  hashValue = hashValue.add(letterB.multiply(pow27));
                  pow27=pow27.multiply(new BigInteger(String.valueOf(27)));
              }
              return hashValue.mod(new BigInteger(String.valueOf(arr.length))).intValue();
          }
      

      以上是对hashCode的修改，将int转换成BigInteger类型然后取余进行压缩。转换成BigInteger主要是因为在乘的过程中数字过大会超过int的范围。这里为什么要取余呢？是因为如果想将1-199（大数字）的数字压缩成1-9（小数字）的数字，1-9有10（小数字的范围）个数，所以当被10整除时，余数在0-9之间，这样就可以完成压缩，即

      小数字=大数字hashValue%范围

      这就是哈希函数。它把一个大范围的数字哈希（转化）成一个小范围的数字，这个小范围的数对应着数组的下标。使用哈希函数向数组插入数据后，这个数组就是哈希表。

冲突

压缩后可能出现此问题，即不能保证每个单词都映射到数组的空白单元。比如1-199压缩到0-9，可能会出现重复。

压缩中小数字每一个数可能对应多个数据，例如arr数组大小为100，这时a通过幂的连乘和压缩后得1，而ct在经过运算后也是1，这样就导致插入时key重复，如下面例子（此处的HashTable为上面自己实现的类）：

HashTable ht =new HashTable();
ht.insert(new Info("a","zhangsan"));
ht.insert(new Info("ct","lisi"));

这样就会导致ct在插入后会覆盖掉上面以a为key的zhangsan。这就是冲突的发生。

解决办法：开放地址法和链地址法

9.2 开放地址法

当冲突发生时，通过查找数组的一个空位，并将数据填入，而不在用哈希函数算出来的值当作数组下标，这种方法叫做开放地址法。那么怎么查找空位呢，这里有三种方法，线性探测、二次探测以及双散列法。公式为：

Hi=(H(key)+di)%m 其中Hi为第i次冲突产生的哈希函数；其中i=1，2，…，s，H(key)为哈希函数，m为哈希表长，di为增量序列。

9.2.1线性探测

比如要插入的位置是1，但是他已经被占用了，这时就让数组下标依次递增,代码如下：

import java.math.BigInteger;
/**
 * 开放地址法
 */
public class MyHashTable {
    private Info[] arr;

    public MyHashTable(){
        arr =new Info[100];
    }

    public MyHashTable(int maxSize){
        arr =new Info[maxSize];
    }

    /**
     * 插入数据
     * @param info
     */
    public void insert(Info info){
        //关键字
        String key = info.getKey();
        //关键字的哈希值
        int hashValue = hashCode(key);
        //如果数组索引被占用且是合法未被删除的数据
        while (arr[hashValue]!=null && arr[hashValue].getName()!=null){
            //累加
            ++hashValue;
            //万一hashValue超出数组范围那么就再次取模从头开始
            hashValue %= arr.length;
        }
        arr[hashValue]=info;
    }

    /**
     * 查找数据
     * @param key
     * @return
     */
    public Info find(String key){
        int hashValue =hashCode(key);
       /* 插入时如果此处有数据，那么一定会向下递增寻找空地址，所以从此处到要找到的数据之间不会有空着的地方*/
        while (arr[hashValue] != null){
            if (arr[hashValue].getKey().equals(key)){
                return arr[hashValue];
            }
            ++hashValue;
            hashValue %= arr.length;
        }

        return null;
    }

    /**
     * 删除数据
     * @param key
     * @return
     */
    public Info delete(String key){
        int hashValue = hashCode(key);
        while (arr[hashValue] != null){
            if (arr[hashValue].getKey().equals(key)){
                Info tmp =arr[hashValue];
                tmp.setName(null);
                return tmp;
            }
            ++hashValue;
            hashValue %= arr.length;
        }
        return  null;
    }

    public int hashCode(String key){
        //压缩
        BigInteger hashValue = new BigInteger("0");
        BigInteger pow27 = new BigInteger("1");
        for (int i = key.length()-1; i >=0 ; i--) {
            int letter = key.charAt(i)-96;
            BigInteger letterB = new BigInteger(String.valueOf(letter));
            hashValue = hashValue.add(letterB.multiply(pow27));
            pow27=pow27.multiply(new BigInteger(String.valueOf(27)));
        }
        return hashValue.mod(new BigInteger(String.valueOf(arr.length))).intValue();
    }
}

当哈希表变得比较满时，我们每插入一个新的数据，都要频繁的探测插入位置，因为可能很多位置都被前面插入的数据所占用了，这称为聚集。数组填的越满，聚集越可能发生。

装填因子
已填入哈希表的数据项和表长的比率叫做装填因子，比如有10000个单元的哈希表填入了6666 个数据后，其装填因子为 2/3。当装填因子不太大时，聚集分布的比较连贯，而装填因子比较大时，则聚集发生的很大了。

开放地址法要求散列表的装填因子α≤l，实用中取α为0.5到0.9之间的某个值为宜。

9.2.2二次探测（平方探测）

当装填因子比较大时，会频繁的产生聚集，而二次探测就是防止发生聚集的一种方式。

如果哈希函数计算的原始下标是x, 线性探测就是x+1, x+2, x+3；而二次探测就是x+1, x+4, x+9, x+16；也就是说二次探测不是逐一递增而是递增步数的平方。

二次探测虽然消除了线性探测的聚集问题，但是会产生二次聚集，比如说有a，b，c，d四个数他们的映射都是6，那么a就要以1为步长探测，b就是以4为步长探测，都一个数据就要以更长的步长探测，这就是二次聚集。

二次聚集不常用，更多使用双散列法

9.2.3双散列法

也叫双散列函数探查法，这时开放地址法中最好的方法之一，就是该方法使用了两个散列函数h(key)和h1(key)，故也称为双散列函数探查法。

9.3链地址法

在哈希表的每一个单元设置链表。某个数据项的关键字还是像通常映射到哈希表中，而数据项本身插入到每一个单元的链表中。

public class LianHash {
    private LinkList[] arr;

    public LianHash(){
        arr =new LinkList[100];
    }

    public LianHash(int maxSize){
        arr =new LinkList[maxSize];
    }

    /**
     * 插入数据
     * @param info
     */
    public void insert(Info info){
        //关键字
        String key = info.getKey();
        //关键字的哈希值
        int hashValue = hashCode(key);
        if (arr[hashValue]==null){
            arr[hashValue] =new LinkList();
        }
        arr[hashValue].insertFirst(info);

    }

    /**
     * 查找数据
     * @param key
     * @return
     */
    public Info find(String key){
        int hashValue =hashCode(key);
        return arr[hashValue].find(key).info;
    }

    /**
     * 删除数据
     * @param key
     * @return
     */
    public boolean delete(String key){
        int hashValue = hashCode(key);
        return arr[hashValue].delete(key);
    }

    public int hashCode(String key){
        //压缩
        BigInteger hashValue = new BigInteger("0");
        BigInteger pow27 = new BigInteger("1");
        for (int i = key.length()-1; i >=0 ; i--) {
            int letter = key.charAt(i)-96;
            BigInteger letterB = new BigInteger(String.valueOf(letter));
            hashValue = hashValue.add(letterB.multiply(pow27));
            pow27=pow27.multiply(new BigInteger(String.valueOf(27)));
        }
        return hashValue.mod(new BigInteger(String.valueOf(arr.length))).intValue();
    }
}

上述代码中LinkList链表的代码，此代码与之前单向链表类似。

十. 图

10.1 定义

图的定义

图示一种和树想象的数据结构，图通常有个固定的形状，这是由物理或抽象的问题所决定的。

邻接

如果两个顶点被同一条边连接，就称这两个邻接的，如上图I和G是邻接的，单I和F就不是

路径

路径是边的序列，比如说从顶点B到J的路径为BAEJ，当然还有其他路径BCDJ、BACDJ等。

连通图和非连通图

至少有一条路径可以连接所有顶点，那么这个图是连通的。

有向图和无向图

如果图中的边没有方向，可以从任意一边到达另一边，成为无向图，如双向高速公路，A城市到B城市可以开车从A驶向B，也可以开车从B城市驶向A城市。但是如果只能从A城市驶向B城市的图，那么则称为有向图。

有权图和无权图

图中的边被赋予值，值是一个数字，它可以代表两个顶点的物理距离，或是一个点到另一个点的时间等等，这样的图被称为带权图；如果没有被赋值这成为无权图。

在这里我们讨论无权无向图。

10.2 在程序中表示图

顶点

顶点对象可以用顶点类来表示，顶点对象能放在数组中，用下标指示，也可以·放在链表或其他数据结构中。

/**
 * 顶点类
 * @author Loserfromlazy
 */
public class Vertex {
    public char label;//
    public boolean wasVisited;//表示是否被访问

    public Vertex(char label){
        this.label = label;
        wasVisited = false;
    }

}

边

上面的各种数据结构中，大多数树都是每个节点包好其他子节点的引用，比如红黑树、二叉树。然而图不像树，图没有固定的结构，图的每一个顶点可以与任意多个顶点项链，所以用以下两种方式表视图：邻接表和邻接矩阵。

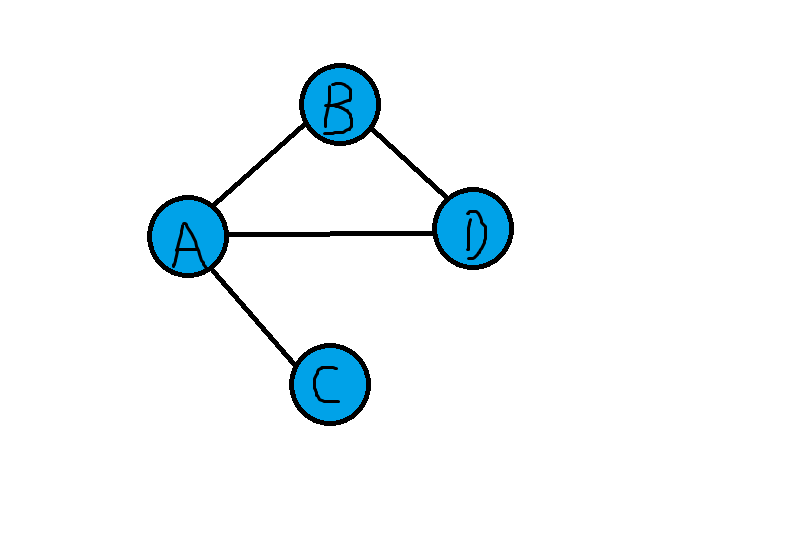
邻接矩阵：

邻接矩阵是一个二维数组，数据项表示两点是否存在便，图中有N个顶点，邻接矩阵救赎N*N的数组上图的邻接矩阵如下

	A	B	C	D
A	0	1	1	1
B	1	0	0	1
C	1	0	0	0
D	1	1	0	0

1表示有边，0表示没有边，也可以用布尔变量表示。顶点与自身相连是0，所以左上到右下对角线都为0.

邻接表：

邻接表是一个链表数组（或者是链表的链表），每个单独的链表表示了有哪些顶点与当前顶点邻接。

顶点	包含邻接顶点的链表
A	B->C->D
B	A->D
C	A
D	A->B

10.3 搜索

在图中最基本的操作之一就是搜索一个顶点可以到达那些顶点，有两种方法可以用于搜索图：分别是深度优先搜索（DSF）和广度优先搜索（BSF）。深度优先搜索通过栈来实现，而广度优先搜索通过队列来实现。

深度优先搜索

1. 如果可以，访问一个邻接的未访问顶点，标记它并放入栈中。
2. 当不能执行第一条，如果栈不为空，就弹出一个顶点。
3. 如果不能执行第一条和第二条，就完成了搜索过程。

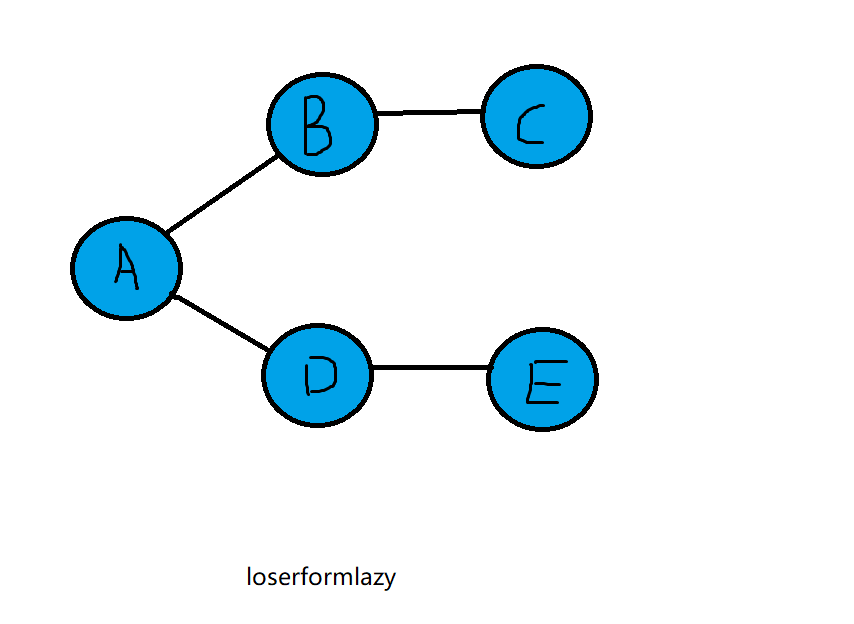
以上图为例，深度优先算法结果为ABCDE（此结果以A为第一点）

广度优先搜索

1. 访问下一个未访问的临界点，这个顶点必须是当前顶点的邻接点，标记它，并将它插入到队列中
2. 如果已经没有未访问的邻接点而不能执行规则1时，从队列头取出一个顶点，并使其成为当前顶点。
3. 如果因为队列为空而不能执行规则2，则搜索结束。

以上图为例，广度优先算法的结果为：ABDCE（此结果以A为第一点）

代码实现

深度优先搜索的栈

/**
 * 深度优先搜索使用的栈
 */
public class Stack {

    private int [] arr;
    private int top;

    public Stack(){
        arr = new int[10];
        top=-1;
    }

    public Stack(int maxSize){
        arr = new int[maxSize];
        top=-1;
    }

    public void push(int value){
        arr[++top]=value;
    }

    public int pop(){
        return arr[top--];
    }

    public int peek(){
        return arr[top];
    }

    public boolean isEmpty(){
        return top == -1;
    }
}

广度优先搜索使用的队列

/**
 * 广度优先搜索使用的队列
 */
public class Queue {

    private int[] arr;
    private int front;
    private int end;

    public Queue(){
        arr = new int[10];
        end=-1;
        front =0;
    }

    public Queue(int maxSize){
        arr = new int[maxSize];
        end=-1;
        front=0;
    }

    public void insert(int value){
        if (end == arr.length-1){
            end=-1;
        }
        arr[++end] = value;
    }

    public int remove(){
        int value =arr[front++];
        if (front==arr.length){
            front=0;
        }
        return value;
    }

    public int peek(){
        return arr[front];
    }
    
    public boolean isEmpty(){
        return (end+1==front || front+arr.length-1 ==end );
    }
}

Graph.java（图类代码）

package ch10;


/**
 * 图类
 *
 */
public class Graph {

    private final int MAX_NUMS = 20;//最大顶点个数
    private Vertex vertexArr[];//用来存储顶点的数组
    private int adjMat[][];//邻接矩阵
    private int VertexNum;//顶点个数
    private Stack stack;//用于深度优先搜索的栈
    private Queue queue;//用于广度优先搜索的队列

    /**
     * 顶点类
     * @author Loserfromlazy
     */
    class Vertex {
        public char label;//
        public boolean isVisited;//表示是否被访问

        public Vertex(char label){
            this.label = label;
            isVisited = false;
        }
    }

    public Graph(){
        vertexArr = new Vertex[MAX_NUMS];
        adjMat = new int[MAX_NUMS][MAX_NUMS];
        VertexNum =0;
        //初始化邻接矩阵
        for (int i = 0; i <MAX_NUMS ; i++) {
            for (int j = 0; j <MAX_NUMS ; j++) {
                adjMat[0][0]=0;
            }
        }
        stack = new Stack();
        queue = new Queue();
    }

    /**
     * 将顶点添加到数组中，是否访问设置为未访问
     * @param lab
     */
    public void addVertex(char lab){
        vertexArr[VertexNum++] = new Vertex(lab);
    }

    /**
     * 用邻接矩阵表示边，无权无向图是对称的，两部分要赋值
     * @param start
     * @param end
     */
    public void addEdge(int start , int end){
        adjMat[start][end]=1;
        adjMat[end][start]=1;
    }

    public void  displayVertex(int val){
        System.out.println(vertexArr[val].label);
    }

    /**
     * 找到与某一顶点邻接且未被访问的顶点
     * @param v
     * @return
     */
    public int getAdjUnvisitedVertex(int v){
        for (int i = 0; i <VertexNum ; i++) {
            if (adjMat[v][i]==1 && vertexArr[i].isVisited==false){
                return i;
            }
        }
        return -1;
    }

    /**
     * 深度优先算法
     * 1. 用peek()方法检查栈顶的顶点
     * 2. 用getAdjUnvisitedVertex()方法找到当前 栈 顶点邻接且未被访问的顶点
     * 3. 第二步方法返回值不等于-1 则找到下一个未访问的邻接顶点，访问这个顶点，并入栈
     *    如果第二部方法返回值等于-1 ，则没有找到，出栈
     */
    public void depthFirstSearch(){
        //从第一个顶点开始访问
        vertexArr[0].isVisited=true;
        displayVertex(0);//显示第一个顶点
        stack.push(0);//将第一个顶点放入栈中

        while (!stack.isEmpty()){
            //找到栈顶邻接且未访问的点
            int v = getAdjUnvisitedVertex(stack.peek());
            if (v == -1){
                stack.pop();
            }else {
                vertexArr[v].isVisited =true;
                displayVertex(v);
                stack.push(v);
            }
        }
        //栈访问完毕，充值所有标记位
        for (int i = 0; i <VertexNum ; i++) {
            vertexArr[i].isVisited =false;
        }
    }

    /**
     * 广度优先算法
     * 1.用remove()方法检查队列的队头
     * 2.试图找到这个顶点的未访问的邻接点
     * 3.如果未找到。则顶点出列
     * 4.如果找到了，访问这个顶点，并把它放入队列中
     */
    public void breadthFirstSearch(){
        vertexArr[0].isVisited =true;
        displayVertex(0);
        queue.insert(0);
        int v2;

        while(!queue.isEmpty()){
            int v1 =queue.remove();
            while((v2 = getAdjUnvisitedVertex(v1))!=-1){
                vertexArr[v2].isVisited =true;
                displayVertex(v2);
                queue.insert(v2);
            }
        }

        //搜索完毕，初始化
        for (int i = 0; i <VertexNum ; i++) {
            vertexArr[i].isVisited =false;

        }
    }

    public static void main(String[] args) {
        Graph graph = new Graph();
        graph.addVertex('A');
        graph.addVertex('B');
        graph.addVertex('C');
        graph.addVertex('D');
        graph.addVertex('E');

        graph.addEdge(0, 1);//AB
        graph.addEdge(1, 2);//BC
        graph.addEdge(0, 3);//AD
        graph.addEdge(3, 4);//DE

        System.out.println("深度优先搜索算法 :");
        graph.depthFirstSearch();//ABCDE

        System.out.println();
        System.out.println("----------------------");

        System.out.println("广度优先搜索算法 :");
        graph.breadthFirstSearch();//ABDCE
    }
}

10.4 最小生成树

对于一张图，我们有一个定理：n个点用n-1条边连接，形成的图形只可能是树。我们可以这样理解：树的每一个结点都有一个唯一的父亲，也就是至少有n条边，但是根节点要除外，所以就是n-1条边。还有一种理解：树里不存在环，那么既要连接n个点又不能形成环，只能用n-1条边。

那么，对于一张n个点带权图，它的生成树就是用其中的n-1条边来连接这n个点，那么最小生成树就是n-1条边的边权之和最小的一种方案，简单的理解，就是用让这张图只剩下n-1条边，同时这n-1条边的边权总和最小。