目录
- 矩阵向量求导定义
- 矩阵向量求导布局
机器学习中很多地方用到了标量,向量和矩阵之间的求导,计算求导确实非常麻烦,三个两两结合,就有9中基本形态,再加上转置,就更加晕乎了,因此作为后续学习基础,这个放到机器学习最前面作为先导知识。具体求导内容可见:
张贤达的《矩阵分析与应用》,电子档文本如下:
链接:https://pan.baidu.com/s/1iIcqAyJ1cfi2icdwgay0kw 提取码:rcwx
一、矩阵向量求导定义
求导其实高中就学过,基本都是标量对标量求导,也即是下图中的第一种形式,很简单就不展开。所谓向量对标量的求导,其实就是向量里的每个分量分别对标量求导,最后把求导的结果排列在一起,按一个向量表示而已。类似的结论也存在于标量对向量的求导,向量对向量的求导,向量对矩阵的求导,矩阵对向量的求导,以及矩阵对矩阵的求导等。
若没有特殊说明,默认情况定义如下:求导的自变量用x表示标量,x表示n维向量,X表示m×n维度的矩阵,求导的因变量用y表示标量,y表示m维向量,Y表示p×q维度的矩阵。默认向量为列向量,若是行向量,本文全部使用对应字母的转置表示。
根据求导的自变量和因变量是标量,向量还是矩阵,我们有9种可能的矩阵求导定义,如下:
|
自变量因变量 |
标量y |
向量y |
矩阵Y |
|
标量x |
∂y/∂x |
∂y/∂x |
∂Y/∂x |
|
向量x |
∂y/∂x |
∂y/∂x |
∂Y/∂x |
|
矩阵X |
∂y/∂X |
∂y/∂X |
∂Y/∂X |
但是向量和矩阵表示又区分行和列不同情况,实际也就是转置不同,需要统一标准,才能阅读方便,一般称之为求导布局。
二、 矩阵向量求导布局
最基本的求导布局有两个:分子布局(numerator layout)和分母布局(denominator layout )。总体原则:根据保持与前面向量或矩阵为一致作为默认形式
2.1 分子布局(numerator layout)
一种解释:分子为 y 或者分母为 xT (即,分子为列向量或者分母为行向量)
另一种理解:以分子为主,求导的结果的维度和分子的维度是一致的。
如果向量y是一个m维的列向量,那么求导结果∂y/∂x也是一个m维列向量;
如果向量y是一个m维的行向量,那么求导结果∂y/∂x也是一个m维行向量。
2.2 分母布局(denominator layout )
一种解释:分子为 yT 或者分母为 x (即,分子为行向量或者分母为列向量)
另一种理解:对于分母布局来说,我们求导结果的维度以分母为主
如果向量y是一个m维的列向量,那么求导结果∂y/∂x是一个m维行向量;
如果向量y是一个m维的行向量,那么求导结果∂y/∂x是一个m维列向量。
2.3 举例说明:
总体来说还是有点绕,统一举例列表如下所示。
2.3.1 分子布局
标量/向量(行向量):

向量 (列向量)/标量:默认形式
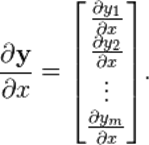
向量/向量: (分子为列向量横向平铺,分母为行向量纵向平铺)默认形式 称为雅克比 (Jacobian)矩阵

标量/矩阵: (注意这个矩阵部分是转置的,而下面的分母布局是非转置的)

矩阵/标量:默认形式
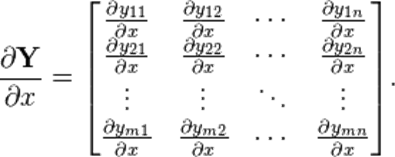
2.3.2 分母布局
标量/向量: (分母的向量为列向量)默认形式
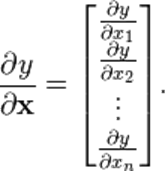
向量/标量: (分子的向量为行向量)

向量/向量: (分子为行向量纵向平铺,分母为列向量横向平铺)

标量/矩阵: (矩阵部分为原始矩阵)默认形式

2.3.3 汇总
第一种太简单,不写了,后面三种情况太难,后续再展开。均有斜杠表示。我么按照列向量来举例子,行向量取转置即可。
|
自变量因变量 |
标量y |
列向量y(m维) |
矩阵Y(p × q) |
|
标量x |
/ |
∂y/∂x 分子布局:m维列向量(默认布局) 分母布局:m维行向量 |
∂Y/∂x 分子布局:p × q矩阵(默认布局) 分母布局:q × p矩阵 |
|
列向量x(n维) |
∂y/∂x 分子布局:n维行向量 分母布局:n维列向量(默认布局)
|
∂y/∂x 分子布局:m × n雅可比矩阵(默认布局) 分母布局:n × m梯度矩阵 |
/ |
|
矩阵X (p × q) |
∂y/∂X 分子布局:q × p矩阵 分母布局:p × q矩阵(默认布局) |
/ |
/ |
主要来自: