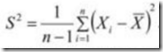《数据挖掘导论》笔记（三）

探索数据

数据探索有助于选择合适的数据预处理和数据分析技术。它甚至可以处理一些通常由数据挖掘解决的问题，例如，有时可以通过对数据进行直观检查来发现模式。此外数据探索中使用的某些技术（如可视化）可以用于理解和解释数据挖掘结果。

本章包括三个主题：汇总统计、可视化和联机分析处理（OLAP）.

汇总统计（如值集合的均值和标准差）和可视化技术（如直方图和散布图）是广泛用于数据探索的标准方法。OLAP是一种新近开发的包含一系列考察多维数组数据的技术。OLAP的分析功能集中在从多维数据数组中创建汇总表的各种方法。

本章涵盖的主题与探测性数据分析（EDA）有许多重叠。像EDA一样，本章特别强调可视化，而与EDA不同的是，本章并不包含诸如聚类分析和异常检测等主题。

汇总统计

汇总统计是量化的（如均值和标准差），用单个数或数的小集合捕获可能很大的值集的各种特征。

频率和众数

值v的频率定义为           frequency（v）=具有属性值v的对象数/m

分类属性的众数是具有最高频率的值。

百分位数

对于有序数据，考虑值集的百分位数更有意义。具体的说，给定一个有序的或连续的属性x和0与100之间的数p，第p个百分位数x_p是一个x值，使得x的p%的观测值小于x_p

位置度量：均值和中位数

对于连续数据，两个使用最广发的汇总统计是均值和中位值，他们是值集位置的度量

尽管有时将均值解释为值集的中间，但是仅当值以对称方式分布时，才是对的。如果值的分布是倾斜的，则中位数是中间的一个更好的指示符。此外，均值对于离群值很敏感；对于包含离群值的数据，中位数可以再次更稳健地提供值集中间的估计。

为了克服传统均值定义的问题，有时使用截断均值概念。指定0和100之间的百分位数p,丢弃高端和低端（p/2）%的数据，然后用常规的方法计算均值，所得的结果即是截断均值。中位数是p=100%时的截断均值，而标准均值是对应于p=0%的截断均值。

散布度量：极差和方差

最简单的散布度量是极差。给定属性x,它具有m个值{x₁,…x_m}

极差range(X)=max(x)-min(x)=x_m-x₁

方差variance(x)=

均值可能被离群值扭曲，并且由于方差用均值计算，因此它也对离群值敏感。

绝对平均偏差：AAD

中位数绝对偏差：MAD

四分位数极差：IQR

多元汇总统计

协方差矩阵S:      s_ij=covariance(x_i,x_j)

两个属性的协方差是两个属性一起变化并依赖于变量大小的度量。协方差的值接近于0表明两个变量不具有（线性）关系，但是不能仅靠观察协方差的值来确定两个变量之间的关联程度。因为两个属性的相关性直接指出两个属性（线性）相关的程度，对于数据探索，相关性比协方差更可取。相关矩阵R的第ij个元素是数据的第i个和第j个属性之间的相关性

相关矩阵R:r_ij=correlation(x_i,x_j)=covariance(x_i,x_j)/s_is_j

s_i和s_j分别是xi和xj的方差

 

可视化

数据可视化是指以图形或表格的形式显示信息。成功的可视化需要将数据（信息）转换成可视形式，以便能够借此分析或报告数据的特征和数据项或属性之间的关系。可视化的目标是形成可视化信息的人工解释和信息的意境模型。

一般概念

1.表示：将数据映射到图形元素

可视化的第一步是将信息映射成可视形式，即将信息中的对象、属性和联系映射成可视的对象、属性和联系。也就是说，数据对象、它们的属性，以及数据对象之间的联系要转换成诸如点、线、形状和颜色等图形元素。

对象通常分为三种方法表示。首先如果只考虑对象的单个分类属性，则通常根据该属性的值将对象聚成类，并且把这些类作为表的项或屏幕的区域显示。其次，如果对象具有多个属性，则可以将对象显示为表的一行（或列），或显示为图的一条线。最后，对象常常解释为二维或三维空间中的点，其中点可能用几何图形表示，如圆圈、十字叉或方框。

对于属性，其表示取决于属性的类型，即取决于属性是标称的、序数的还是连续的（区间的或比率的）。序数的和连续的属性可以映射成连续的、有序的图形特征。对于分类属性，每个类别可以映射到不同的位置、颜色、形状、方位、修饰物或表的列。然而，对于标称属性，由于它的值是无序的，因此在使用具有与其值相关的固有序的图形特征时，就需要特别小心。换言之，用来表示序数值的图形元素通常有序，但标称值没有序。

通过图形元素表示的关系或者是显示的，或者是隐式的。对于图形数据，通常使用标准图形表示——点和点间的连线。如果点（数据对象）或连线（关系）具有子集的属性或特性，则这些属性也可以图示。

2.安排

对于好的可视化来说，正确选择对象和属性的可视化表示是基本的要求。在可视化显示中，项的安排也至关重要。

3.选择

可视化的另一个关键概念是选择，即删除或不突出某些对象和属性。具体说来，尽管只具有少数维的数据对象通常可以使用直截了当的方法映射成二维或三维图形表示。但是还没有令人完全满意和一般的方式表示具有许多属性的数据。同样，如果有很多数据对象，则可视化所有对象可能导致显示过于拥挤。如果有许多属性和许多对象，则情况会更加复杂。

处理很多属性的最常用方法是使用属性子集（通常是两个属性）。如果维度不太高，则可以构造双变量（双属性）图矩阵用于联合观察。或者说，可视化程序可以自动地显示一系列二维图，其中次序由用户或根据某种预定义的策略控制，让可视化二维图的集族提供数据的更完全的视图。

选择一对（或少数）属性的技术是一类维归约，并且有许多更复杂的维归约可以使用，如PCA。

当数据点的个数很多（例如超过数百个）或者数据的极差很大时，充分显示每个对象的信息是困难的，有些数据点可能遮掩其他数据点，或者数据对象可能占据不了足够多的像素来清楚地显示其特征。

技术

可视化技术对于分析地数据类型通常是专用性地。

尽管可视化具有专门性和特殊性，但仍有一般性方法可对可视化技术进行分类。一种分类是基于所涉及地属性个数（1，2，3或多），或者基于数据是否具有某种特殊地性质（如层次结构或图结构）。可视化方法也可以根据所涉及地属性类型分类。另一种分类是根据应用类型：科学的、统计学地或信息学地可视化。下面地讨论将使用三种类型：少量属性地可视化，具有时间和/或空间属性地数据可视化，以及具有大量属性的数据可视化。

1.少量属性的可视化

有些技术（如直方图）可以显示单个属性观测值分布，其他技术（如散布图）旨在显示两个属性值之间的关系。

茎叶图：可以用来观测一维整型或连续数据的分布

直方图：茎叶图是一种类型的直方图，该图通过将可能的值分散到箱中，并显示落入每个箱中的对象数，显示属性值的分布

相对概率直方图：用相对概率取代计数，然而，这只是一种y轴尺度的变化，直方图的形状并不改变。

Pareto直方图：它专门针对无序的分类数据，Pareto直方图与普通直方图一样，只是分类按计数排序，让计数从左到右递减。

二维直方图：它将每个属性划分成区间，而两个区间集定义值的二维长方体。

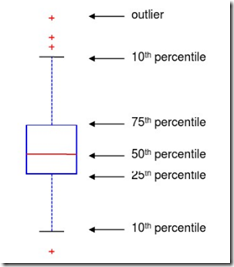
盒装图：盒的下端和上端分别指示第25和第75个百分位数，而盒中的线指示第50个百分位数的值，底部和顶部的尾线分别指示第10和第90个百分位数，离群值用“+”显示。盒状图相对紧凑，因此可以将许多盒装图放在一个图中。还可以使用占据较少空间的盒状图的简化版。

饼图：类似于直方图，但通常用于具有相对较少的值的分类属性。饼图使用圆的相对面积显示不同值的相对频率，而不是像直方图那样使用条形的面积或高度。

百分位数图和经验累计分布函数：累计分布函数（CDF）显示小于该值的概率。经验累计分布函数（ECDF）显示小于该值点的百分比，由于点的个数是有限的，经验累计分布函数是一个阶梯函数。

散布图：两个主要用途：1.图形化地显示两个属性之间的关系2.当类标号给出时，可以使用散布图考察两个属性将类分开的程度

2.可视化时间空间数据

数据常常有空间或时间属性

等高线图：对于某些三维数据，两个属性指定平面上的位置，而第三个属性具有连续值。对于这样的数据，一种有用的可视化工具是等高线图

曲面图：与等高线图一样，曲面图使用两个属性表示x和y的坐标，曲面图的第三个属性用来指示高出前两个属性定义的平面的高度。尽管这种图可能是有用的，但是这要求至少某个范围内，对于前两个属性值的所有组合，第三个属性值都有定义。

矢量场图：在某些数据中，一个特性可能同时具有值和方向。这种类型的图称作矢量图。

低维切片：考虑时间空间数据集，他记录不同地点和时间上的某种量，如温度或气压。这样的数据有四个维，不容易用迄今为止的图来显示。然而，通过显示一组图，每月一个，可以显示数据的各个”切片“。通过考察特定区域的逐月改变，就可能注意到所出现的变化，包括可能因为季节原因而导致的变化。

动画：无论是否涉及时间，处理数据切片的另一种方法是使用动画，基本思想是显示数据的相继二维切片

3.可视化高维据

矩阵：图像可以看作像素的矩阵阵列，其中每个像素用它的颜色和亮度刻画，数据矩阵是值的矩阵阵列，那么，将数据矩阵的每个元素与图像中的一个像素相关联，就可以把数据矩阵看作图像，像素的亮度和颜色由矩阵对应元素的值决定。

平行坐标系：每个属性一个坐标轴，但是与传统坐标系不同，平行坐标系不同的坐标轴是平行的，而不是正交的。此外，对象用线而不是用点表示，具体的说，对象每个属性的值映射到与该属性相关联的坐标轴上的点，然后将这些点连接起来形成代表该对象的线。平行坐标图的缺点之一是，在这种图中模式的检测可能取决于坐标轴的序。

星形坐标和Chernoff脸：显示多维数据的另一种方法是用非文字传达信息的符号——图示符或图标对对象编码。准确的说，对象的每个属性映射到图示符的一个特征，使得属性的值决定特征的准确性质。这样，只需要扫一眼我们就可以辨别两个对象的差异。星形坐标和Chernoff脸就是其中的两种方法。

OLAP和多维数据分析