HDU 4676 Sum Of Gcd 【莫队 + 欧拉】

任意门：http://acm.hdu.edu.cn/showproblem.php?pid=4676

Sum Of Gcd

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 908    Accepted Submission(s): 438

Problem Description

Given you a sequence of number a₁, a₂, ..., a_n, which is a permutation of 1...n.
You need to answer some queries, each with the following format:
Give you two numbers L, R, you should calculate sum of gcd(a[i], a[j]) for every L <= i < j <= R.

 

Input

First line contains a number T(T <= 10),denote the number of test cases.
Then follow T test cases.
For each test cases,the first line contains a number n(1<=n<= 20000).
The second line contains n number a₁,a₂,...,a_n.
The third line contains a number Q(1<=Q<=20000) denoting the number of queries.
Then Q lines follows,each lines contains two integer L,R(1<=L<=R<=n),denote a query.

 

Output

For each case, first you should print "Case #x:", where x indicates the case number between 1 and T.
Then for each query print the answer in one line.

 

Sample Input

1

5

3 2 5 4 1

3

1 5

2 4

3 3

 

Sample Output

Case #1:

11

4

0

 

Source

2013 Multi-University Training Contest 8

题意概括：

给出 1~N 的一个排列，M次查询，每次查询 L ~ R 内 GCD( ai, aj )  [ L <= i < j <= R ] 的总和。

解题思路：

又是涉及 GCD 又是 涉及区间查询，头有点大。

首先莫队处理区间查询，其次欧拉函数解决GCD问题。

根据：

 

那么用 gcd( ai, aj) 代替上式的 n，我们可以得到：

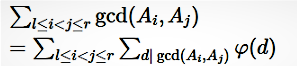
问题就转换成了求 d 的欧拉函数，其实 d 是有很多重复的，那么我们只要统计出当前查询区间【L，R】内 d 出现的次数然后乘上其欧拉函数值，所求的的答案就是区间GCD的总和。

欧拉函数值和对原序列的每一项的因数分解预处理时搞定。

AC code：

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define INF 0x3f3f3f3f
#define LL long long
using namespace std;

const int MAXN = 2e4+20;
int unit, a[MAXN], N, M, cnt[MAXN];
LL ans[MAXN], phi[MAXN];
vector<int>factor[MAXN];

struct Query
{
    int l, r, idx;
    friend bool operator < (const Query & a, const Query & b){
        int x1 = a.l/unit, x2 = b.l/unit;
        if(x1 != x2) return x1 < x2;
        return a.r < b.r;
    }
}Q[MAXN];

void init()
{
    for(int i = 1; i < MAXN; i++){      //分解因子
        for(int j = i; j < MAXN; j+=i)
            factor[j].push_back(i);
    }

    phi[1] = 1;                         //欧拉函数
    for(int i = 2; i < MAXN; i++){
        phi[i] = i;
    }
    for(int i = 2; i < MAXN; i++){
        if(phi[i] == i){
            for(int j = i; j < MAXN; j+=i)
                phi[j] = phi[j]/i*(i-1);
        }
        //puts("zjy");
    }
}

LL add(int x)
{
    LL res = 0;
    for(auto d : factor[x]) res+=cnt[d]*phi[d];
    for(auto d : factor[x]) cnt[d]++;
    return res;
}

LL del(int x)
{
    LL res = 0;
    for(auto d : factor[x]) cnt[d]--;
    for(auto d : factor[x]) res+=cnt[d]*phi[d];
    return -res;
}


void solve()
{
    memset(cnt, 0, sizeof(cnt));
    int L = 1, R = 0;
    LL cur = 0;
    for(int i = 1; i <= M; i++){
        while( L < Q[i].l) cur += del(a[L++]);
        while( L > Q[i].l) cur += add(a[--L]);
        while( R < Q[i].r) cur += add(a[++R]);
        while( R > Q[i].r) cur += del(a[R--]);
        ans[Q[i].idx] = cur;
        //puts("zjy");
    }
}

int main()
{
    int T_Case, Cas = 0;
    init();
    //puts("zjy");
    scanf("%d", &T_Case);
    while(T_Case--){
        scanf("%d", &N);
        for(int i = 1; i <= N; i++) scanf("%d", &a[i]);
        scanf("%d", &M);
        for(int i = 1; i <= M; i++){
            scanf("%d %d", &Q[i].l, &Q[i].r);
            Q[i].idx = i;
        }
        unit = sqrt(N);
        sort(Q+1, Q+1+M);
        solve();
        printf("Case #%d:
", ++Cas);
        for(int i = 1; i <= M; i++) printf("%lld
", ans[i]);
    }
    return 0;
}