之前一直和小伙伴探讨batch normalization层的实现机理,作用在这里不谈,知乎上有一篇paper在讲这个,链接
这里只探究其具体运算过程,我们假设在网络中间经过某些卷积操作之后的输出的feature map的尺寸为4×3×2×2
4为batch的大小,3为channel的数目,2×2为feature map的长宽
整个BN层的运算过程如下图
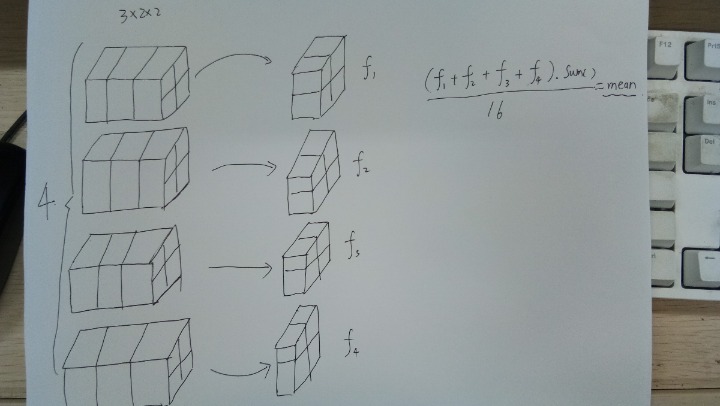
上图中,batch size一共是4, 对于每一个batch的feature map的size是3×2×2
对于所有batch中的同一个channel的元素进行求均值与方差,比如上图,对于所有的batch,都拿出来最后一个channel,一共有4×4=16个元素,
然后求区这16个元素的均值与方差(上图只求了mean,没有求方差。。。),
求取完了均值与方差之后,对于这16个元素中的每个元素进行减去求取得到的均值与方差,然后乘以gamma加上beta,公式如下

所以对于一个batch normalization层而言,求取的均值与方差是对于所有batch中的同一个channel进行求取,batch normalization中的batch体现在这个地方
batch normalization层能够学习到的参数,对于一个特定的channel而言实际上是两个参数,gamma与beta,对于total的channel而言实际上是channel数目的两倍。
用pytorch验证上述想法是否准确,用上述方法求取均值,以及用batch normalization层输出的均值,看看是否一样
上代码
1 # -*-coding:utf-8-*- 2 from torch import nn 3 import torch 4 5 m = nn.BatchNorm2d(3) # bn设置的参数实际上是channel的参数 6 input = torch.randn(4, 3, 2, 2) 7 output = m(input) 8 # print(output) 9 a = (input[0, 0, :, :]+input[1, 0, :, :]+input[2, 0, :, :]+input[3, 0, :, :]).sum()/16 10 b = (input[0, 1, :, :]+input[1, 1, :, :]+input[2, 1, :, :]+input[3, 1, :, :]).sum()/16 11 c = (input[0, 2, :, :]+input[1, 2, :, :]+input[2, 2, :, :]+input[3, 2, :, :]).sum()/16 12 print('The mean value of the first channel is %f' % a.data) 13 print('The mean value of the first channel is %f' % b.data) 14 print('The mean value of the first channel is %f' % c.data) 15 print('The output mean value of the BN layer is %f, %f, %f' % (m.running_mean.data[0],m.running_mean.data[0],m.running_mean.data[0])) 16 print(m)
用
m = nn.BatchNorm2d(3)
声明新的batch normalization层,用
input = torch.randn(4, 3, 2, 2)
模拟feature map的尺寸
输出值

咦,怎么不一样,貌似差了一个小数点,可能与BN层的momentum变量有关系,在生命batch normalization层的时候将momentum设置为1试一试
m.momentum=1
输出结果

没毛病
至于方差以及输出值,大抵也是这样进行计算的吧,留个坑