B. Recursive Queries
time limit per test
2 secondsmemory limit per test
256 megabytesinput
standard inputoutput
standard outputLet us define two functions f and g on positive integer numbers.
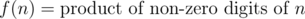

You need to process Q queries. In each query, you will be given three integers l, r and k. You need to print the number of integers xbetween l and r inclusive, such that g(x) = k.
Input
The first line of the input contains an integer Q (1 ≤ Q ≤ 2 × 105) representing the number of queries.
Q lines follow, each of which contains 3 integers l, r and k (1 ≤ l ≤ r ≤ 106, 1 ≤ k ≤ 9).
Output
For each query, print a single line containing the answer for that query.
Examples
input
Copy
4
22 73 9
45 64 6
47 55 7
2 62 4
output
1
4
0
8
input
Copy
4
82 94 6
56 67 4
28 59 9
39 74 4
output
3
1
1
5
Note
In the first example:
- g(33) = 9 as g(33) = g(3 × 3) = g(9) = 9
- g(47) = g(48) = g(60) = g(61) = 6
- There are no such integers between 47 and 55.
- g(4) = g(14) = g(22) = g(27) = g(39) = g(40) = g(41) = g(58) = 4
题意主要就是,g(x)等于各个数位和的乘积(不包含0),给出a,b,c,问ab之间有多少个g[x]=c。这个题目第一反应就是打表,做一个映射,然后再求前缀和。注意数组开大一点,不然会RE。还有一个坑点就是减的时候注意是开区间,所以后一个前缀和是a-1。

#include<bits/stdc++.h> using namespace std; #define maxn 2000005 int n; int num[maxn]; int cnt[maxn][10]; int deal(int n) { int sum=1; while(n) { if(n%10!=0) sum*=(n%10); n/=10; } return sum; } void create() { for(int i=1; i<=maxn; i++) { int t=deal(i); while(t>=10) t=deal(t); num[i]=t; cnt[i][t]++; } } int main() { create(); for(int i=1; i<=9; i++) for(int j=2; j<=maxn; j++) cnt[j][i]+=cnt[j-1][i]; int x,y; /*while(cin>>x>>y) cout<<cnt[x][y]<<endl;*/ scanf("%d",&n); for(int i=0; i<n; i++) { int a,b,c; scanf("%d %d %d",&a,&b,&c); int ans=cnt[b][c]-cnt[a-1][c]; //开区间注意a-1 printf("%d ",ans); } return 0; }
