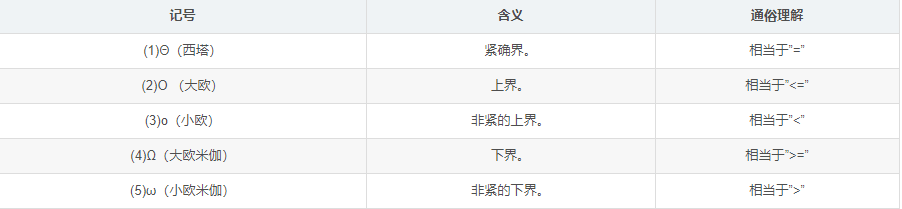
渐近符号
基本的渐近符号:
O 表示上界,即小于等于 ≤
o 表示小于 <
Ω 表示下界,即大于等于 ≥ (与O相反)
ω 表示大于 > (与o相反)
Θ 表示渐近等于 =
O( f(n) ) : 给出了算法运行时间的上界 , 也就是最坏情况下的时间复杂度
Ω( f(n) ) : 给出了算法运行时间的下界 , 也就是最好情况下的时间复杂度
θ ( f(n) ) : 给出了算法运行时间的上界和下界 , 这里 θ ( f(n) ) 是渐进的确界
渐近符号O (大)
定义 :对于f(n) = O(g(n)),表示存在适当的常数 C > 0,no>0,使得 f(n) ≤ C·g(n),对于所有的n≥no 有 f(n)≤cg(n) 。
称为 f(n) 的阶小于 g(n) 的阶。
可以理解为:
f(n)是属于g(n)构成的函数集,可以定义O(g(n))为一个函数集 O(g(n)) = { f(n):存在c>0、n0>0,使得0≤f(n)≤cg(n),其中n ≥ no }
渐近符号o (小)
定义: f(n)=o(g(n)),当且仅当f(n)=O(g(n)) 且f(n)!=Ω(g(n))。
渐近符号Θ
Θg(n) = Og(n)∩ Ωg(n) 。
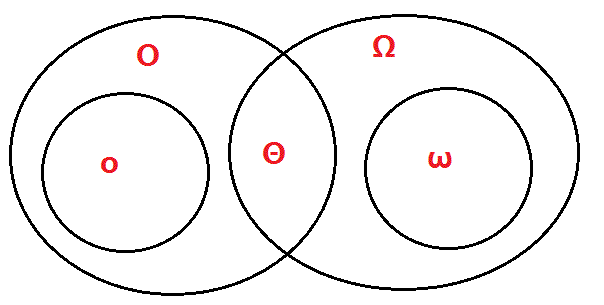
对于 渐近符号O (大)
1.线性函数
f(n)=3n+2,当n>=2时,3n+2<=3n+n=4n。
所以f(n)=O(n),这里c = 4,n0 = 2,g(n) = n, 那么cg(n) 也就是4n 就是f(n) 的上界
2.平方函数
f(n)=2n^2+3n+3,当n>=3时,3n+3<=4n,当n>=4时,4n<n^2,f(n)=2n^2+n^2=3n^2。
f(n)=O(n^2),这里c = 3,n0 = 4, g(n) = n^2 ,那么cg(n) 也就是3n^2 就是f(n) 的上界
3.指数函数
f(n)=6*2^n+n^2,当n>=4时,n^2<=2^n,所以当n>=4,有f(n)<=6*2^n+2^n=7*2^n。
这里c是7,n0=4,f(n)=O(2^n)。
4.常数阶
f(n)=9,这里就直接记为O(1),c为9,n0为0就可以了,f(n)=9<=9*1。