2.1二分类
(1)以一张三通道的64×64的图片做二分类识别是否是毛,输出y为1时认为是猫,为0时认为不是猫:

y输出是一个数,x输入是64*64*3=12288的向量。
(2)以下是一些符号定义(数据集变成矩阵之后进行矩阵运算代替循环运算,更加高效)
x:表示一个nx维数据,维度为(nx,1)
y:表示输出结果,取值为(0,1);
(x(i),y(i)):表示第i组数据;
X=[x(1),x(2),……,x(m)]:表示按列将所有的训练数据集的输入值堆叠成一个矩阵;其中m表示样本数目;
Y=[y(1),y(2),……,y(m)]:表示所有输入数据集对于的输出值,其维度为1×m;
2.2逻辑回归
(1)逻辑回归的输出值是一个概率,算法思想如下:
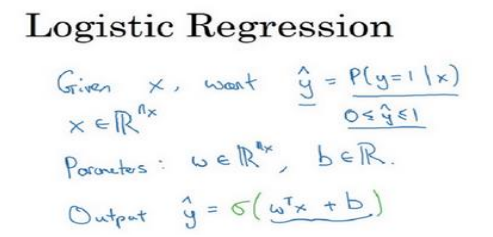
(2)激活函数使用sigmoid,它使得输出值限定在0到1之间,符合概率的取值。
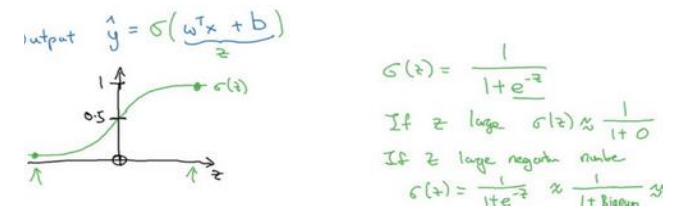
(3)关于偏置项(偏差)b,可将其变成θ0,对应的x0恒定为1,如下所示:
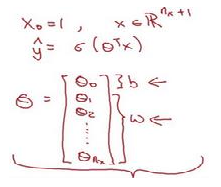
2.3逻辑回归的代价函数
(1)损失函数(针对单个样本):
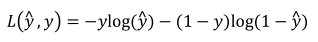
(2)代价函数(针对全部训练样本):
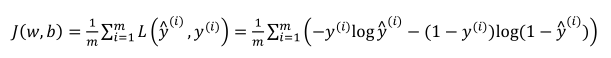
2.4梯度下降法
(1)下图中左边为凸函数,右边为非凸函数,逻辑回归中代价函数为凸函数,故任意的初始化都能收敛到最优点:


(2)参数w、b的更新方式:
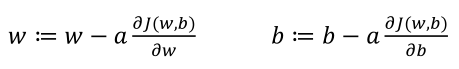
2.5导数
导数即斜率。
2.6跟多的导数例子
记住一些常见的导数求法或者直接查看导数表。
2.7计算图
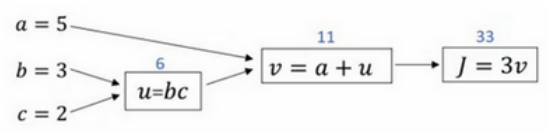
(1)下图展示计算图计算的过程:
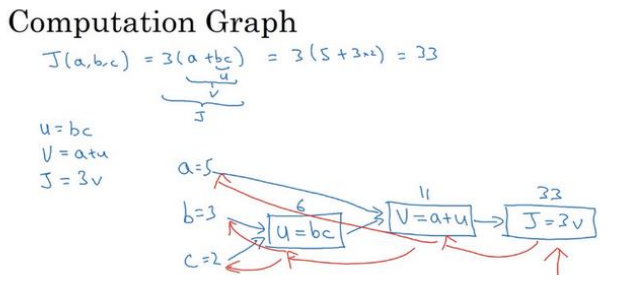
(2)正向传播用于计算代价函数
2.8计算图的导数计算
(1)反向传播利用链式法则来进行求导,如对a进行求导,其链式法则公式为:
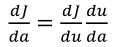
2.9逻辑回归中的梯度下降
针对于单个样本
(1)计算图如下:

(2)首先计算da:
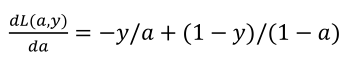
(3)然后计算dz:
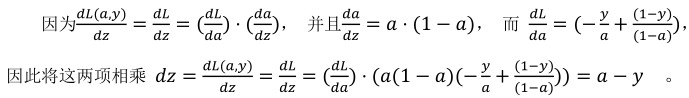
(4)最后计算dw,db(下面的式子其实已经对所有样本进行的求导):
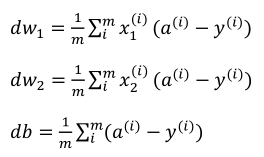
2.10m个样本的梯度下降法
(1)以下代码显示了对整个数据集的一次迭代


(2)以上过程会有两个循环,一个循环是循环是遍历样本,第二个循环是当w很多时是要循环的,上面之写出了两个w,所以没体现出来。
2.11向量化
(1)使用循环的方式计算:ωTx

(2)使用向量的方式

后者不仅书写简单,更重要的是计算速度可以比前者快特别多。
2.12向量化的更多例子
(1)消除w带来的循环
设置u=np.zeros(n(x),1)来定义一个x行的一维向量,从而替代循环,仅仅使用一个向量操作dw=dw+x(i)dz(i),最后我们得到dw/m。
2.13向量化逻辑回归
(1)将样本x横向堆叠,形成X,同时根据python的广播性质(把实数b变成了(1,m)维),得到:

(2)继续利用Python的计算方法,得到A:
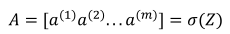
2.14向量化logistic回归的梯度输出
(1)没有用向量化时使用的代码:

(2)使用向量化之后的代码:
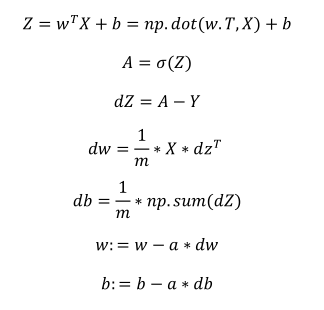
其中前面五个式子完成了前向和后向的传播,也实现了对所有训练样本进行预测和求导,再利用后两个式子,梯度下降更新参数。另外如果需要多次迭代的话,还是需要用到一个循环的,那是避免不了的。
2.15Python中的广播
(1)下图形象的总结了Python中的广播
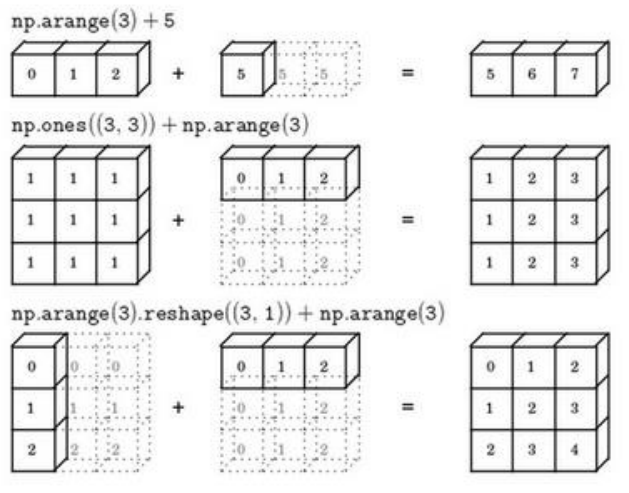
(2)在Python的numpy中,axis=0是按照列操作,axis=1,是按照行操作,这一点需要注意。
2.16关于python_numpy向量的说明
(1)使用a=np.random.randn(5)生成的数据结构在python中称为一维数组,它既不是行向量也不是列向量,用a.shape的结果是(5,)这表示它是一个一维向量,a和它的转置相乘其实得到的是一个数。
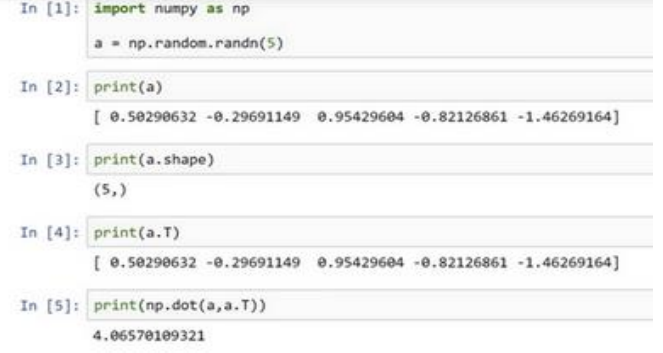
(2)应该使用a=np.random.randn(5,1)这样生成的是一个行向量,它和他的转置乘积会是一个矩阵:

2.17Jupyter/iPython Notebooks快速入门
2.18(选修)logistics损失函数的解释
(1)首先需要明确,逻辑回归的输出表示y等于1的概率。故有:
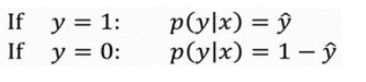
(2)合并成一个式子(要使得式子越大越好):
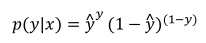
(3)根据对数函数log的单调递增性,对上式取对数有:
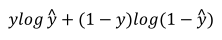
(4)要最大化上式,最小化上式取反,得到一个样本的损失函数。
(5)所有样本时,认为样本间独立同分布,故联合概率就是每个样本的乘积:

(6)两边取对数得到:
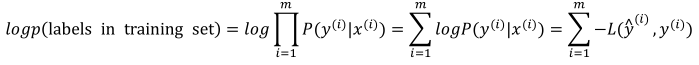
(7)要最大化上式(最大似然估计)也就是最小化:
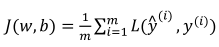
总结一下:为了最小化成本函数J(w,b),我们logistic回归模型的最大似然估计的角度出发,假设训练集中的样本都是独立同分布的条件下。