多因素线性回归|adjusted R^2|膨胀系数|非线性回归|Second-order model with 1 independent variable|Interaction model with 2 independent variables|偏相关|fraction[a]|contribution

多因素线性回归

 

系数由最小二乘法得到

 

 

 R^2;adjusted R^2:变量变多之后，r^2自然变大，但是这不是反应客观事实，所以引入了adjusted R^2

 

使用散点图看独立性，也可以使用软件，car package：

 

任何一个变量显著便使得整个模型（y）显著。

要保证各变量之间相互独立，否则一个变量改变之后另一个变量改变，这两个变量都改变之后y必然改变，但是实际上是第一个变量导致的。所以要检查多元共线性，可使用膨胀系数，相关系数仅考查两个变量之间的关系，而膨胀系数考查一个变量与其他所有变量之间的关系。

 

当变量之间存在相关性，就要变量选择

非线性回归：

由非常规数据转换后变成正比例函数，但也可以不改变：eg朱鹮

 

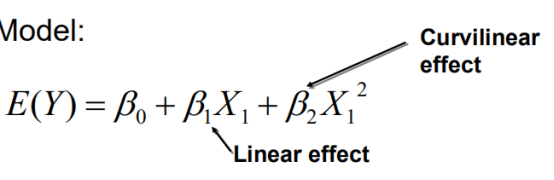
Second-order model with 1 independent variable，即同一个item不同的变量，比如都是x1：

Interaction model with 2 independent variables

 

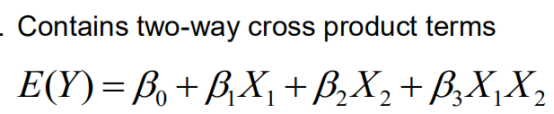
综合以上线性项，高次项及交互项，将它们相互搭配：

 

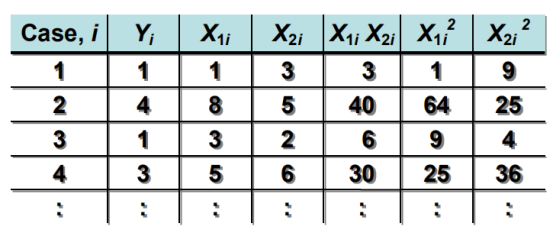
最好使用backward方法，即将所有可能放入模型，比如高次项或高次项，如果没有则会扔掉。二次通常都保留了，但是三次项不考虑。二阶交互项考虑，三次交互项不考虑。因为三次构图比较复杂。

 

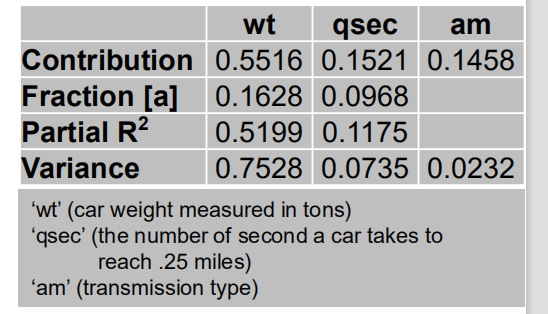
多元相关是预测值与观测值（多种观测值）之间的关系。

con是x2保持不变，另一个变量x1和y之间的关系。

 

 

Contribution为贡献度，可视为百分比。

Fraction在保证其他变量不变的情况下的r^2,它与偏相关的区别是，fraction认为其他变量为常量，而偏相关系数是研究所有变量中某一种变量与y之间的关系。