(A)
曲明连sb模拟不会做,拖出去埋了算了
//quming
#include<bits/stdc++.h>
#define R register
#define fi first
#define se second
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
typedef pair<int,int> pi;
const int N=2005;
char s[N];int n,k,top,T;pi st[N];
void find(int pos,int c){
if(s[pos]==c)return;
fp(i,pos+1,n)if(s[i]==c){
st[++top]=pi(pos,i),reverse(s+pos,s+i+1);
return;
}
}
int main(){
for(scanf("%d",&T);T;--T){
scanf("%d%d",&n,&k),top=0,--k;
scanf("%s",s+1);
fp(i,1,k<<1)find(i,(i&1)?'(':')');
R int sz=n-(k<<1);
fp(i,1,sz)find(i+(k<<1),i<=sz?'(':')');
printf("%d
",top);
fp(i,1,top)printf("%d %d
",st[i].fi,st[i].se);
}
return 0;
}
(B)
离线之后sort一下依次加入每个元素,每次查询(k)大值就行了,我抄了个平衡树板子,实际上二分+树状数组就行了
//quming
#include<bits/stdc++.h>
#define R register
#define pb push_back
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
unsigned int aaa=19260817;
inline unsigned int rd(){aaa^=aaa>>15,aaa+=aaa<<12,aaa^=aaa>>3;return aaa;}
const int N=2e5+5;
struct node;typedef node* ptr;
struct node{
ptr lc,rc;int v,sz;unsigned int pr;
inline void init(R int val){v=val,pr=rd(),sz=1;}
inline ptr upd(){return sz=lc->sz+rc->sz+1,this;}
}e[N],*rt=e;int tot;
inline ptr newnode(R int v){return e[++tot].init(v),(e+tot)->lc=(e+tot)->rc=e,e+tot;}
void split(ptr p,int k,ptr &s,ptr &t){
if(p==e)return s=t=e,void();
if(p->v<=k)s=p,split(p->rc,k,p->rc,t);
else t=p,split(p->lc,k,s,p->lc);
p->upd();
}
ptr merge(ptr s,ptr t){
if(s==e)return t;if(t==e)return s;
if(s->pr<t->pr)return s->rc=merge(s->rc,t),s->upd();
return t->lc=merge(s,t->lc),t->upd();
}
void insert(int k){
ptr s,t;
split(rt,k,s,t);
rt=merge(merge(s,newnode(k)),t);
}
void erase(int k){
ptr s,t,p;
split(rt,k,s,t),split(s,k-1,s,p),p=merge(p->lc,p->rc);
rt=merge(merge(s,p),t);
}
int rk(int k){
ptr s,t;int now;
split(rt,k-1,s,t);now=s->sz+1;
return rt=merge(s,t),now;
}
int Kth(ptr p,int k){
if(p->lc->sz==k-1)return p->v;
if(p->lc->sz>=k)return Kth(p->lc,k);
return Kth(p->rc,k-p->lc->sz-1);
}
int Pre(int k){
ptr s,t;int now;
split(rt,k-1,s,t),now=Kth(s,s->sz);
return rt=merge(s,t),now;
}
int nxt(int k){
ptr s,t;int now;
split(rt,k,s,t),now=Kth(t,1);
return rt=merge(s,t),now;
}
int a[N],id[N],ak[N],ad[N],ans[N],n,m;
vector<int>qr[N];
int main(){
scanf("%d",&n);
fp(i,1,n)scanf("%d",&a[i]),id[i]=i;
sort(id+1,id+1+n,[](const int &x,const int &y){return a[x]==a[y]?x<y:a[x]>a[y];});
scanf("%d",&m);
fp(i,1,m)scanf("%d%d",&ak[i],&ad[i]),qr[ak[i]].pb(i);
fp(i,1,n){
insert(id[i]);
for(auto v:qr[i])ans[v]=Kth(rt,ad[v]);
}
fp(i,1,m)printf("%d
",a[ans[i]]);
return 0;
}
(C)
曲明连sb二分都不会做,可以拖出去埋了
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int N=1e6+5;
char s[N];
vector<int>sm[N],a[N],d[N],g[N];
int n,m,cnt,h,t,l,r,mid,ans;
inline void init(){
fp(i,0,n+1){
sm[i].resize(m+2),
a[i].resize(m+2),
d[i].resize(m+2),
g[i].resize(m+2);
}
}
inline int calc(R int x,R int y,R int xx,R int yy){
return sm[xx][yy]+sm[x-1][y-1]-sm[x-1][yy]-sm[xx][y-1];
}
inline bool ok(R int i,R int j,R int mid){
return calc(i-mid,j-mid,i+mid,j+mid)==(mid<<1|1)*(mid<<1|1);
}
bool ck(){
fp(i,0,n+1)fp(j,0,m+1)g[i][j]=0;
fp(i,mid+1,n-mid)fp(j,mid+1,m-mid)
if(ok(i,j,mid)){
++g[i-mid][j-mid],++g[i+mid+1][j+mid+1];
--g[i-mid][j+mid+1],--g[i+mid+1][j-mid];
}
R int fl=1;
fp(i,1,n)fp(j,1,m){
g[i][j]+=g[i-1][j]+g[i][j-1]-g[i-1][j-1];
if((g[i][j]>0)!=a[i][j])fl=0;
}
return fl;
}
int main(){
// freopen("testdata.in","r",stdin);
scanf("%d%d",&n,&m);init();
fp(i,1,n){
scanf("%s",s+1);
fp(j,1,m){
a[i][j]=(s[j]=='X');
sm[i][j]=sm[i-1][j]+sm[i][j-1]-sm[i-1][j-1]+a[i][j];
}
}
l=0,r=min(n+1,m+1)>>1,ans=0;
while(l<=r){
mid=(l+r)>>1;
ck()?(ans=mid,l=mid+1):r=mid-1;
}
printf("%d
",ans);
fp(i,1,n)fp(j,1,m)d[i][j]=0;
fp(i,ans+1,n-ans)fp(j,ans+1,m-ans)d[i][j]=ok(i,j,ans);
fp(i,1,n){
fp(j,1,m)putchar(d[i][j]?'X':'.');
putchar('
');
}
return 0;
}
(D)
记一个(c),考虑每个(i),如果(a_i=h_i)令(--c),如果(a_i=h_{i+1})令(++c),相当于求最终(c>0)的方案,那么根据(h_i)和(h_{i+1})是否相等判断一下(a_i)对(c)的贡献写出生成函数,手动多项式快速幂就行了
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int P=998244353;
inline void upd(R int &x,R int y){(x+=y)>=P?x-=P:0;}
inline int inc(R int x,R int y){return x+y>=P?x+y-P:x+y;}
inline int dec(R int x,R int y){return x-y<0?x-y+P:x-y;}
inline int mul(R int x,R int y){return 1ll*x*y-1ll*x*y/P*P;}
int ksm(R int x,R int y){
R int res=1;
for(;y;y>>=1,x=mul(x,x))(y&1)?res=mul(res,x):0;
return res;
}
const int N=(1<<19)+5;
int rt[2][N],r[21][N],inv[21],lg[N],lim,d;
void init(){
fp(d,1,19){
fp(i,1,(1<<d)-1)r[d][i]=(r[d][i>>1]>>1)|((i&1)<<(d-1));
inv[d]=ksm(1<<d,P-2),lg[1<<d]=d;
}
for(R int t=(P-1)>>1,i=1,x,y;i<524288;t>>=1,i<<=1){
x=ksm(3,t),y=ksm(332748118,t),rt[0][i]=rt[1][i]=1;
fp(k,1,i-1){
rt[0][i+k]=mul(rt[0][i+k-1],x);
rt[1][i+k]=mul(rt[1][i+k-1],y);
}
}
}
void NTT(int *A,int ty){
int t;
fp(i,0,lim-1)if(i<r[d][i])swap(A[i],A[r[d][i]]);
for(R int mid=1;mid<lim;mid<<=1)
for(R int j=0;j<lim;j+=(mid<<1))
fp(k,0,mid-1){
A[j+k+mid]=inc(A[j+k],P-(t=mul(A[j+k+mid],rt[ty][mid+k])));
upd(A[j+k],t);
}
if(!ty){
t=inv[d];
fp(i,0,lim-1)A[i]=mul(A[i],t);
}
}
int A[N],a[N];
int n,k,res,coef,cnt;
int main(){
// freopen("testdata.in","r",stdin);
init();
scanf("%d%d",&n,&k);
fp(i,1,n)scanf("%d",&a[i]);
a[n+1]=a[1];
fp(i,1,n)++(a[i]==a[i+1]?coef:cnt);
if(coef==n)return puts("0"),0;
coef=ksm(k%P,coef);
A[0]=A[2]=1,A[1]=(k-2)%P;
lim=1,d=0;while(lim<=(cnt<<1))lim<<=1,++d;
NTT(A,1);
fp(i,0,lim-1)A[i]=ksm(A[i],cnt);
NTT(A,0);
fp(i,cnt+1,(cnt<<1))upd(res,A[i]);
printf("%d
",mul(res,coef));
return 0;
}
(E)
首先默认(a_ileq a_{i+1}),并且默认(a_ileq n-1)
这样的话我们就可以有一种放法,对于一个(n imes n)的网格,强制副对角线上所有格子不能放元素,然后每一列都从这一列的副对角线格子上方开始放起,这样由于(a_ileq a_{i+1}),所以相邻两列的放了元素的格子的顶端一定不同
大概长这样,红色表示不能放,黑色表示放了的格子,(a_2=a_3=a_4=2),但它们的顶端各不相同
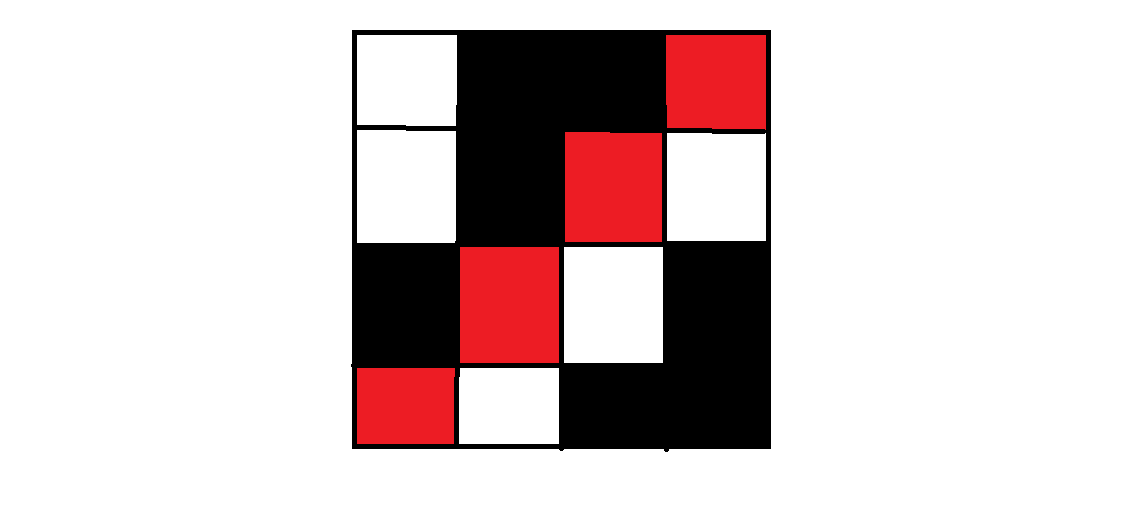
这样的话我们可以证明任意两行一定不同
如果有的元素满足(a_i=n),然后我们直接把它的第(n)个元素扔到第(n+1)行,有可能出现的一个问题就是第(n)行和第(n+1)行相等。一种解决办法就是我们找到第(n+1)行的黑格子的左边界,记为(i),由于(i)是左边界,那么第(n)行里第(i-1)个格子一定是白的,我们把第(n+1)行第(i)个格子和第(i)列副对角线上那个格子交换,容易证明这样之后依然是合法的
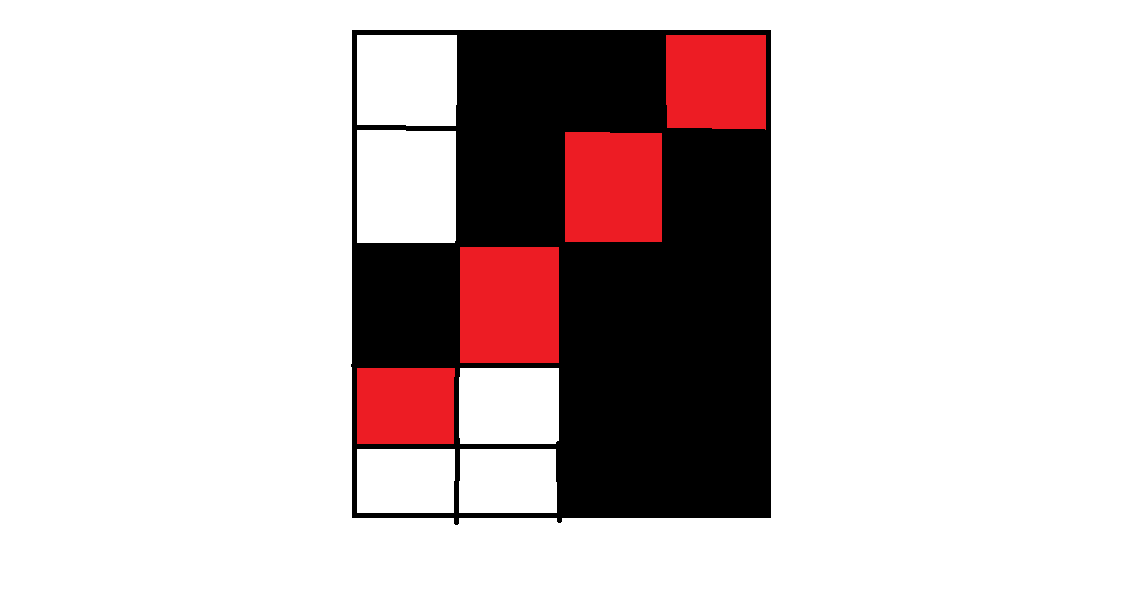
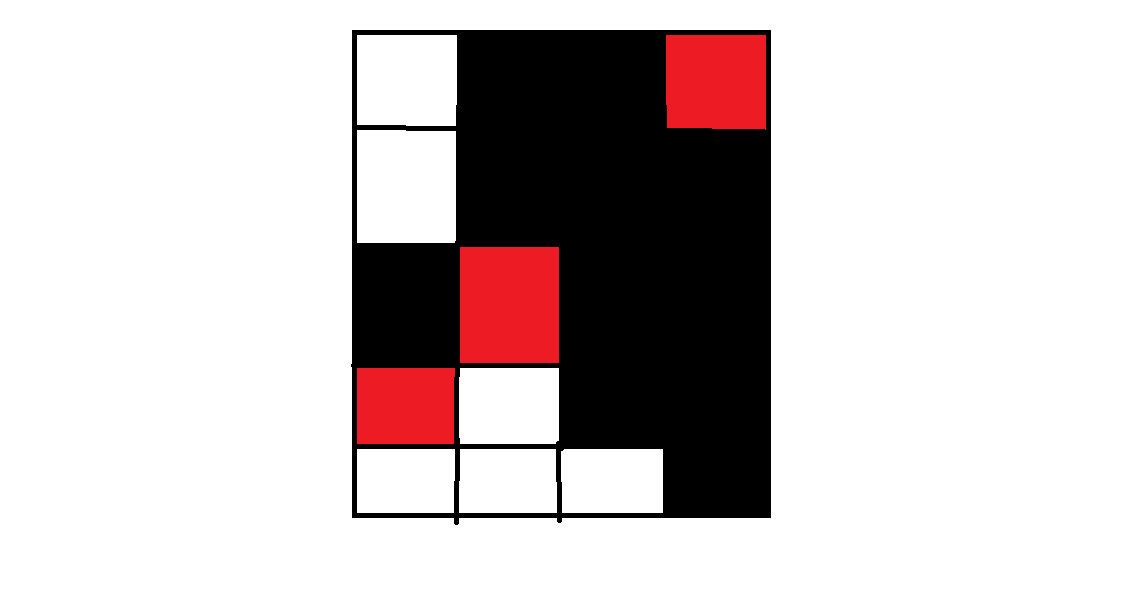
//quming
#include<bits/stdc++.h>
#define R register
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int N=1005;
int mp[N][N],a[N],id[N],n;
int main(){
// freopen("testdata.in","r",stdin);
scanf("%d",&n);
fp(i,1,n)scanf("%d",&a[i]),id[i]=i;
sort(id+1,id+1+n,[](const int &x,const int &y){return a[x]<a[y];});
fd(i,n,1)for(R int j=n-i,k=1;k<=min(n-1,a[id[i]]);++k,--j){
if(!j)j=n;
mp[j][id[i]]=1;
}
fp(i,1,n)if(a[i]==n)mp[n+1][i]=1;
R bool fl=1;
fp(i,1,n)if(mp[n][i]!=mp[n+1][i]){fl=0;break;}
if(fl){
// puts("QAQ");
fd(i,n,1)if(a[id[i]]==n&&a[id[i-1]]!=n){
mp[n+1][id[i]]=0,mp[n-i+1][id[i]]=1;
break;
}
}
printf("%d
",n+1);
fp(i,1,n+1){
fp(j,1,n)putchar(mp[i][j]+'0');
putchar('
');
}
return 0;
}
(F)
我们把所有的线段都拆成形如([x,x+2^k-1])的样子,其中(x)的二进制的(0)到(k-1)位全都为(0),对于一条原来的线段,拆掉它之后产生的所有线段其实就是(l)和(r)的trie树上的路径的所有儿子,所以我们可以证明拆完之后总线段数是(O(n imes 60))的
对于两条形如([x,x+2^k-1])和([y,y+2^g-1])的线段,假设(k<g),并设(p=xoplus y)的前(59-g)位,我们发现这两条线段可以异或出([p,p+2^g-1])之间的所有数字,而且(p)是一个固定的前缀。所以我们可以枚举所有合法的线段,而最终的贡献就相当于trie树的一个子树全部合法,打上标记就行了,最后在trie树上dfs一遍就行了,总复杂度(O(n^260^3)),卡一卡就能过
//quming
#include<bits/stdc++.h>
#define R register
#define fi first
#define se second
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;}
using namespace std;
const int P=998244353;
inline void upd(R int &x,R int y){(x+=y)>=P?x-=P:0;}
inline int inc(R int x,R int y){return x+y>=P?x+y-P:x+y;}
inline int dec(R int x,R int y){return x-y<0?x-y+P:x-y;}
inline int mul(R int x,R int y){return 1ll*x*y-1ll*x*y/P*P;}
int ksm(R int x,R int y){
R int res=1;
for(;y;y>>=1,x=mul(x,x))(y&1)?res=mul(res,x):0;
return res;
}
typedef long long ll;
typedef pair<ll,int> pi;
typedef pair<ll,ll> ppi;
const int N=200005;
int n,na,nb,top;pi sa[N],sb[N];ppi st[N];
void get(){
scanf("%d",&n);
fp(i,1,n)scanf("%lld%lld",&st[i].fi,&st[i].se);
sort(st+1,st+1+n,[](const ppi &a,const ppi &b){return a.fi<b.fi;});
top=1;
fp(i,2,n)if(st[i].fi<=st[top].se+1)cmax(st[top].se,st[i].se);
else st[++top]=st[i];
}
void build(pi *s,int &n,ll l,ll r){
for(R ll i=l,p=0;i<=r;i+=(1ll<<p)){
while((i>>p&1^1)&&(i+(1ll<<(p+1))-1)<=r)++p;
while(p&&(i+(1ll<<p)-1)>r)--p;
s[++n]=pi(i,p);
}
}
const int M=1e7+5;
int ch[M][2],vis[M],bin[233],nd,res;
void ins(R ll x,int k){
R int p=0,c;
fd(i,59,k){
c=(x>>i&1);
if(!ch[p][c])ch[p][c]=++nd;
if(vis[p=ch[p][c]])return;
}
vis[p]=1;
}
void dfs(int p,int pos,int coef){
if(vis[p]){
upd(res,mul(coef,bin[pos+1]));
upd(res,mul(bin[pos+1]-1,bin[pos]));
return;
}
if(ch[p][0])dfs(ch[p][0],pos-1,coef);
if(ch[p][1])dfs(ch[p][1],pos-1,inc(coef,bin[pos]));
}
int main(){
// freopen("testdata.in","r",stdin);
get();
fp(i,1,top)build(sa,na,st[i].fi,st[i].se);
get();
fp(i,1,top)build(sb,nb,st[i].fi,st[i].se);
bin[0]=1;fp(i,1,60)bin[i]=mul(bin[i-1],2);
sort(sa+1,sa+1+na,[](const pi &a,const pi &b){return a.se>b.se;});
sort(sb+1,sb+1+nb,[](const pi &a,const pi &b){return a.se>b.se;});
fp(i,1,na)fp(j,1,nb)ins(sa[i].fi^sb[j].fi,max(sa[i].se,sb[j].se));
dfs(0,59,0);
printf("%lld
",res);
return 0;
}