无向图: 有向图 : 子图
路径:由vi到vj 中途会经过其他几个点 如果vi=vj,则称之为回路或者环。 如果这条路径上没有相同点,则称之为简单路径,如果只有vi=vj,称之为简单回路或者简单环。
完全图:每个顶点都和其余n-1个顶点有边相连(意思是直接一步到位,这两点之间有连线),无向完全图要求Cn2=n(n-1)/2;有向完全图要求An2n(n-1); 这是图的边数的最大值;
连通图:在有向图or无向图基础上, 如果任意两个顶点之间都有路径可以到达(不一定要有连线,有中间商可以,只要最后到了就行),则称之为(无向图->)连通图/(有向图->)强连通图;
非连通图/非强连通图; n个顶点的连通图最多n(n-1)/2条边,至少n-1条边(构成一棵树); 强连通图最多n(n-1)条边,最少n条边,构成一个首尾相连的环
连通分量:无向图的极大连通子图//////子图+连通+极大 首先得是子图,其次得是连通的子图,各个点可以到达另一个点,再者是极大:将图的任何不在该子图中的顶点加进来,该子图不在连通;'/''''''注意:想加进来的这个点 也得是母图的一个顶点,just不在子图内而已//////当然试验的时候,这个顶点的边也得一起来看、///////////////////如果加进来一个新的顶点(of courser还有他的边)导致子图仍然是连通的,那么该子图就成不上是极大连通子图 即连通分量;
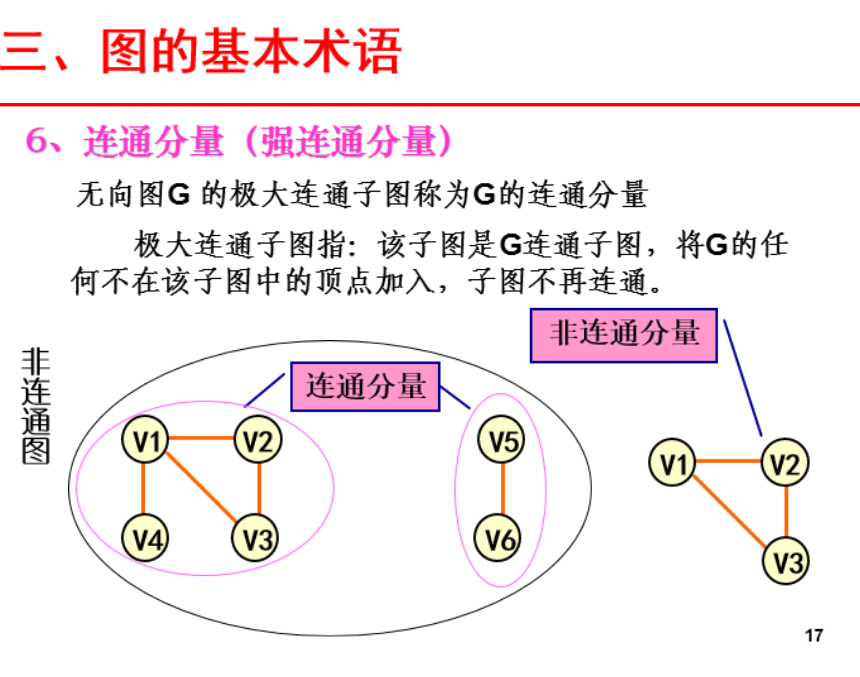
与此相对应的是: 有向图的强连通分量(有向图的极大连通子图)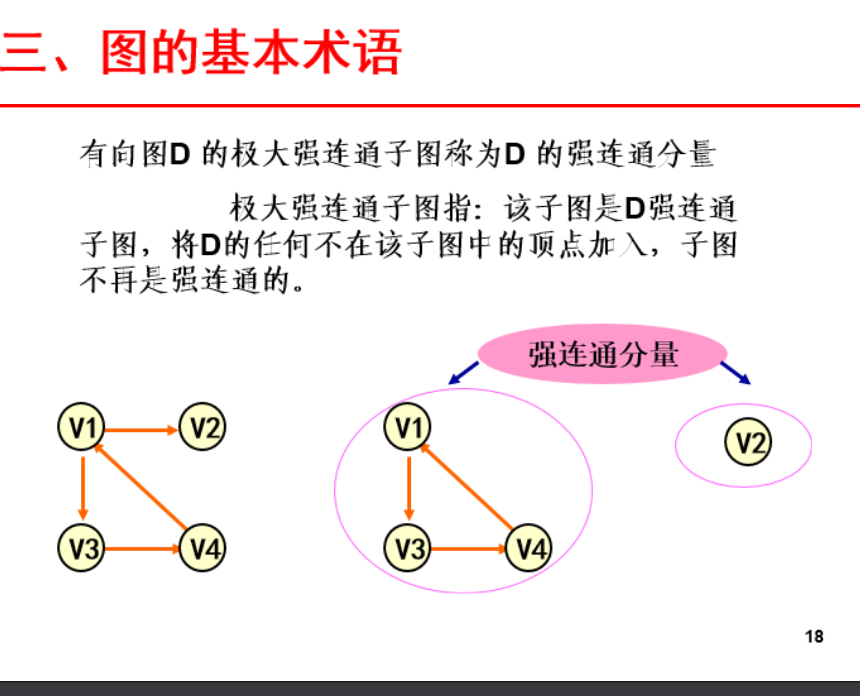
一个无向图要想连通,最少n-1条边的
生成树T:对应无向图G
仍然是图,只是 包含G 的所有顶点,的,极小连通子图(若删除任何一条边,图都不在连通)
T满足的条件:当且仅当:1.是G的连通子图 2.包含所有顶点 3.无回路
如果路径带上权值的话,那就有最小生成树的出现了