激活函数与权值初始化

1.sigmod函数——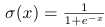（tf.nn.sigmoid()）

sigmod函数性质：

1.如图像所示其值域在[0,1]之间，函数输出不是0均值的，权重更新效率降低，因为这会导致后层的神经元的输入是非0均值的信号，这会对梯度产生影响：假设后层神经元的输入都为正(e.g. x>0 elementwise in ),那么对w求局部梯度则都为正，这样在反向传播的过程中w要么都往正方向更新，要么都往负方向更新，导致有一种捆绑的效果，使得收敛缓慢。 当然了，如果你是按batch去训练，那么每个batch可能得到不同的符号（正或负），那么相加一下这个问题还是可以缓解。因此，非0均值这个问题虽然会产生一些不好的影响，不过跟上面提到的 kill gradients 问题相比还是要好很多的。

2.如图当其取值远离原点时，其梯度越来越小趋近于0，在反向传播中，用链式求导法，求权值求梯度，梯度逐层减小，权值更新速度缓慢，一般不超过五层sigmod层，就会出现梯度弥散，即梯度饱和问题。

3.要进行指数运算，速度慢

4.定义域(0, 1) 可以表示作概率，或者用于输入的归一化，如Sigmoid交叉熵损失函数。

5.sigmoid在压缩数据幅度方面有优势，在深度网络中，在前向传播中，sigmoid可以保证数据幅度在[0,1]内，这样数据幅度稳住了，不会出现数据扩散，不会有太大的失误。

2.tanh 函数——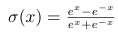(tf.nn.tanh())

　　

　

tanh函数性质

1.如图所示，值域是0均值的，权值更新快，而且也能保证数据幅度稳定。

2.也有梯度弥散问题，要进行指数运算，速度慢。

一般二分类问题中，隐藏层用tanh函数，输出层用sigmod函数

 3.relu函数——σ(x)=max(0,x)(tf.nn.relu())

relu函数性质

1.当输入为正数的时候，不存在梯度饱和问题；当输入是负数的时候，ReLU是完全不被激活的，这就表明一旦输入到了负数，ReLU就会死掉。这样在前向传播过程中，还不算什么问题，有的区域是敏感的，有的是不敏感的。但是到了反向传播过程中，输入负数，梯度就会完全到0，这个和sigmod函数、tanh函数有一样的问题。

2.ReLU函数也不是以0为中心的函数,权值更新慢

3.计算速度要快很多。ReLU函数只有线性关系，不管是前向传播还是反向传播，都比sigmod和tanh要快很多。

4.在正向传播时，relu不会对数据做幅度压缩，所以如果数据的幅度不断扩张，那么模型的层数越深，幅度的扩张也会越厉害，最终会影响模型的表现。

5.但是relu在反向传导方面可以很好地将梯度传到后面，这样在学习的过程中可以更好地发挥出来。

 

4.elu函数——(tf.nn.elu())

　　　　　　 　　　　

ELU函数是针对ReLU函数的一个改进型，相比于ReLU函数，在输入为负数的情况下，是有一定的输出的，而且这部分输出还具有一定的抗干扰能力。这样可以消除ReLU死掉的问题，不过还是有梯度饱和和指数运算的问题。

5.prelu函数——σ(x)=max(ax,x)(tf.nn.relu())

1.参数α一般是取0~1之间的数，而且一般还是比较小的，如零点零几。当α=0.01时，PReLU为Leaky ReLU。

2.PReLU也是针对ReLU的一个改进型，在负数区域内，PReLU有一个很小的斜率，虽然斜率很小，但是不会趋于0。这样也可以避免ReLU死掉的问题。相比于ELU，PReLU在负数区域内是线性运算，速度快。

6.softplus函数——σ(x)=log(1+e^x)(tf.nn.softplus())

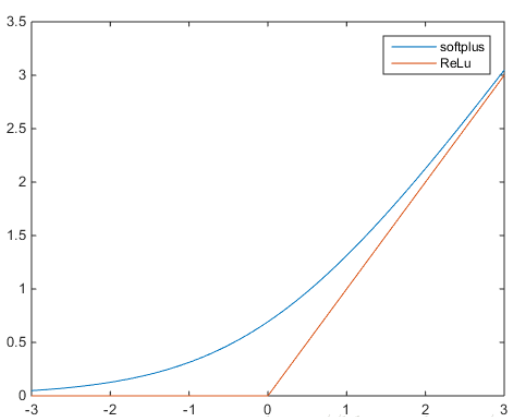
 softplus可以看作是ReLu的平滑。根据神经科学家的相关研究，softplus和ReLu与脑神经元激活频率函数有神似的地方。也就是说，相比于早期的激活函数，softplus和ReLu更加接近脑神经元的激活模型。

 

7.softmax函数

softmax把一个k维的real value向量（a1,a2,a3,a4….）映射成一个（b1,b2,b3,b4….）其中bi是一个0-1的常数，且k项之和为1，用于多分类任务，bi最大的那一项为所属类别。

8.maxout函数

 

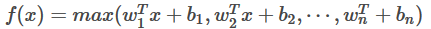
f(x)=max(wT1x+b1,wT2x+b2,⋯,wTn+bn)

是将激活函数用一层全链接层取拟合，输出为，那层的最大值，理论maxout网络能够近似任意连续函数，且当w2,b2,…,wn,bn为0时，退化为ReLU。Maxout能够缓解梯度消失，同时又规避了ReLU神经元死亡的缺点，但增加了参数和计算量，对于中间层数k，其参数会随k增长。

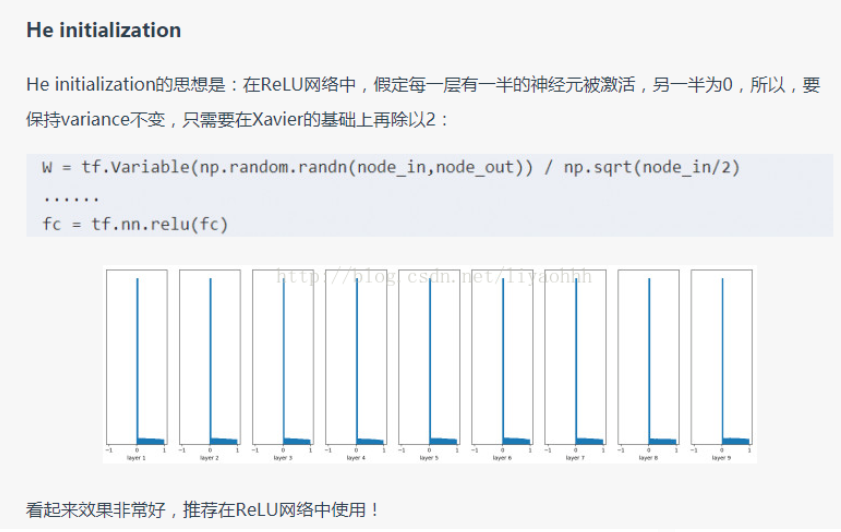
权值初始化

1.高斯初始化

2.均值初始化

3.Xavir初始化——(tf.contrib.layer.xavier_initializer_conv2d())

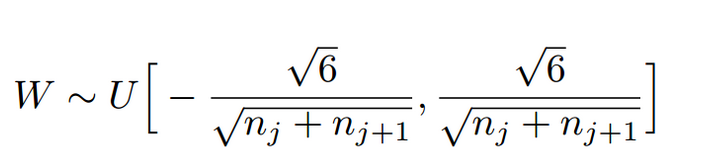
如上图nj为第j层的节点数，为均匀分布均值为1，且保证前向传播和反向传播时每一层的方差一致,原因可以见论文及其解释为了，当激活函数为sigmoid和tanh的时候比较适用。


• X. Glorot and Y. Bengio. Understanding the difficulty of training deepfeedforward neural networks. In International Conference on Artificial Intelligence and Statistics, pages 249–256, 2010.
• Y. Jia, E. Shelhamer, J. Donahue, S. Karayev, J. Long, R. Girshick, S.Guadarrama, and T. Darrell. Caffe: Convolutional architecture for fast featureembedding. arXiv:1408.5093, 2014.

这对梯度消失有好处？感觉只是保证了在前向传播中方差一致的问题，解决了前向传播中的数据稳定性保证问题，可以防止数据扩散和爆炸问题

4.he initia——激活函数为relu比较适用(tf.contrib.layers.variance_scaling_initializer())