sklearn之基于凝聚层次算法的聚类

'''
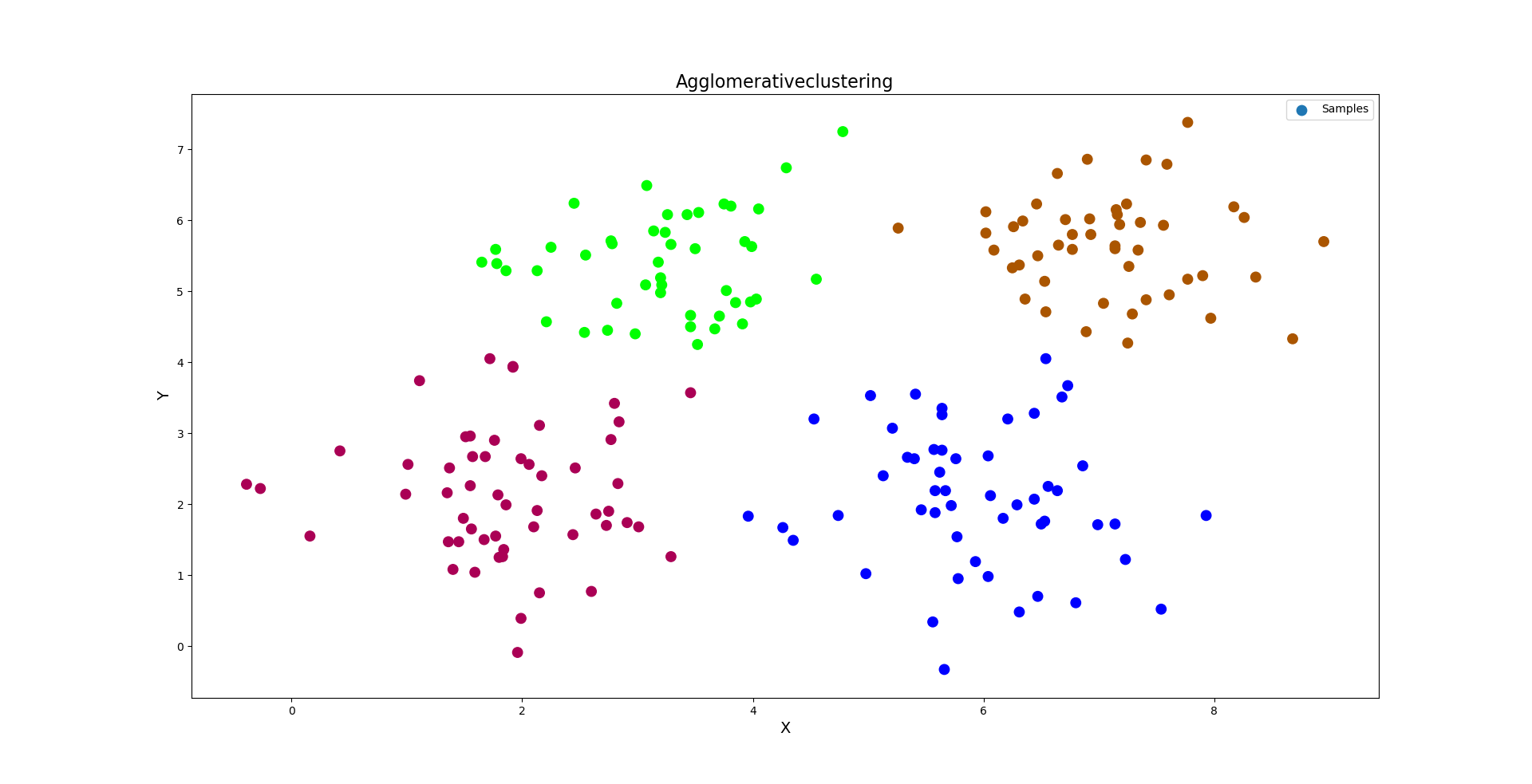
    凝聚层次算法：首先假定每个样本都是一个独立的聚类，如果统计出来的聚类数大于期望的聚类数，则从每个样本出发寻找离自己最近的另一个样本，
                与之聚集，形成更大的聚类，同时令总聚类数减少，不断重复以上过程，直到统计出来的聚类数达到期望值为止。

            凝聚层次算法的特点：
                1.聚类数k必须事先已知。借助某些评估指标，优选最好的聚类数。
                2.没有聚类中心的概念，因此只能在训练集中划分聚类，但不能对训练集以外的未知样本确定其聚类归属。不能预测。
                3.在确定被凝聚的样本时，除了以距离作为条件以外，还可以根据连续性来确定被聚集的样本。

            凝聚层次算法相关API：
                # 凝聚层次聚类器
                model = sc.AgglomerativeClustering(n_clusters=4)
                pred_y = model.fit_predict(x)   # 返回值为当前样本所属类别

    案例：重新加载multiple3.txt，使用凝聚层次算法进行聚类划分。

'''

import numpy as np
import matplotlib.pyplot as mp
import sklearn.cluster as sc

# 读取数据，绘制图像
x = np.loadtxt('./ml_data/multiple3.txt', unpack=False, dtype='f8', delimiter=',')
print(x.shape)

# 基于Agglomerativeclustering完成聚类
model = sc.AgglomerativeClustering(n_clusters=4)
pred_y = model.fit_predict(x)
print(pred_y)

# 画图显示样本数据
mp.figure('Agglomerativeclustering', facecolor='lightgray')
mp.title('Agglomerativeclustering', fontsize=16)
mp.xlabel('X', fontsize=14)
mp.ylabel('Y', fontsize=14)
mp.tick_params(labelsize=10)
mp.scatter(x[:, 0], x[:, 1], s=80, c=pred_y, cmap='brg', label='Samples')
mp.legend()
mp.show()


输出结果：

(200, 2)
[1 1 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1
 3 0 2 1 3 0 2 1 3 0 2 1 3 0 0 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 1
 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 0 3 0 2 1 3 0 2 1 3 0 2 1 3 0
 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1 1 0 2
 1 1 0 2 1 3 0 2 1 3 0 3 1 3 0 2 1 3 0 2 1 1 0 2 1 3 0 2 1 3 0 2 1 3 0 2 1
 3 0 2 1 3 0 2 1 3 0 2 1 3 0 2]