量化技术
量化的概念
一般是高精度浮点数表示的网络权值以及激活值用低精度(例如8比特定点)来近似表示
达到模型轻量化,加速深度学习模型推理,目前8比特推理已经比较成熟
使用低精度的模型推理的优点:
①模型存储主要是每个层的权值,量化后模型占用空间小,32比特可以缩减至8比特
并且激活值用8比特后,减小了内存的访问带宽需求
②单位时间内处理定点运算指令比浮点数运算指令多
量化的分类
一般按照量化阶段不同分为后量化和训练时量化,用的比较多的是后量化,像tensorRT和RKNN
按照量化映射方法又可以分为对称量化和非对称量化
对称量化(int8 -128-127)
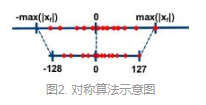

对称算法是通过一个收缩因子,将FP32中的最大绝对值映射到8比特的最大值,最大绝对值的负值(注意此值不是fp32的最小值,是最大绝对值的相反数,故对称)映射到
8比特的最小值,有对应的映射公式(较复杂,不做展示)如图所示。一般不采用zero-point。
收缩因子:![]()
对于fp32的值若均匀分布在0左右,映射后的值也会均匀分布,若fp32的值分布不均匀,映射后不能充分利用
映射空间。
非对称量化(uint8 0-255)
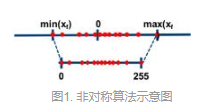

通过收缩因子和零点(用于偏移),将 FP32 张量 的 min/max 映射分别映射到 8-bit 数据的 min/max ,有对应的映射公式(较复杂,不做展示)
收缩因子: ![]()
加入零点的原因,0有特殊意义如padding,若不加零点z,量化后会映射到0,加入零点z后,浮点0量化后映射到0-255中间的一个数字。
可以无误差地量化浮点数中的数据 0,从而减少补零操作(比如卷积中的padding zero)在量化中产生额外的误差。
缺点是只有正数,有的处理方式是把0点左移到-128,范围控制在【-128,127】中,但还是非对称量化。
对称与非对称的优缺点:
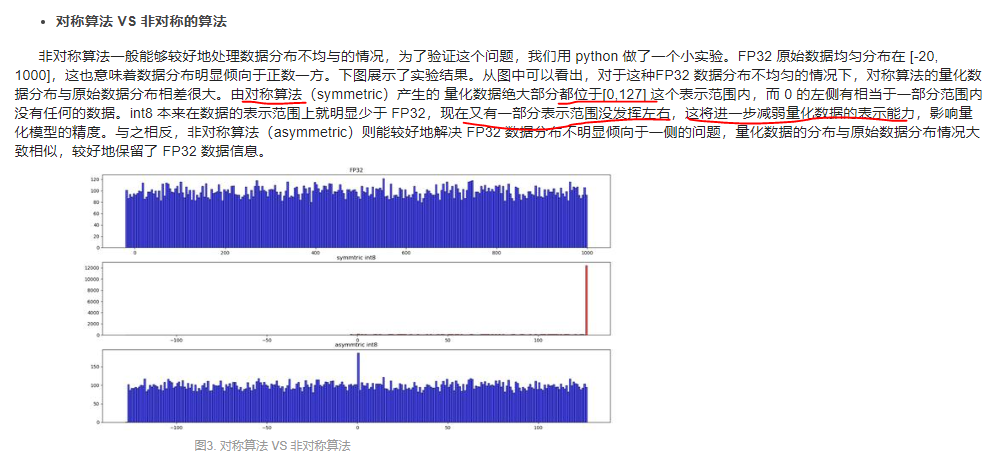
非对称可以处理好FP32数据分布不均匀的情况。
若对称算法产生的量化后数据很多都是在【0,127】内,左边的范围利用很少,减弱了量化数据的表示能力,影响模型精度。
量化的粒度
一般分为通道级量化和张量级量化,(不具体介绍概念)
通常张量的每一个通道代表一类特征,因此不同通道之间可能有数据分布相差较大情况,此时适合使用通道级量化
一般而言卷积中建议对权值使用非对称通道级的量化,激活采用张量级量化
TensorRT后量化算法
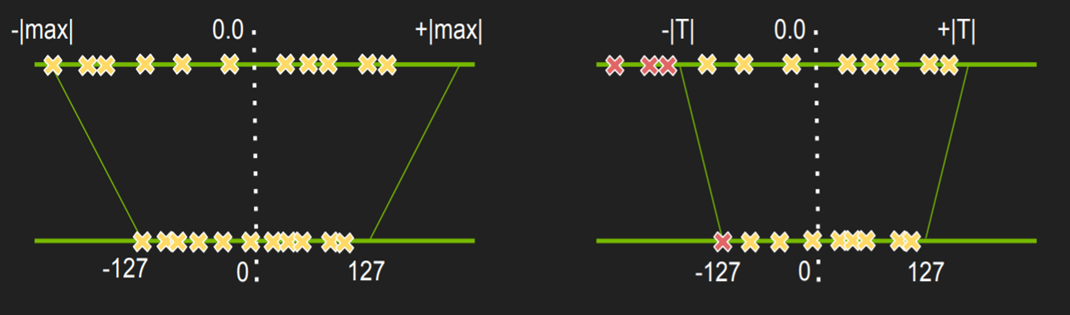
不饱和的线性量化就是量化后的数据扎堆在某一个范围(导致本不该相同的变为相同的),存在一些范围利用少的情况,会导致精度损失较大。
TensorRT量化方法:
激活值饱和量化(右图),选择合适的阈值T
权值非饱和量化(左图)
TensorRT另一个主要的优化是在层间融合或张量融合
模型推理的时候,每一次的操作都是由gpu启动不同的cuda核心来完成的,大量的时间花在cuda核心启动和读写操作上,造成了内存带宽的瓶颈和GPU资源浪费。TENSORRT通过层间融合,横向融合把卷积偏置激活合并成一个结构,并且只占用一个cuda核心,纵向融合把结构相同,权值不同的层合并成一个更宽的层,也是占用一个cuda核心,因此整个模型结构更小更快。
参考:
https://www.cnblogs.com/qccz123456/p/11767858.html
公众号 gaintpanda
rknn开发社区资料,文档