题目描述
给定一张(n)个点(m)条边的无向图。每个顶点有一个颜色,要么是黑,要么是白。我们想进行一些操作,使得最终每一条边的两个端点都是不同的颜色。每一次操作,你可以将一条边的两个端点交换颜色。求最少的操作次数和具体的操作方式。
(nleq 500)
题解
首先黑白染色,假设要让染出来的黑点最终成为黑点,那么
1.对于原来的每个黑点(i),连边((S,i,1,0))
2.对于染出来的每个黑点(i),连边((i,T,1,0))
3.对于原图中的每条边((u,v)),连边((u,v,infty,1),(v,u,infty,1)),表示交换两个端点的花费。
跑完费用流后,每次bfs找到一条从(S)到(T)的路径,通过某些方法交换第一个点和最后一个点。
对于一条长度大于(1)的路径,第一个点一定是白色的,最后一个点一定是黑色的。(第一个点靠(T),最后一个点靠(S))
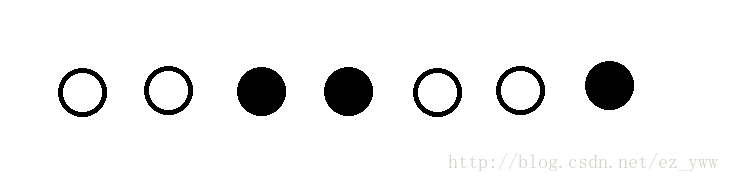
先把这个序列切成很多段,每段只有最右边的点是黑色的。

把每段的黑点调到最前面
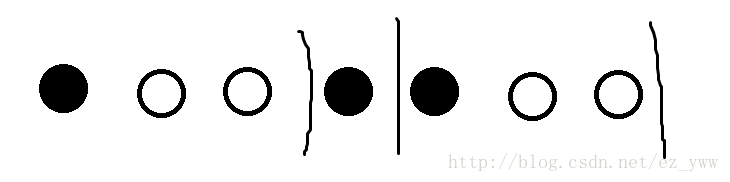
再从后往前交换每段的第一个点和前一段的最后一个点。
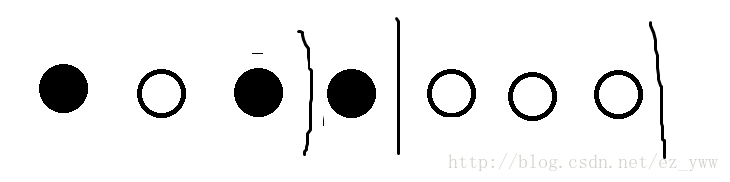
这样可以用长度(-1)步内交换第一个点和最后一个点。
时间复杂度:(O(???))
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<ctime>
#include<utility>
#include<queue>
#include<list>
#include<vector>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
queue<int> q;
//vector<pii> a;
int ax[1000010];
int ay[1000010];
int len=0;
struct li
{
int h[510];
int v[100010];
int t[100010];
int n;
li()
{
memset(h,0,sizeof h);
n=0;
}
void add(int x,int y)
{
n++;
v[n]=y;
t[n]=h[x];
h[x]=n;
}
};
li l;
struct graph
{
int h[510];
int u[500010];
int v[500010];
int w[500010];
int c[500010];
int t[500010];
int p[500010];
int n;
void clear()
{
n=0;
memset(h,0,sizeof h);
}
void add(int x,int y,int z,int d)
{
n++;
u[n]=x;
v[n]=y;
w[n]=d;
c[n]=z;
p[n]=0;
t[n]=h[x];
h[x]=n;
}
int S,T;
int gd[510];
int gb[510];
int gf[510];
int flow,cost;
int f[510];
int op(int x)
{
return ((x-1)^1)+1;
}
int spfa()
{
memset(gd,0x7f,sizeof gd);
gd[S]=0;
gf[S]=0;
q.push(S);
int i,x;
while(!q.empty())
{
x=q.front();
q.pop();
gb[x]=0;
if(gd[x]>=gd[T])
continue;
for(i=h[x];i;i=t[i])
if(c[i]&&gd[v[i]]>gd[x]+w[i])
{
gd[v[i]]=gd[x]+w[i];
gf[v[i]]=i;
if(!gb[v[i]])
{
gb[v[i]]=1;
q.push(v[i]);
}
}
}
if(gd[T]==0x7f7f7f7f)
return 0;
flow++;
cost+=gd[T];
for(i=gf[T];i;i=gf[u[i]])
{
c[i]--;
p[i]++;
c[op(i)]++;
p[op(i)]--;
}
return 1;
}
int maxflow()
{
flow=cost=0;
while(spfa());
return cost;
}
int p1[500010];
int p2[500010];
void check()
{
memset(gb,0,sizeof gb);
gb[S]=1;
gf[S]=0;
q.push(S);
int i;
while(!q.empty())
{
int x=q.front();
q.pop();
for(i=h[x];i;i=t[i])
if(p[i]&&!gb[v[i]])
{
gb[v[i]]=1;
gf[v[i]]=i;
if(v[i]==T)
{
while(!q.empty())
q.pop();
return;
}
q.push(v[i]);
}
}
}
void getans()
{
check();
int i;
int t1=0,t2=0;
for(i=gf[T];i;i=gf[u[i]])
{
if(v[i]!=T)
p1[++t1]=v[i];
p[i]--;
}
for(i=t1;i>=2;i--)
if(f[p1[i-1]])
p2[++t2]=i;
else
{
// a.push_back(pii(p1[i-1],p1[i]));
ax[++len]=p1[i-1];
ay[len]=p1[i];
swap(f[p1[i]],f[p1[i-1]]);
}
for(i=t2;i>=1;i--)
{
// a.push_back(pii(p1[p2[i]],p1[p2[i]-1]));
ax[++len]=p1[p2[i]];
ay[len]=p1[p2[i]-1];
swap(f[p1[p2[i]]],f[p1[p2[i]-1]]);
}
}
};
graph g1,g2;
char s[510];
int c[510];
int from[510][510];
int d[510][510];
int vis[100010];
int s1,s2;
int b,w;
int ans;
list<int> e,e1,e2;
void failed()
{
printf("-1
");
exit(0);
}
void dfs(int x,int p)
{
if(~vis[x])
{
if(vis[x]!=p)
failed();
return;
}
e.push_back(x);
vis[x]=p;
if(c[x])
b++;
else
w++;
if(p)
{
s1++;
e1.push_back(x);
}
else
{
s2++;
e2.push_back(x);
}
int i;
for(i=l.h[x];i;i=l.t[i])
dfs(l.v[i],p^1);
}
int build1()
{
for(auto v1:e)
{
int i;
for(i=l.h[v1];i;i=l.t[i])
{
int v2=l.v[i];
g1.add(v1,v2,1000,1);
g1.add(v2,v1,0,-1);
g1.add(v2,v1,1000,1);
g1.add(v1,v2,0,-1);
}
if(c[v1])
{
g1.add(g1.S,v1,1,0);
g1.add(v1,g1.S,0,0);
}
}
for(auto v1:e2)
{
g1.add(v1,g1.T,1,0);
g1.add(g1.T,v1,0,0);
}
return g1.maxflow();
}
int build2()
{
for(auto v1:e)
{
int i;
for(i=l.h[v1];i;i=l.t[i])
{
int v2=l.v[i];
g2.add(v1,v2,1000,1);
g2.add(v2,v1,0,-1);
g2.add(v2,v1,1000,1);
g2.add(v1,v2,0,-1);
}
if(c[v1])
{
g2.add(g2.S,v1,1,0);
g2.add(v1,g2.S,0,0);
}
}
for(auto v1:e1)
{
g2.add(v1,g2.T,1,0);
g2.add(g2.T,v1,0,0);
}
return g2.maxflow();
}
void rd(int &s)
{
int c;
while((c=getchar())<'0'||c>'9');
s=c-'0';
while((c=getchar())>='0'&&c<='9')
s=s*10+c-'0';
}
int main()
{
int n,m;
// scanf("%d%d",&n,&m);
rd(n);
rd(m);
int i;
scanf("%s",s+1);
for(i=1;i<=n;i++)
c[i]=s[i]-'0';
int x,y;
for(i=1;i<=m;i++)
{
// scanf("%d%d",&x,&y);
rd(x);
rd(y);
l.add(x,y);
l.add(y,x);
}
memset(vis,-1,sizeof vis);
ans=0;
g1.S=g2.S=n+1;
g1.T=g2.T=n+2;
for(i=1;i<=n;i++)
if(vis[i]==-1)
{
w=b=s1=s2=0;
e.clear();
e1.clear();
e2.clear();
dfs(i,0);
if(w!=s1&&w!=s2)
failed();
int ans1=0x7fffffff,ans2=0x7fffffff;
g1.clear();
g2.clear();
int f1,f2;
if(w==s1&&b==s2)
{
ans1=build1();
f1=g1.flow;
}
if(b==s1&&w==s2)
{
ans2=build2();
f2=g2.flow;
}
if(ans1<ans2)
{
ans+=ans1;
memcpy(g1.f,c,sizeof c);
while(f1--)
g1.getans();
}
else
{
ans+=ans2;
memcpy(g2.f,c,sizeof c);
while(f2--)
g2.getans();
}
}
printf("%d
",ans);
// for(auto v:a)
// printf("%d %d
",v.first,v.second);
for(i=1;i<=len;i++)
printf("%d %d
",ax[i],ay[i]);
return 0;
}