bzoj 1176 [Balkan2007]Mokia

Description

维护一个W*W的矩阵，初始值均为S.每次操作可以增加某格子的权值,或询问某子矩阵的总权值.修改操作数M<=160000,询问数Q<=10000,W<=2000000.

Input

第一行两个整数,S,W;其中S为矩阵初始值;W为矩阵大小

接下来每行为一下三种输入之一(不包含引号):

"1 x y a"

"2 x1 y1 x2 y2"

"3"

输入1:你需要把(x,y)(第x行第y列)的格子权值增加a

输入2:你需要求出以左下角为(x1,y1),右上角为(x2,y2)的矩阵内所有格子的权值和,并输出

输入3:表示输入结束

Output

对于每个输入2,输出一行,即输入2的答案

Sample Input

0 4
1 2 3 3
2 1 1 3 3
1 2 2 2
2 2 2 3 4
3

Sample Output

3
5

HINT

保证答案不会超过int范围

　　题目大意 （数据结构题题面太简洁不需要大意）

　　显然树套树加动态开点可以过掉这道题，然而表示并不想写。

　　由于支持离线可以考虑CDQ分治。

　　首先对于一个左上角在(1, 1)，右下角在(x, y)的矩阵的权值和，是可以求出来的。首先以x为第一关键字，y为第二关键字，opt为第三关键字排序，然后用树状数组维护y = i上的点权和。因为x坐标升序排序，所以这么做是正确的。

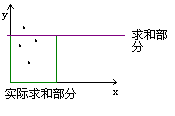
　　所以我们将一个询问拆成4个询问，再根据简单容斥计算出。

Code

  1 /**
  2  * bzoj
  3  * Problem#1176
  4  * Accepted
  5  * Time:6964ms
  6  * Memory:33940k
  7  */
  8 #include <bits/stdc++.h>
  9 using namespace std;
 10 typedef bool boolean;
 11 #ifndef WIN32
 12 #define Auto "%lld"
 13 #else
 14 #define Auto "%I64d"
 15 #endif
 16 
 17 #define lowbit(x) (x) & (-x)
 18 #define LL long long
 19 
 20 typedef class IndexedTree {
 21     public:
 22         int s;
 23         LL *lis;
 24         
 25         IndexedTree() {        }
 26         IndexedTree(int s):s(s) {
 27             lis = new LL[(s + 1)];
 28             memset(lis, 0, sizeof(LL) * (s + 1));
 29         }
 30         
 31         inline void add(int idx, int x) {
 32             for(; idx <= s; idx += lowbit(idx))
 33                 lis[idx] += x;
 34         }
 35         
 36         inline LL getSum(int idx) {
 37             LL ret = 0;
 38             for(; idx; idx -= lowbit(idx))
 39                 ret += lis[idx];
 40             return ret;
 41         }
 42 }IndexedTree;
 43 
 44 typedef class Query {
 45     public:
 46         int x;
 47         int y;
 48         int opt;
 49         int sign;
 50         int id;
 51         
 52         Query(int x = 0, int y = 0, int opt = 0, int sign = 0, int id = 0):x(x), y(y), opt(opt), sign(sign), id(id) {        }
 53         
 54         boolean operator < (Query b) const {
 55             if(x != b.x)    return x < b.x;
 56             if(y != b.y)    return y < b.y;
 57             return opt < b.opt;
 58         }
 59 }Query;
 60 
 61 int s, w;
 62 int cnt = 0;
 63 IndexedTree it;
 64 vector<Query> qs;
 65 vector<Query> bq;
 66 LL *res;
 67 
 68 inline void init() {
 69     int opt, x0, y0, x1, y1, c;
 70     scanf("%d%d", &s, &w);
 71     while(~scanf("%d", &opt) && opt != 3) {
 72         scanf("%d%d", &x0, &y0);
 73         if(opt == 1) {
 74             scanf("%d", &c);
 75             qs.push_back(Query(x0, y0, opt, c, cnt));
 76         } else {
 77             scanf("%d%d", &x1, &y1);
 78             qs.push_back(Query(x1, y1, opt, 1, cnt));
 79             qs.push_back(Query(x0 - 1, y1, opt, -1, cnt));
 80             qs.push_back(Query(x1, y0 - 1, opt, -1, cnt));
 81             qs.push_back(Query(x0 - 1, y0 - 1, opt, 1, cnt));
 82             bq.push_back(Query(x0, y0, x1, y1, cnt));
 83         }
 84         cnt++;
 85     }
 86 }
 87 
 88 void CDQDividing(int l, int r, vector<Query> &que) {
 89     if(que.empty())    return;
 90     if(l == r)    return;
 91     
 92     int mid = (l + r) >> 1;
 93     for(int i = 0; i < (signed)que.size(); i++) {
 94         if(que[i].opt == 1 && que[i].id <= mid)
 95             it.add(que[i].y, que[i].sign);
 96         if(que[i].opt == 2 && que[i].id > mid)
 97             res[que[i].id] += it.getSum(que[i].y) * que[i].sign;
 98     }
 99     
100     for(int i = 0; i < (signed)que.size(); i++)
101         if(que[i].opt == 1 && que[i].id <= mid)
102             it.add(que[i].y, -que[i].sign);
103     
104     vector<Query> ql, qr;
105     for(int i = 0; i < (signed)que.size(); i++)
106         if(que[i].id <= mid)
107             ql.push_back(que[i]);
108         else
109             qr.push_back(que[i]);
110     
111     que.clear();
112     CDQDividing(l, mid, ql);
113     CDQDividing(mid + 1, r, qr);
114 }
115 
116 inline void solve() {
117     res = new LL[(cnt + 1)];
118     memset(res, 0, sizeof(LL) * (cnt + 1));
119     sort(qs.begin(), qs.end());
120     it = IndexedTree(w);
121     CDQDividing(0, cnt - 1, qs);
122     
123     for(int i = 0; i < (signed)bq.size(); i++)
124         printf(Auto"
", res[bq[i].id] + (bq[i].opt - bq[i].x + 1) * (bq[i].sign - bq[i].y + 1) * s);
125 }
126 
127 int main() {
128     init();
129     solve();
130     return 0;
131 }