codeforces div2 C. Eugene and an array

题意：求非零连续子数组的个数
给定一个长度为 n 的数组 ar (n<=2e5)

问这个数组 ar 中有多少子数组是好数组

子数组的定义为：

　　把一个数组前面删去0个或全部元素，后面删去0个或全部元素得到的数组就是原数组的子数组

好数组的定义为：

　　对于数组 a 的每个子数组 b 都满足 sum{b} ≠ 0

　　则数组 a 就是个好数组

每个数组元素保证 abs(a[i])<=1e9
解法：思考一下可以发现如果一个数组不是好数组，例如：1 -1 那么在这个数组前后增加新的数字 1 1 -1 1 这个数组也不是一个好数组。
那么如何去计算符合题意的好数组的数量呢，最直接的想法就是去枚举（暴力）这样的复杂度是n^2,显然复杂度太大了，这时我们就可以用到前缀和来降低复杂度，
那么如何来判断一些连续子数组的和是否为0呢？
我们去查找当前的前缀和是否在前面得到过。

所以我们在处理某个元素ar[i]时，只看以ar[i]为右边界的子数组，r=i
从 i 位置开始往左寻找，直到将某个和为0的子数组包含进来后停止，令此时左边界为 l
那么 r-l 就是以ar[i]为右边界的好数组的个数（包含[r,r]、不包含[l,r]）
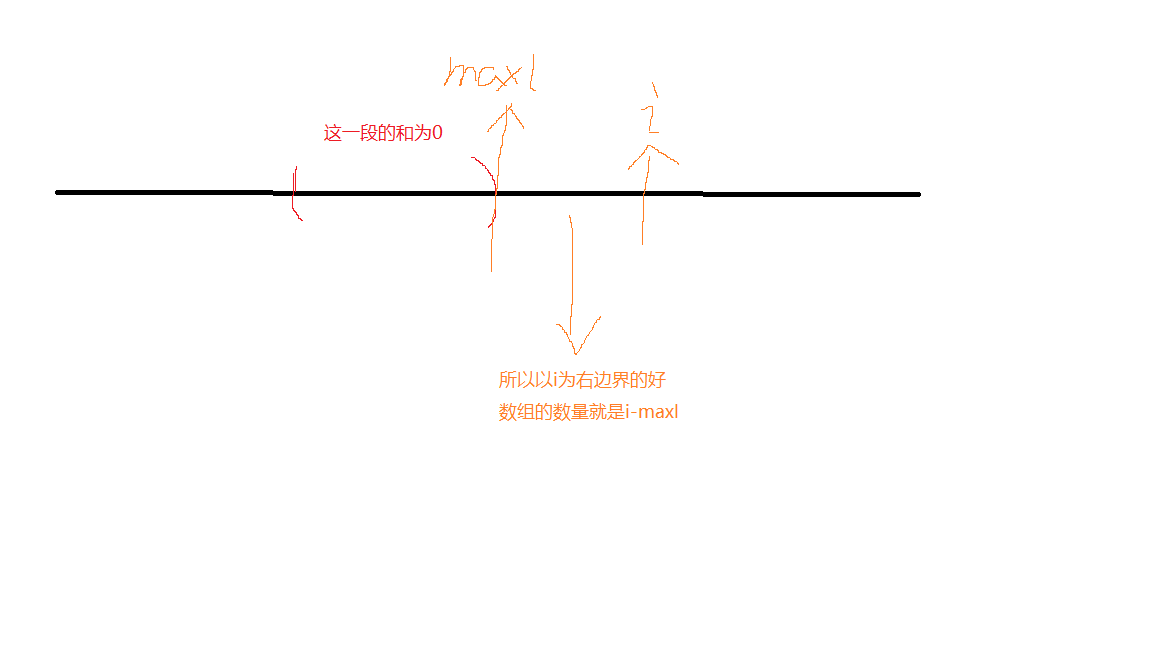
所以只要记录下 1 到 i 这段区间中，和为0的子数组的最大左边界maxL即可
每次答案加上 i-max

#pragma warning (disable:4996)
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define il inline
#define it register int
#define inf 0x3f3f3f3f
#define lowbit(x) (x)&(-x)
#define mem(a,b) memset(a,b,sizeof(a))
const int modd = 10000;
const int maxn = 65;
map<ll, ll>mp;
int main() {
	ll n,x,ans=0,maxl=1,sum=0;
	scanf("%lld", &n);
	mp[0] = 1;
	for (int i = 2; i <= n+1; i++) {
		scanf("%lld", &x);
		sum += x;
		if (mp[sum] != 0) maxl = max(maxl, mp[sum] + 1);
		ans += i - maxl;
		mp[sum] = i;
	}
	printf("%lld
", ans);
	system("pause");
	return 0;
}