85D Sum of Medians

传送门

题目

In one well-known algorithm of finding the k-th order statistics we should divide all elements into groups of five consecutive elements and find the median of each five. A median is called the middle element of a sorted array (it's the third largest element for a group of five). To increase the algorithm's performance speed on a modern video card, you should be able to find a sum of medians in each five of the array.

A sum of medians of a sorted k-element set S = {a₁, a₂, ..., a_k}, where a₁ < a₂ < a₃ < ... < a_k, will be understood by as

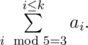
The 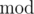operator stands for taking the remainder, that is 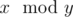stands for the remainder of dividing x by y.

To organize exercise testing quickly calculating the sum of medians for a changing set was needed.

Input

The first line contains number n (1 ≤ n ≤ 10⁵), the number of operations performed.

Then each of n lines contains the description of one of the three operations:

• add x — add the element x to the set;
• del x — delete the element x from the set;
• sum — find the sum of medians of the set.

For any add x operation it is true that the element x is not included in the set directly before the operation.

For any del x operation it is true that the element x is included in the set directly before the operation.

All the numbers in the input are positive integers, not exceeding 10⁹.

Output

For each operation sum print on the single line the sum of medians of the current set. If the set is empty, print 0.

Please, do not use the %lld specificator to read or write 64-bit integers in C++. It is preferred to use the cin, cout streams (also you may use the %I64d specificator).

题目大意

N个操作，add x：向集合中添加x；del x：删除集合中的x；sum：将集合排序后，将集合中所有下标i % 5 = 3的元素累加求和。

分析

首先，我们不难想出最基础思路，即在线段树上记录5个值，分别表示模5余i的位置的和。但是我们知道如果插入一个数x则他后面的数的位置必然集体加一，如果删除一个数则他后面的数的位置必然减一。所以我们在每一次插入或删除之后将此点之后区间的所有线段树节点的5个值交换一下即可。在有了大体思路之后我们再来考虑如何实现交换节点这一操作：我们将所有数离线读入并离散化，在每一次操作用rd数组记录此点是后移还是前移，所以某个节点的余数为i的值即为它的的左儿子余数为i的值+它的右儿子余数为（i-左儿子之后点在原有位置上集体移动的位数）的值。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cctype>
#include<cmath>
#include<cstdlib>
#include<queue>
#include<ctime>
#include<vector>
#include<set>
#include<map>
#include<stack>
using namespace std;
long long xx[110000],kd[110000],d[6][440000],rd[440000],b[110000];
map<long long,long long>id;
inline long long read(){
      long long x=0,f=1;char s=getchar();
      while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
      while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+(s-'0');s=getchar();}
      return f*x;
}
inline void update(long long le,long long ri,long long pl,long long k,long long wh,long long sum){
      if(le==ri){
          d[1][wh]+=k;
          rd[wh]+=sum;
          return;
      }
      long long mid=(le+ri)>>1;
      if(mid>=pl)update(le,mid,pl,k,wh<<1,sum);
        else update(mid+1,ri,pl,k,wh<<1|1,sum);
      rd[wh]=rd[wh<<1]+rd[wh<<1|1];
      for(long long i=0;i<5;i++)
         d[i][wh]=d[i][wh<<1]+d[(i-rd[wh<<1]%5+5)%5][wh<<1|1];
}
int main()
{     long long n,m,i,j,tot=0,sum=0;
      n=read();
      for(i=1;i<=n;i++){
         string s;
         cin>>s;
         if(s[0]=='a'){
            kd[i]=1;
            xx[i]=read();
            b[++tot]=xx[i];
         }else if(s[0]=='d'){
            kd[i]=2;
            xx[i]=read();
         }else kd[i]=3;
      }
      sort(b+1,b+tot+1);
      for(i=1;i<=tot;i++)
         if(!id[b[i]]){
           id[b[i]]=++sum;
         }
      for(i=1;i<=n;i++){
         if(kd[i]<3){
            update(1,n,id[xx[i]],(kd[i]==1?xx[i]:-xx[i]),1,(kd[i]==1?1:-1));
         }else printf("%lld
",d[3][1]);
      }
      return 0;
}