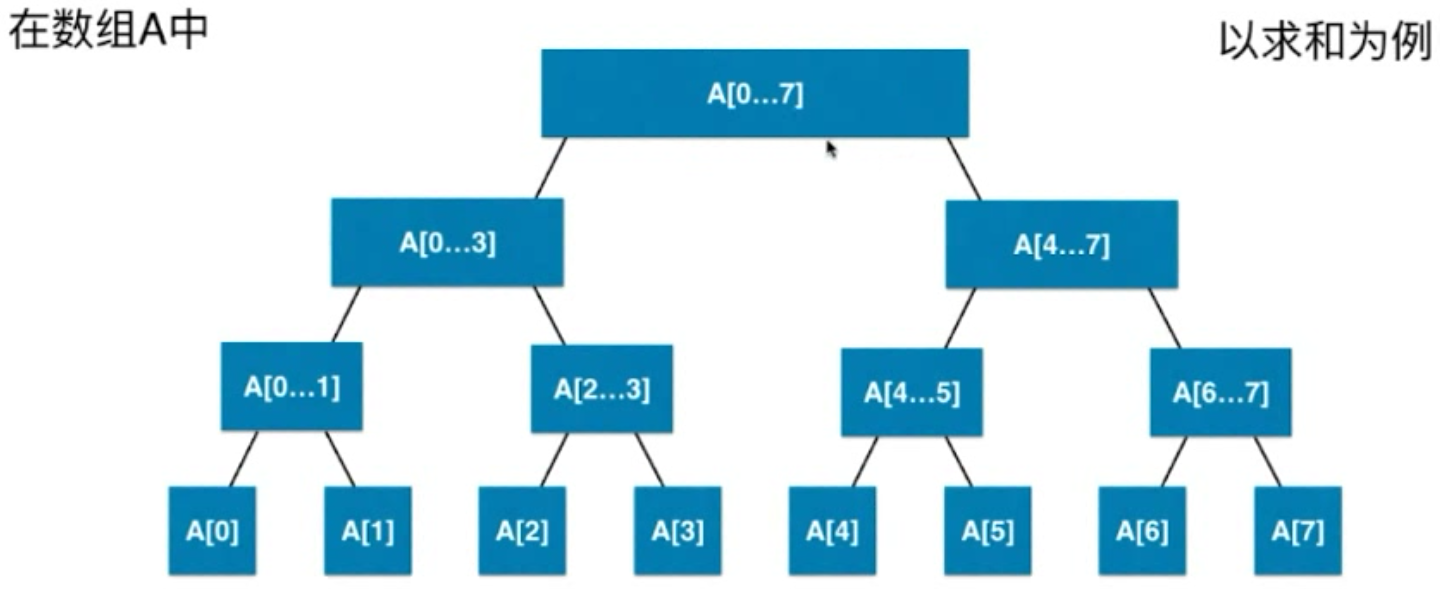
什么是线段树
概念
线段树是一种二元树形数据结构,1977年由Jon Louis Bentley发明,用以储存区间或线段,并且允许快速查询结构内包含某一点的所有区间。
一个包含 n 个区间的线段树,空间複杂度为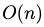 ,查询的时间複杂度则为,其中
,查询的时间複杂度则为,其中 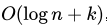 , 其中k是符合条件的区间数量。
, 其中k是符合条件的区间数量。
引例:
假设某大学有一面文化墙,各个学院都可以在上面涂色,要求涂色区域高必须和墙一样,宽度任意但必须是整数(以米为单位)。涂色可以覆盖其他学院的涂色。现在若干个学院涂色之后最终这面墙上能看见多少种颜色。

抽象出来就是m次操作后,我们可以在【i,j】 区间看见多少中颜色?
这个过程是两种操作:
1,染色(更新区间):改变区间的值
2,查询操作:查询指定区间的颜色数
当然可以用数组实现,时间复杂度 = O(n) + O(n) = O(n),显然不是很好的方案,
线段树在这里就很适合,这时时间复杂度都可以O(logn)
举例:
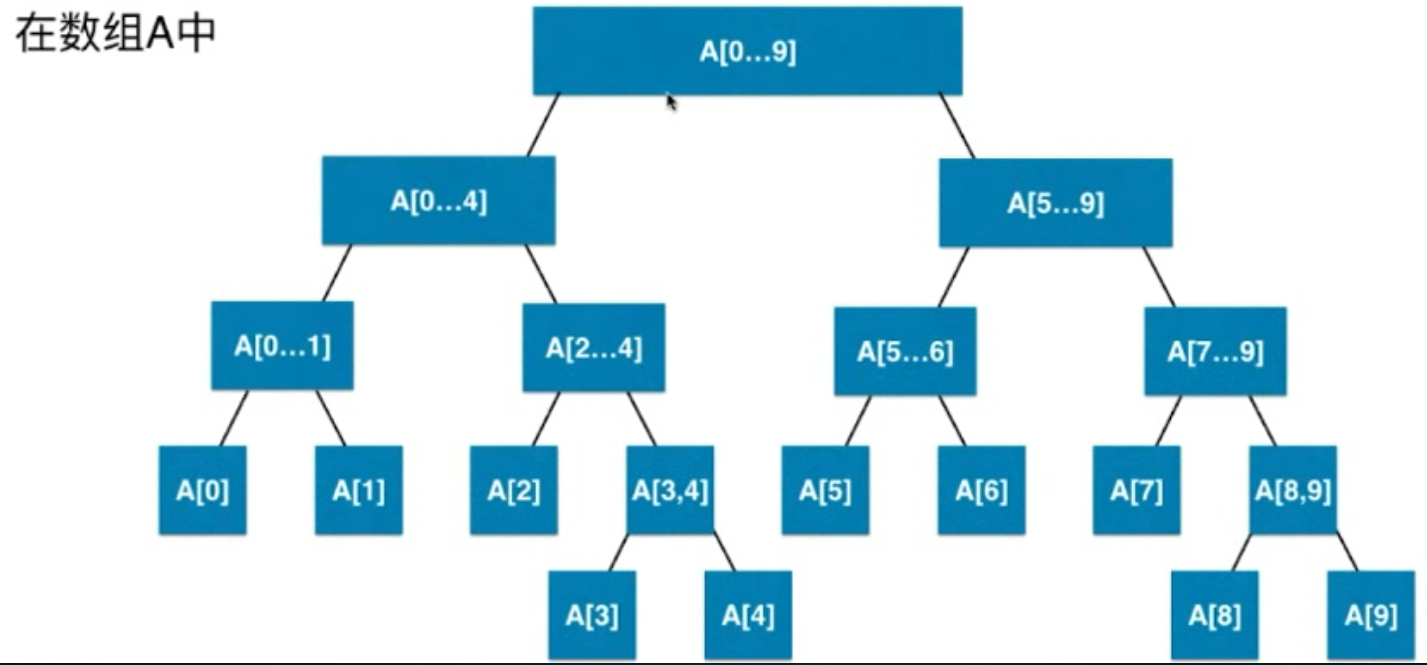
所以,线段树可能不是满的二叉树,也可能不是完全二叉树,但是,线段树是平衡二叉树,
平衡二叉树的简单定义:
是一种结构平衡的二叉搜索树,它是一种 每个节点的左右两子树高度差都不超过一 的二元树。它能在O( log n )内完成插入、查找和删除操作,最早被发明的平衡二叉搜索树为AVL树。
常见的平衡二叉搜索树有:
AVL树
红黑树
Treap(树堆 tree + heap )
节点大小平衡树
表示这颗树的数组大小问题:
因为线段树是平衡二叉树,所以我们可以用数组来表示它,
如何区间有n个元素,那么数组需要开辟多大呢?
如果n = 2^k ,数组需要 2*2^k - 1 (等比数列求和 2^0+...+2^k) , 所以要分配2n个。
如果最坏n = 2^k + 1 ,这时,多余的一个要放到下一层,数组需要4*2^k -1 (等比数列求和 2^0+...+2^k+2^(k+1) ), 此时造成的浪费最大, (不过无所谓,以空间换时间),所以要分配 4n个。
因此,答案就是4n,而且这里区间我们不考虑添加元素,即区间固定,数组只需要4n的静态空间即可,(注:很可能造成2n的浪费 问题,暂时不在乎)