农夫约翰在一所夜校学习算法课程,他刚刚学会了最小生成树。现在约翰意识到他的农场设计得不够高效,他想简化农场的布局。
约翰的农场可以看做一个图,农田代表图中顶点,田间小路代表图中的边,每条边有一定的长度。约翰注意到,农场中最多有三条小路有着相同的长度。约翰想删除一些小路使得农场成为一棵树,使得两块农田间只有一条路径。但是约翰想把农场设计成最小生成树,也就是农场道路的总长度最短。
请帮助约翰找出最小生成树的总长度,同时请计算出总共有多少种最小生成树?
按照 构造最小生成树,
由于题目中给出 的条件,
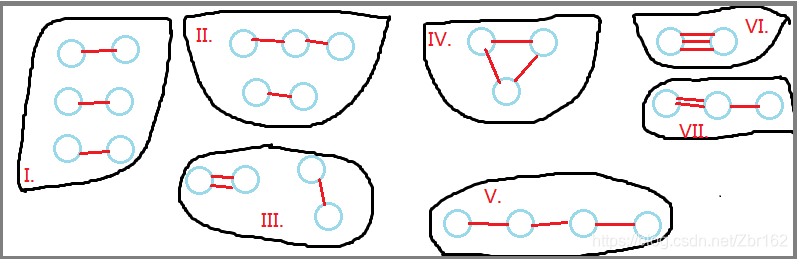
所以遇到 不同 的边有 相同 的边权时, 列举出所有加边时的情况进行分析
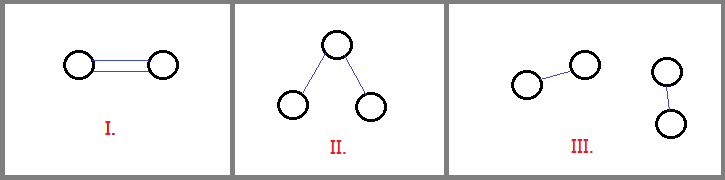
第一张图为 条边边权相同的情况, 第二张图为 条.
在 最小生成树算法加新的边时,
使用 辅助判断 碳碳双键,碳碳三键 等价的边 和 环,
用 维护参考了上方的题解.
#include<bits/stdc++.h>
#define reg register
const int maxn = 100005;
const int mod = 1e9 + 7;
int N;
int M;
int F[maxn];
int Find(int x){ return F[x]==x?x:F[x]=Find(F[x]); }
struct Edge{ int u, v, w; } E[maxn];
bool cmp(Edge a, Edge b){ return a.w < b.w; }
int main(){
freopen("a.in", "r", stdin);
freopen("a.out", "w", stdout);
scanf("%d%d", &N, &M);
for(reg int i = 1; i <= M; i ++) scanf("%d%d%d", &E[i].u, &E[i].v, &E[i].w);
for(reg int i = 1; i <= N; i ++) F[i] = i;
std::sort(E+1, E+M+1, cmp);
int Ans_1 = 0, Ans_2 = 1;
for(reg int i = 1; i <= M; i ++){
typedef std::pair <int, int> pr;
std::set <pr> S;
int t, x = 0, y = 0;
for(t = i; t <= M; t ++){
if(E[t].w != E[i].w) break ;
int a = E[t].u, b = E[t].v;
S.insert(pr(std::min(a, b), std::max(a, b)));
}
x = t - i; t --;
for(; i <= t; i ++){
int a = Find(E[i].u), b = Find(E[i].v);
if(a != b) F[b] = a, y ++, Ans_1 = (1ll*Ans_1 + E[i].w) % mod;
}
i --;
if(x == 2 && y == 1) Ans_2 = 2ll*Ans_2 % mod;
else if(x == 3){
if(y == 1) Ans_2 = 3ll*Ans_2 % mod;
else if(y == 2) Ans_2 = 2ll*Ans_2 % mod;
}
}
printf("%d %d
", Ans_1, Ans_2);
return 0;
}