Sorting Slides
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 4812 | Accepted: 1882 |
Description
Professor Clumsey is going to give an important talk this afternoon. Unfortunately, he is not a very tidy person and has put all his transparencies on one big heap. Before giving the talk, he has to sort the slides. Being a kind of minimalist, he wants to do this with the minimum amount of work possible.
The situation is like this. The slides all have numbers written on them according to their order in the talk. Since the slides lie on each other and are transparent, one cannot see on which slide each number is written.
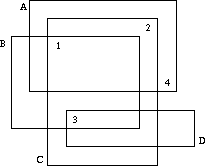
Well, one cannot see on which slide a number is written, but one may deduce which numbers are written on which slides. If we label the slides which characters A, B, C, ... as in the figure above, it is obvious that D has number 3, B has number 1, C number 2 and A number 4.
Your task, should you choose to accept it, is to write a program that automates this process.
The situation is like this. The slides all have numbers written on them according to their order in the talk. Since the slides lie on each other and are transparent, one cannot see on which slide each number is written.

Well, one cannot see on which slide a number is written, but one may deduce which numbers are written on which slides. If we label the slides which characters A, B, C, ... as in the figure above, it is obvious that D has number 3, B has number 1, C number 2 and A number 4.
Your task, should you choose to accept it, is to write a program that automates this process.
Input
The input consists of several heap descriptions. Each heap descriptions starts with a line containing a single integer n, the number of slides in the heap. The following n lines contain four integers xmin, xmax, ymin and ymax, each, the bounding coordinates of the slides. The slides will be labeled as A, B, C, ... in the order of the input.
This is followed by n lines containing two integers each, the x- and y-coordinates of the n numbers printed on the slides. The first coordinate pair will be for number 1, the next pair for 2, etc. No number will lie on a slide boundary.
The input is terminated by a heap description starting with n = 0, which should not be processed.
This is followed by n lines containing two integers each, the x- and y-coordinates of the n numbers printed on the slides. The first coordinate pair will be for number 1, the next pair for 2, etc. No number will lie on a slide boundary.
The input is terminated by a heap description starting with n = 0, which should not be processed.
Output
For each heap description in the input first output its number. Then print a series of all the slides whose numbers can be uniquely determined from the input. Order the pairs by their letter identifier.
If no matchings can be determined from the input, just print the word none on a line by itself.
Output a blank line after each test case.
If no matchings can be determined from the input, just print the word none on a line by itself.
Output a blank line after each test case.
Sample Input
4 6 22 10 20 4 18 6 16 8 20 2 18 10 24 4 8 9 15 19 17 11 7 21 11 2 0 2 0 2 0 2 0 2 1 1 1 1 0
Sample Output
Heap 1 (A,4) (B,1) (C,2) (D,3) Heap 2 none
Source
题目大意:给出n个矩形的坐标和n个点的坐标,每个矩形上最多只能有一个点,问是否有点一定属于某个矩形.
分析:矩形与点配对,非常像是二分图匹配.最后要求的实际上是二分图的最大匹配中必须留下的边.因为最大匹配找的边是删掉以后很容易使得匹配数变小的边,所以枚举最大匹配中的边,删掉后看看最大匹配数是否减小,如果是,那么这条边就是必须的.
犯了一个错:两个dfs函数弄混了,导致在第二个dfs函数中调用了第一个函数QAQ,以后这种函数还是根据功能来命名的好.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; int n,a[55][55],pipei[55],flag[55],can[55][55],cnt,ans[55][55],cas; int pipei2[55]; bool print = false; struct node { int minx,maxx,miny,maxy; } e[55]; struct node2 { int x,y; } point[55]; bool dfs(int u) { for (int i = 1; i <= n; i++) if (a[u][i] && !flag[i]) { flag[i] = 1; if (!pipei[i] || dfs(pipei[i])) { pipei[i] = u; return true; } } return false; } bool dfs2(int u) { for (int i = 1; i <= n; i++) if (a[u][i] && !flag[i]) { flag[i] = 1; if (!pipei2[i] || dfs2(pipei2[i])) { pipei2[i] = u; return true; } } return false; } int main() { while (scanf("%d",&n) && n) { memset(pipei,0,sizeof(pipei)); memset(can,0,sizeof(can)); memset(ans,0,sizeof(ans)); memset(a,0,sizeof(a)); cnt = 0; print = false; for (int i = 1; i <= n; i++) scanf("%d%d%d%d",&e[i].minx,&e[i].maxx,&e[i].miny,&e[i].maxy); for (int i = 1; i <= n; i++) scanf("%d%d",&point[i].x,&point[i].y); for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) if (point[j].x >= e[i].minx && point[j].x <= e[i].maxx && point[j].y >= e[i].miny && point[j].y <= e[i].maxy) a[j][i] = 1; for (int i = 1; i <= n; i++) { memset(flag,0,sizeof(flag)); if (dfs(i)) cnt++; } for (int i = 1; i <= n; i++) { a[pipei[i]][i] = 0; int cnt2 = 0; memset(pipei2,0,sizeof(pipei2)); for (int j = 1; j <= n; j++) { memset(flag,0,sizeof(flag)); if(dfs2(j)) cnt2++; } if (cnt2 < cnt) ans[i][pipei[i]] = 1; a[pipei[i]][i] = 1; } printf("Heap %d ",++cas); for (int i = 1; i <= n; i++) if (ans[i][pipei[i]]) { print = true; printf("(%c,%d) ",'A' + i - 1,pipei[i]); } if (!print) printf("none"); printf(" "); } return 0; }