汉诺塔模型推广 -> n盘4塔问题

经典汉诺塔问题理解方法：

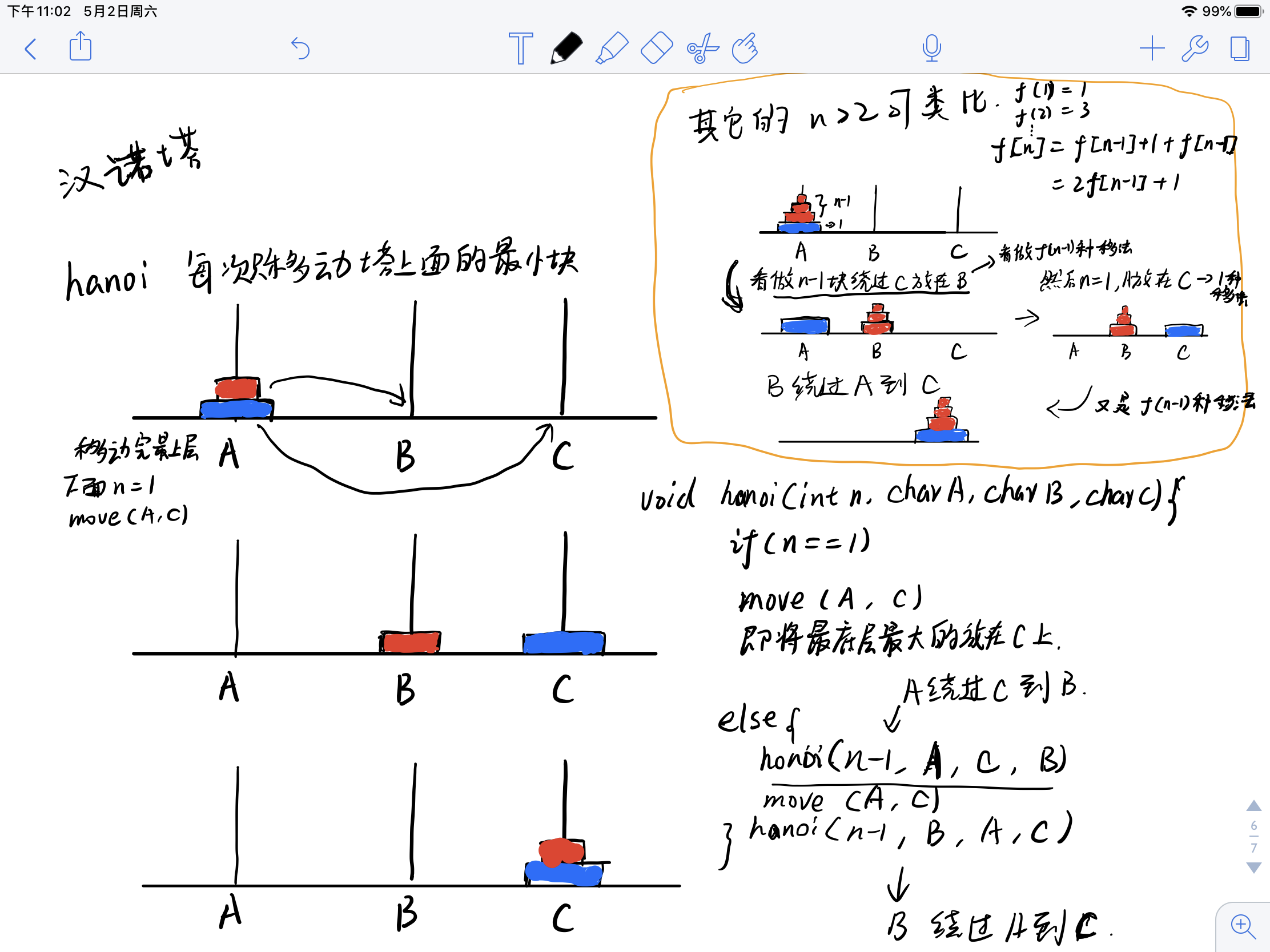
 经典汉诺塔问题代码（当三个塔时，答案为 2ⁿ - 1）

d[n]表示求解该n盘3塔问题的最小步数 显然有d[n]=2*d[n-1]+1

即把前n-1个盘子从A柱（绕过C柱）移动到B柱，然后把第n个盘子从A柱移动到C柱，最后把前n-1个盘子从B柱（绕过A柱）移动到C柱

#include <iostream>

using namespace std;

void hanoi(int n, char A, char B, char C) {
    if (n == 1) {
        cout << A << "->" << C << endl;
    }
    else {
        hanoi(n - 1, A, C, B);
        cout << A << "->" << C << endl;
        hanoi(n - 1, B, A, C);
    }
}

int main() {
    hanoi(2, 'A', 'B', 'C');
    return 0;
}

 汉诺塔四塔问题：

链接：https://www.acwing.com/problem/content/98/

【题意】

本题大意是求n个盘子四座塔的hanoi问题的最少步数。输出n为1～12个盘子时各自的答案。

【分析】

汉罗塔改编的一个小问题。

首先考虑n个盘子3座塔的经典hanoi问题，设d[n]表示求解该n盘3塔问题的最少步数：

①把前n-1个盘子从A柱移动到B柱（需要d[n-1]步）

②把第n个盘子从A柱移动到C柱   （需要1步）

③把前n-1个盘子从B柱移动到C柱（需要d[n-1]步）

显然总计d[n]=2*d[n-1]+1 此过程属于dp+递归问题

----------------------------------------------------------------------------------------

那么对于此问题，设f[n]表示求解n盘4塔问题的最小步数：

①把i个盘子在4塔模式下移动到B柱（需要f[i]步）

②把n-i个盘子在3塔模式下移动到D柱   （需要d[n-i]步）

③把i个盘子在4塔模式下移动到D柱（需要f[i]步）

考虑所有可能的i取最小值得：f[n]=min{ 2 * f[i] + d[n-i] }，i属于[1, i)

#include <iostream>
#include <cstring>

using namespace std;

int main()
{
    int d[15], f[15]; // d表示n盘3塔的方案数 f表示n盘4塔的方案数
    
    d[1] = 1;
    for (int i = 2; i <= 12; i ++ ) {
        d[i] = 1 + d[i - 1] * 2;
    }
    
    memset(f, 0x3f, sizeof f);
    f[0] = 0;
    for (int i = 1; i <= 12; i ++ )
        for (int j = 0; j < i; j ++ )
            f[i] = min(f[i], f[j] * 2 + d[i - j]);
    
    for (int i = 1; i <= 12; i ++ ) cout << f[i] << endl;
    
    return 0;
}