【洛谷5月月赛】回首过去（数论分块）

chedan

如果你会数论分块的话这题就是一眼题，可惜我考比赛时还并不会/kk。

搞了半天通过一些思索+打表找规律自己yy出来数论分块这个东西。

题目链接

---

题意

Solution

$frac{x}{y}$能写成十进制有限小数当且仅当它化成最简形式时分母分解质因数只有2和5两个质因子。

我们可以枚举其最简分数下的分母为$2^a5^b$。

之后再枚举其前面的系数设为k，这个系数的约数不能有2或5，要不然可能会算重。现在要找有多少k的倍数。预处理前缀和，只需找$sum[n/(2^a5^b)]$即可。

考虑如何快速预处理。

先不考虑2,5倍数的问题，所求即为$sum_{i=1}^n [frac{n}{i}]$。

我们需要在至多$sqrt{N}$的时间内预处理。

这就用到了我们的数论分块。

我们不妨枚举一下每个i的$[frac{n}{i}]$。

比如当$n=16$时。

我们发现后面有大量重复的。实际上只有$2sqrt{N}-1$个不同的值。

这是巧合吗？再看$n=24$的情况。

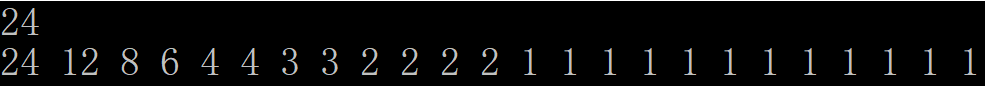
这回只有8个不同的。我们想这些不同的有没有什么联系？

我们发现：

24/1=24

24/2=12

24/3=8

24/4=6

而正好$(12,24]$的值都是1，$(8,12]$的值都是2，$(6,8]$的值都为3，而$(4,6]$的值都为4。

所以我们其实只用存$2sqrt{N}$左右个数就可以表示出所有可能的值。这很好理解。

然后将这些值预处理出来再用个容斥把2,5弄掉。查询时二分查找即可。

总时间复杂度$O(sqrt{N}+log^2{N})$

代码有点小丑。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
ll n, now = 1, nnow;
ll ans, cnt;
ll zcr[10000010], top;
ll zsy[10000010];
ll f(ll x, ll a) {
    return x / a;
}
ll cal(ll l, ll r) {
    return f(r, 2) - f(l - 1, 2) + f(r, 5) - f(l - 1, 5) - f(r, 10) + f(l - 1, 10);
}
ll find(ll x) {
    ll l = 1, r = top, ret = -1;
    while (l <= r) {
        ll mid = (l + r) >> 1;
        if (zcr[mid] > x) {
            ret = mid;
            r = mid - 1;
        } else {
            l = mid + 1;
        }
    }
    return ret;
}
ll sum(ll x) {
    ll f = find(x);
    ll ret = zsy[f - 2];
    ll val = n / zcr[f - 1];
    ret += val * (x - zcr[f - 1] + 1);
    ret -= val * cal(zcr[f - 1], x);
    return ret;
}
int main() {
    cin >> n;
    for (ll i = 1; i * i <= n; i++) {
        zcr[++top] = i;
        if (i * i < n) zcr[++top] = n / (i + 1) + 1;
    }
    zcr[++top] = n + 1;
    sort(zcr + 1, zcr + top + 1);
    for (int i = 1; i < top; i++) {
        ll val = n / zcr[i];
        zsy[i] = val * (zcr[i + 1] - zcr[i]);
        zsy[i] -= val * cal(zcr[i], zcr[i + 1] - 1);
        zsy[i] += zsy[i - 1];
    }
    while (now <= n) {
        nnow = now;
        while (nnow <= n) {
            nnow *= 5;
        }
        now *= 2;
    }
    now = 1;
    while (now <= n) {
        nnow = now;
        while (nnow <= n) {
            ll haha = sum(n / nnow);
            ans += haha;
            nnow *= 5;
        }
        now *= 2;
    }
    cout << ans;
    return 0;
}

update：

自己yy果真不太行，其实有一种更简单的求出分块的点的方法。

假设当前块的起点为$i$，则其终点$j=n/(n/i)$。每次令$i=j+1$即可。

这种写法预处理的代码：

for (ll i = 1, j; i <= n; i = j + 1) {
    zcr[++top] = i;
    j = n / (n / i);
    ll val = n / i;
    zsy[top] = val * (j - i + 1);
    zsy[top] -= val * cal(i, j);
    zsy[top] += zsy[top - 1];
}
zcr[++top] = n + 1;