机器学习算法详解（三）——通过损失函数优化看线性回归

我们知道机器学习中模型的参数是通过不断减小损失函数loss来进行优化的，这就与线性回归的含义不谋而合，只不过线性回归是通过最小二乘法来最小化误差（的平方）并且寻找最优函数。一想到平方，又不难联系到平方损失函数，平方损失函数相比最小二乘法不过就是多了个 1/n ，即求平均的系数。

假设模型预测值为y_i，模型实际输出为 a_i，则有：

平方损失函数公式：loss = (1/N)Σ(y_i - a_i)²

最小二乘法公式：e = Σ(y_i - a_i)² （由于回归方程的随机误差期望为0且无法确定，此处忽略）

可以看出两者并没有本质区别，都可以理解成通过最小化误差的平方和来优化模型参数。

下面使用tensorflow模拟一下损失函数的优化过程，完整代码如下：

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

batch_size = 10
seed = 23445

# 通过随机数种子生成模型的输入输出
random = np.random.RandomState(seed)
input_x = random.rand(64,2)
input_y = [[x1+x2+random.rand()/10.0-0.05] for (x1,x2) in input_x]
print(input_x)
print(input_y)
x = input_x[:,0]
y = input_x[:,1]
z = input_y
# 绘制3D散点图，查看分布情况
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(x, y, z)

ax.set_zlabel('Z', fontdict={'size': 15, 'color': 'red'})
ax.set_ylabel('Y', fontdict={'size': 15, 'color': 'red'})
ax.set_xlabel('X', fontdict={'size': 15, 'color': 'red'})
plt.show()

# 定义网络输入和输出以及参数
x = tf.placeholder(tf.float32,shape=(None,2))
y_ = tf.placeholder(tf.float32,shape=(None,1))
w = tf.Variable(tf.random_normal([2,1],stddev=1,seed=1))
y = tf.matmul(x,w)

# 定义损失函数为MSE
loss = tf.reduce_mean(tf.square(y-y_))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)

# 生成会话，训练10000轮
with tf.Session() as sess:
    init = tf.global_variables_initializer()
    sess.run(init)
    steps = 10000
    for i in range(steps):
        start = (i*batch_size)%64
        end = (i*batch_size)%64+batch_size
        sess.run(train_step,feed_dict={x:input_x[start:end],y_:input_y[start:end]})
        if i%500 ==0:
            print("after ",i," steps,w is :",sess.run(w),"loss is :",sess.run(loss,feed_dict={x:input_x[start:end],y_:input_y[start:end]}),'
')
    print("final,w is :",sess.run(w),"loss is :",sess.run(loss,feed_dict={x:input_x[start:end],y_:input_y[start:end]}),'
')

生成数据如下：

  

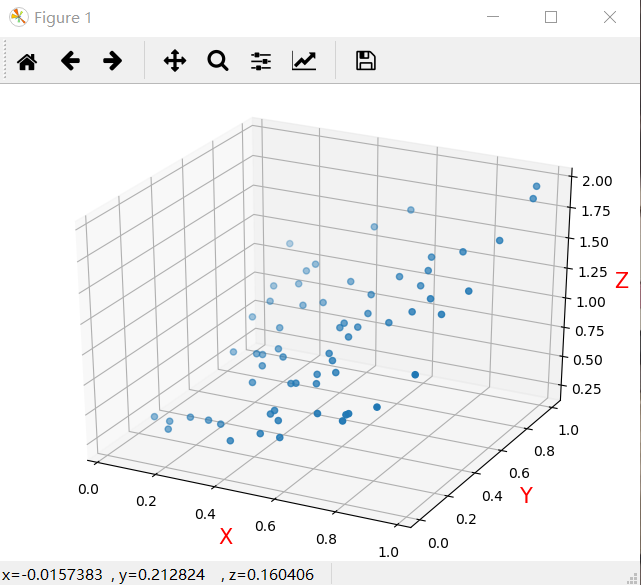
首先可以看到散点分布如图

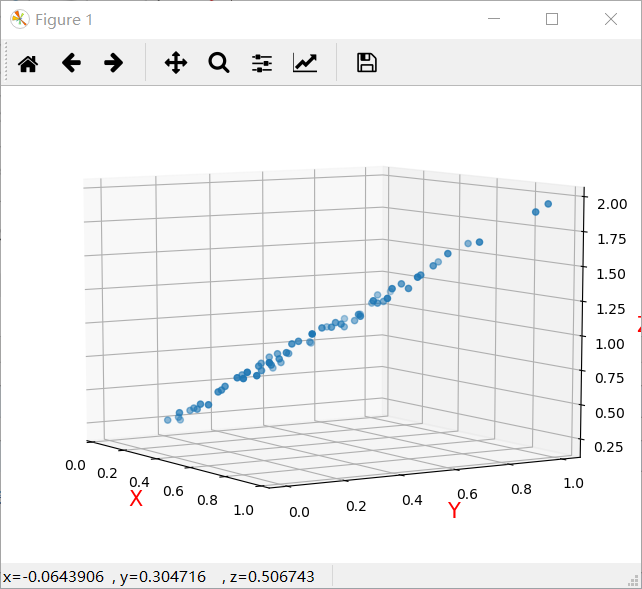
旋转一下方向可以看到，生成的数据是存在一定线性关系的

参数调优过程如下：

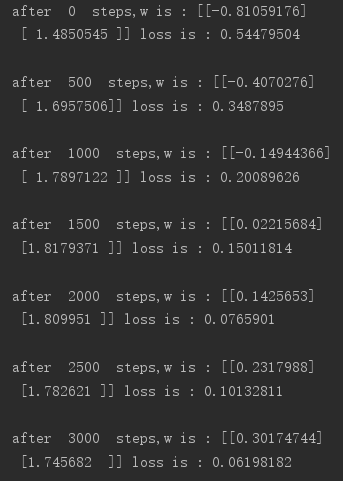
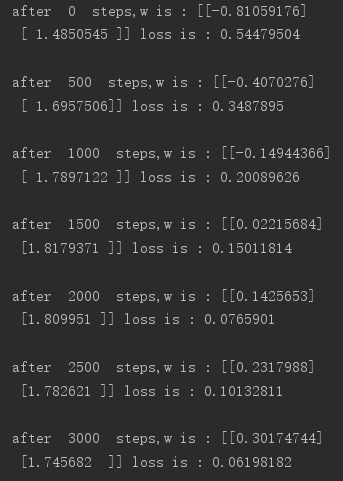
可以看到loss大致是在不断减小的，最终结果如下：

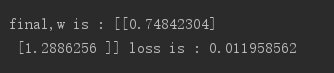
由上述过程可以看出，损失函数和线性回归存在一定的相似性，但是需要注意的是线性回归只能处理线性问题，而损失函数可以处理非线性的复杂模型。

感兴趣的读者可以修改上述代码实现线性回归原理。