问题:
Kruskal算法构造最小生成树的过程。
解析:
Kruskal算法的基本思路:
对于所有的边,每次取一条最短的边(不能重复取),判断它的两个端点是否已经在一个连通块中了(并查集维护),如果是,那么取下一条边;如果没在一个连通块中,则把两个连通块(不一定是两个点)连在一起,答案加上当前边的长度。直到所有的点都在一个连通块中结束。
解析图:
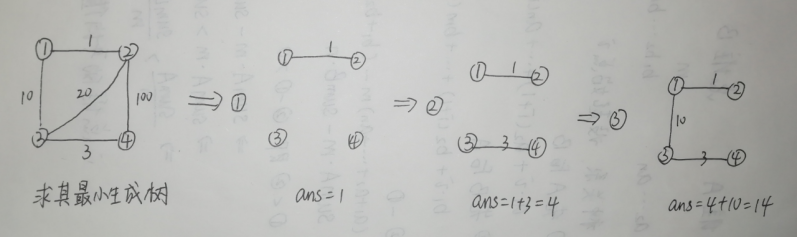
设计(核心代码):
1 int kruskal()
2 {
3 for(int i=1;i<=tot;++i) q.push(p[i]);//把所有的边放入优先队列
4 while(cnt!=n-1)
5 {
6 edge x=q.top();
7 q.pop();
8 while(find(x.u)==find(x.v)) x=q.top(),q.pop();
9 ba(x.u,x.v);
10 cnt++;
11 ans+=x.w;
12 }
13 return ans;
14 }
源码:
https://github.com/Big-Kelly/Algorithm

1 #include<bits/stdc++.h>
2 #include <set>
3 #include <map>
4 #include <stack>
5 #include <cmath>
6 #include <queue>
7 #include <cstdio>
8 #include <string>
9 #include <vector>
10 #include <cstring>
11 #include <iostream>
12 #include <algorithm>
13
14 #define ll long long
15 #define PLL pair<ll,ll>
16 #define PII pair<int,int>
17 #define bug printf("*********
")
18 #define FIN freopen("input.txt","r",stdin);
19 #define FON freopen("output.txt","w+",stdout);
20 #define IO ios::sync_with_stdio(false),cin.tie(0)
21 #define ls root<<1
22 #define rs root<<1|1
23
24 using namespace std;
25 const int inf=0x3f3f3f3f;
26 const ll Inf=1e18+7;
27 const int maxn=1e4+5;
28 const int mod=1e9+7;
29
30 struct Kruskal
31 {
32 //结构体存边
33 struct edge
34 {
35 int u,v,w;
36 }p[maxn];
37
38 int tot;
39
40 void add(int u,int v,int w)
41 {
42 p[++tot].v=v;
43 p[tot].w=w;
44 p[tot].u=u;
45 }
46
47 int fa[maxn],n;//并查集。
48
49 void init()//初始化
50 {
51 tot=0;
52 for(int i=1;i<=n;++i) fa[i]=i;
53 }
54
55 //优先队列处理最短边
56 struct cmp
57 {
58 bool operator()(const edge &a,const edge &b)
59 {
60 return a.w>b.w;
61 }
62 };
63 priority_queue<edge,vector<edge>,cmp > q;
64
65 //并查集
66 int find(int x)
67 {
68 return fa[x]==x?x:fa[x]=find(fa[x]);
69 }
70
71 void ba(int x,int y)
72 {
73 int px=find(x),py=find(y);
74 fa[px]=py;
75 }
76
77 int ans=0,cnt=0;
78
79 int kruskal()
80 {
81 for(int i=1;i<=tot;++i) q.push(p[i]);//把所有的边放入优先队列
82 while(cnt!=n-1)
83 {
84 edge x=q.top();
85 q.pop();
86 while(find(x.u)==find(x.v)) x=q.top(),q.pop();
87 ba(x.u,x.v);
88 cnt++;
89 ans+=x.w;
90 }
91 return ans;
92 }
93 };
94
95 int n,m;
96
97 int main()
98 {
99 freopen("in.txt","r",stdin);
100 freopen("out.txt","w",stdout);
101 Kruskal k;
102 scanf("%d %d",&n,&m);
103 k.n=n;
104 k.init();
105 while(m--)
106 {
107 int u,v,w;
108 scanf("%d %d %d",&u,&v,&w);
109 k.add(u,v,w);
110 }
111 printf("%d
",k.kruskal());
112 }
