codeforces 690C3 C3. Brain Network (hard)(lca)

题目链接：

C3. Brain Network (hard)

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Breaking news from zombie neurology! It turns out that – contrary to previous beliefs – every zombie is born with a single brain, and only later it evolves into a complicated brain structure. In fact, whenever a zombie consumes a brain, a new brain appears in its nervous system and gets immediately connected to one of the already existing brains using a single brain connector. Researchers are now interested in monitoring the brain latency of a zombie. Your task is to write a program which, given a history of evolution of a zombie's nervous system, computes its brain latency at every stage.

Input

The first line of the input contains one number n – the number of brains in the final nervous system (2 ≤ n ≤ 200000). In the second line a history of zombie's nervous system evolution is given. For convenience, we number all the brains by 1, 2, ..., n in the same order as they appear in the nervous system (the zombie is born with a single brain, number 1, and subsequently brains 2, 3, ..., n are added). The second line contains n - 1 space-separated numbers p2, p3, ..., pn, meaning that after a new brain k is added to the system, it gets connected to a parent-brain .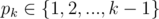

Output

Output n - 1 space-separated numbers – the brain latencies after the brain number k is added, for k = 2, 3, ..., n.

Example

input

6
1
2
2
1
5

output

1 2 2 3 4 

题意：

给一棵树的生成过程,问在每次添加一个节点后这棵树的直径是多少;

思路：

在新加的一个节点w前的直径是(u,v),加入w后,直径就变成了max{(u,v)(u,w)(v,w)};
然后就是把lca约束成RMQ问题来了;

AC代码：

#include <bits/stdc++.h>
/*
#include <vector>
#include <iostream>
#include <queue>
#include <cmath>
#include <map>
#include <cstring>
#include <algorithm>
#include <cstdio>
*/
using namespace std;
#define For(i,j,n) for(int i=j;i<=n;i++)
#define mst(ss,b) memset(ss,b,sizeof(ss));
typedef  long long LL;
template<class T> void read(T&num) {
    char CH; bool F=false;
    for(CH=getchar();CH<'0'||CH>'9';F= CH=='-',CH=getchar());
    for(num=0;CH>='0'&&CH<='9';num=num*10+CH-'0',CH=getchar());
    F && (num=-num);
}
int stk[70], tp;
template<class T> inline void print(T p) {
    if(!p) { puts("0"); return; }
    while(p) stk[++ tp] = p%10, p/=10;
    while(tp) putchar(stk[tp--] + '0');
    putchar('
');
}

const LL mod=1e9+7;
const double PI=acos(-1.0);
const LL inf=1e18;
const int N=2e5+10;
const int maxn=1005;
const double eps=1e-10;


int n,in[N],a[2*N],dep[N],cnt=0,dp[2*N][21],dis[N];
vector<int>ve[N];

void dfs(int x,int deep)
{
    //cout<<x<<" "<<deep<<endl;
    in[x]=cnt;
    a[cnt++]=x;
    dep[x]=deep;
    int len=ve[x].size();
    For(i,0,len-1)
    {
        int y=ve[x][i];
        dis[y]=dis[x]+1;
        dfs(y,deep+1);
        a[cnt++]=x;
    }
}

int RMQ()
{
    for(int i=0;i<cnt;i++)
        dp[i][0]=a[i];

    for(int j=1;(1<<j)<=cnt;j++)
    {
        for(int i=0;i+(1<<j)-1<cnt;i++)
        {
            if(dep[dp[i][j-1]]<dep[dp[i+(1<<(j-1))][j-1]])dp[i][j]=dp[i][j-1];
            else dp[i][j]=dp[i+(1<<(j-1))][j-1];
        }
    }
}
int query(int l ,int r)
{
    if(l>r)swap(l,r);
    int temp=(int)(log((r-l+1)*1.0)/log(2.0));
    if(dep[dp[l][temp]]<dep[dp[r-(1<<temp)+1][temp]])return dp[l][temp];
    return dp[r-(1<<temp)+1][temp];
}
int s=1,e=1,pre=0;
int check(int x,int y)
{
    //cout<<x<<" "<<y<<" "<<pre<<" @@@@"<<endl;
    int temp=query(in[x],in[y]);
    if(dis[x]+dis[y]-2*dis[temp]>pre)
    {
        s=x;
        e=y;
        pre=dis[x]+dis[y]-2*dis[temp];
    }
}

int main()
{
        read(n);
        int u;
        For(i,2,n)
        {
            read(u);
            ve[u].push_back(i);
        }
        dis[1]=0;
        dfs(1,0);
        RMQ();
        For(i,2,n)
        {
            int fs=s,fe=e;
            check(fs,fe);
            check(fs,i);
            check(fe,i);
            cout<<pre<<" ";
        }

        return 0;
}