本系列同步发布于本人的知乎专栏:确定性随机
最新想开始再系统学习一次数理统计和随机过程方便的知识,但是耽搁了一段时间,主要原因是不知道从哪里开始。最近,刚好在网上“随机”地买了一本《随机模拟方法与应用》(肖柳青&周石鹏 编著),于是就决定从这本书开始吧。
给自己一个目标:看看自己能不能完整地些一个系列的读书笔记。
1. 随机模拟可以解决什么样的问题
在现实生活中,我们面对的很对问题都带有随机性,解决这类问题要使用能处理随机性特征的数学工具——概率与数理统计。用概率论来描述随机系统的特征有一个很大的缺陷:很多用于描述系统特征的概率模型的求解十分困难,除极少数情况外很难获得到数学上的解析解。
随机模拟则通过对系统进行仿真,获取系统的状态变化和输出结果的数据。通过大量随机试验,获取并分析数据,在可接受的误差范围内估算系统行为的关键特征量。计算机是目前进行随机模拟的重要工具。
随机模拟对数学的要求相对较低,且模拟的过程简单且直观,能够让人很直观地了解系统行为的过程与结果。很多的数学模型是无法通过数学来直接求出它的解,它们只是描述了客观世界的逻辑关系(但这样也称为数学模型)。
2. 随机模拟的步骤
一个随机模拟的步骤一般分为以下几步:
(1) 确定描述系统状态的变量。清楚说明被模拟的系统情况,包括:输入、状态和输出,发生随机的条件是什么?这里的系统有必要对现实情况进行一定的简化;
(2) 设置变量。为系统的输入、状态和输出系统设置变量,被设置某种类型的随机数对应于随机事件;
(3) 运行规则。写出系统运行的基本逻辑,系统状态是如何变化的,即状态是如何更新的,那种类型的随机数是如何产生的;
(4)模拟系统。给定系统的初始状态,通过模拟系统的运行,给出系统的输出;
(5)抽样与统计。大量重复上述的随机实验,对结果进行统计,求出样本的均值。至于进行多少次的模拟,基本要求是:大量地地重复实验,直到要求出的结果稳定为止。
(6)对结果进行解析。对得到的结果进行模拟,必要的时候对前面的模拟过程进行修改并重新再进行一次,对结果进行比较。
随机模拟关注的是对实际问题的解决,并非将关注点聚焦于数学问题的求解上。因此,随机模拟的关键点是对实际问题的系统化建模描述,确定那些过程是通过随机来实现。
3. 蒙提霍尔问题(Monty Hall Problem)
书中举了好几个用随机模拟解决实际问题的例子,我这里摘录几个有意思的,第一个就是所谓的蒙提霍尔问题(Monty Hall Problem)。所谓的蒙提霍尔问题,实际上是来自于一个美国的电视游戏节目,这个结果的主持人就叫蒙提霍尔,因此才得此名。蒙提霍尔问题(这个电视结果的游戏规则)的描述如下。
观众面对三扇门,其中有一扇门的后面有一辆汽车,另外两扇后面各有一只山羊。游戏参与者可以从这三扇门中选择其中一扇,若选择的门后面是一辆汽车,则参赛者就可以赢得该汽车。一开始,当参赛者选定一扇门以后,主持人会从剩下的两扇门中打开其中一扇没有汽车的门(但是有山羊),然后问参赛者要不要更换自己的选择。这个问题的核心是参赛者更换自己的选择是否会增加自己获得汽车的概率?
首先,我们可以对这个问题进行一些基本分析。当参赛者选择一扇门以后,他所选定的这扇门没有汽车的概率是 ,其余两扇门有汽车的概率各为
。当主持人蒙提霍尔打开了一扇没有汽车的门以后,另外一扇没有被参赛者选中的门有汽车的概率变为
。所以,对参赛者而言,更改自己的选择可以使得获得汽车的概率从
提高到
,概率提高了一倍。综上分析,参赛者应该更换自己的选择。
下面,根据随机模拟的步骤解决这个问题。
首先,确定系统及系统的关键变量。
这个系统的输入是参赛者的选择,由于参赛者有两个策略{更换选择,不更换选择},犹豫者两个策略是互斥的,因此我们只需要模拟一个即可。根据提干,我们可以模拟当参赛者更换选择时其能获得汽车的概率。
其次,确定系统的运行规则。
由于参赛者是从三个门之间选择,且只有一扇门有车。因此,我们可以随机生成一个数 ,我们规定当
的时候表示参赛者选中了汽车。由于参赛者的策略
,所以当一开始
时,其最终结果为没选中,相反则参赛者最终获得汽车。
再次,对系统进行模拟运行。
采取更换选择策略,模拟的次数和最终能够获取到汽车的概率如下图所示。
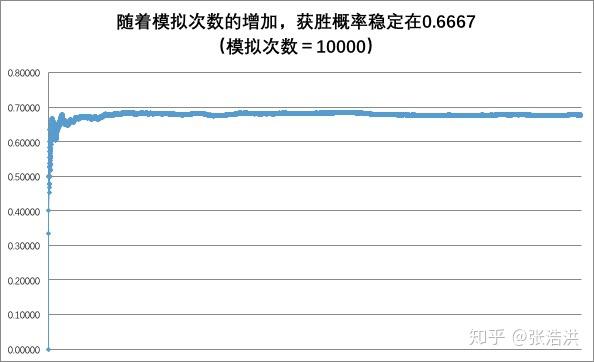
很明显,随着模拟次数的增加,参赛者在{更换选择}这个策略下获得汽车的概率稳定在0.667,也就是处。