随笔1-准确率函数

计算精度

函数原型
sklearn.metrics.precision_score(y_true, y_pred, labels=None, pos_label=1, average=’binary’, sample_weight=None)
函数注释
精度Precision=TP/(TP+FP)。其中TP是真正例，FP是假正例。精度直观地表示分类器标记正例的能力。最佳值为1，最差值为0

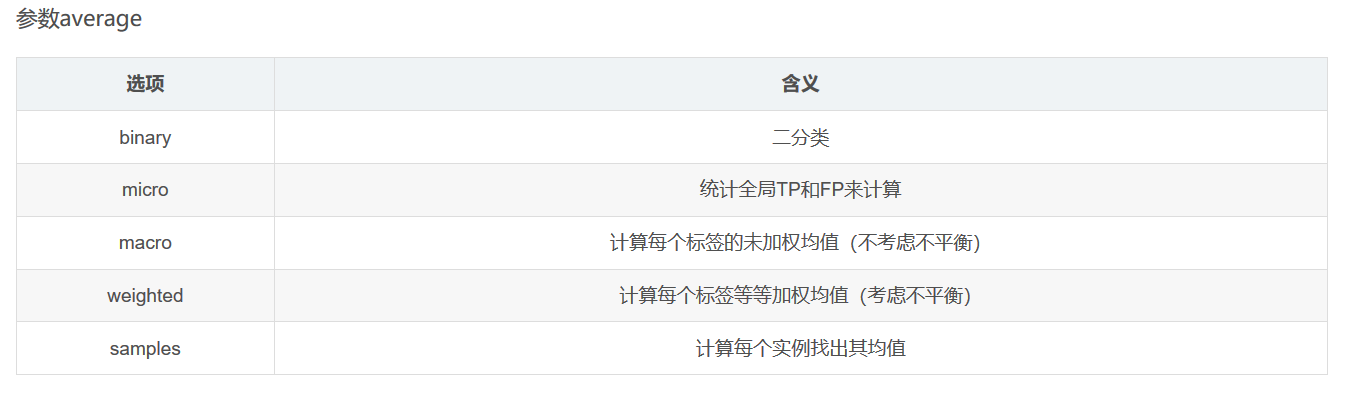
•  Macro Average（宏平均）

宏平均是指在计算均值时使每个类别具有相同的权重，最后结果是每个类别的指标的算术平均值。

• Micro Average（微平均）

微平均是指计算多分类指标时赋予所有类别的每个样本相同的权重，将所有样本合在一起计算各个指标。

• weighted

为每个标签计算指标，并通过各类占比找到它们的加权均值（每个标签的正例数）.它解决了’macro’的标签不平衡问题；它可以产生不在精确率和召回率之间的F-score.

• 如果每个类别的样本数量差不多，那么宏平均和微平均没有太大差异
• 如果每个类别的样本数量差异很大，那么注重样本量多的类时使用微平均，注重样本量少的类时使用宏平均
• 如果微平均大大低于宏平均，那么检查样本量多的类来确定指标表现差的原因
• 如果宏平均大大低于微平均，那么检查样本量少的类来确定指标表现差的原因

from sklearn.metrics import precision_score

y_true = [0, 1, 2, 0, 1, 2]

y_pred = [0, 2, 1, 0, 0, 1]

print(precision_score(y_true, y_pred, average='macro'))

# 0.2222222222222222

print(precision_score(y_true, y_pred, average='micro'))

# 0.3333333333333333

print(precision_score(y_true, y_pred, average='weighted'))

# 0.2222222222222222

print(precision_score(y_true, y_pred, average=None))

# [0.66666667 0. 0.]  #为三类个别的预测准确率，0.666667为0的预测准确率，0为1的预测准确率，0为2的预测准确率

参考：https://www.jianshu.com/p/6a80ef501882